链接:https://www.nowcoder.com/acm/contest/181/F
来源:牛客网
题目描述
给出一个长度为n的序列,你需要计算出所有长度为k的子序列中,除最大最小数之外所有数的乘积相乘的结果
输入描述:
第一行一个整数T,表示数据组数。
对于每组数据,第一行两个整数N,k,含义如题所示
接下来一行N个整数,表示给出的序列
保证序列内的数互不相同
输出描述:
对于每组数据,输出一个整数表示答案,对
取模
每组数据之间以换行分割
示例1
备注:
对于
的数据:
对于
的数据:
对于
的数据:
保证序列中的元素互不相同且
,
分析:

注意:ai的指数是一个非常大的数,不能直接进行快速幂计算,得先对这个指数进行降幂
考虑:欧拉降幂公式: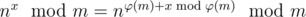 ,Φ(x)为欧拉函数
,Φ(x)为欧拉函数
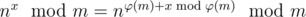 ,Φ(x)为欧拉函数
,Φ(x)为欧拉函数AC代码:
#include <map>
#include <set>
#include <stack>
#include <cmath>
#include <queue>
#include <cstdio>
#include <vector>
#include <string>
#include <bitset>
#include <cstring>
#include <iomanip>
#include <iostream>
#include <algorithm>
#define ls (r<<1)
#define rs (r<<1|1)
#define debug(a) cout << #a << " " << a << endl
using namespace std;
typedef long long ll;
const ll maxn = 1e3 + 10;
const double eps = 1e-8;
const ll mod = 1e9 + 7;
const ll inf = 1e9;
const double pi = acos(-1.0);
ll qow( ll a, ll b ) {
ll ans = 1;
while(b) {
if(b&1) {
ans = ans*a%mod;
}
a = a*a%mod;
b /= 2;
}
return ans;
}
ll c[maxn][maxn];
//两种欧拉函数求降幂数,第一种更快点
map<ll,ll> mp;
ll phi(ll k)
{
ll i,s=k,x=k;
if (mp.count(k)) return mp[x]; //记忆化存储
for(i = 2;i * i <= k; i++)
{
if(k % i == 0) s = s / i * (i - 1);
while(k % i == 0) k /= i;
}
if(k > 1) s = s / k * (k - 1);
mp[x]=s; return s;
}
ll eular( ll n ) {
ll ans = n;
for( ll i = 2; i*i <= n; i ++ ) {
if( n%i == 0 ) {
ans -= ans/i;
while( n%i == 0 ) {
n /= i;
}
}
}
if( n > 1 ) {
ans -= ans/n;
}
return ans;
}
int main() {
ll T;
scanf("%lld",&T);
//debug(eular(mod)); 利用欧拉函数求指数循环节,这里求得的是mod-1
memset(c,0,sizeof(c));
c[0][0] = 1;
for( ll i = 1; i <= 1000; i ++) {
for( ll j = 0; j <= i; j ++) {
if( j == 0 || j == i ) c[i][j] = 1;
else c[i][j] = ( c[i-1][j-1] + c[i-1][j] ) % (mod-1);
}
}
while( T -- ) {
ll n, m, a[maxn];
scanf("%lld%lld",&n,&m);
for( ll i = 1; i <= n; i ++ ) {
scanf("%lld",&a[i]);
}
sort(a+1,a+n+1);
ll ans = 1;
for( ll i = 1; i <= n; i ++ ) {
ll t = ((c[n-1][m-1]-c[i-1][m-1]-c[n-i][m-1])%(mod-1)+mod-1)%(mod-1);
ans = ans*qow(a[i],t)%mod;
}
printf("%lld
",ans);
}
return 0;
}