zoukankan      html  css  js  c++  java

  • ACM北大暑期课培训第五天

    　　今天讲的扫描线，树状数组，并查集还有前缀树。

    　　

    　　扫描线

      　扫描线的思路：使用一条垂直于X轴的直线，从左到右来扫描这个图形，明显，只有在碰到矩形的左边界或者右边界的时候，这个线段所扫描到的情况才会改变，所以把所有矩形的入边，出边按X值排序。然后根据X值从小到大去处理，就可以用线段树来维护扫描到的情况。

    　　如果碰到矩形的入边，就把这条边加入，如果碰到出边，就拿走。

    　　用根结点记录被覆盖的总长度     更新     

    　　插入数据的顺序：

    　　　　 将矩形的纵边从左到右排序，然后依次将这些纵边插入线段树。要记住哪些纵边是一个 矩形的左边(开始边)，哪些纵边是一个矩形 的右边（结束边），以便插入时，对Len（当前,本区间上有多长的 部分是落在那些矩形中的）和 Covers（本区间当前被多少个矩形 完全包含）做不同的修改。 插入一条边后,就根据根节点的Len 值增加总 覆盖面积的值。 增量是Len * 本边到下一条边的距离。  一开始，所有区间 Len = 0 Covers = 0

    　　扫描线和线段树推荐一个博客：https://www.cnblogs.com/AC-King/p/7789013.html 

    例题：POJ 1151 Atlantis

      1 #include <iostream>
  2 #include <algorithm>
  3 #include <math.h>
  4 #include <set>
  5 using namespace std;
  6 double y[210];
  7 struct CNode
  8 {
  9     int L,R;
 10     CNode * pLeft, * pRight;
 11     double Len; //当前,本区间上有多长的部分是落在那些矩形中的
 12     int Covers;//本区间当前被多少个矩形完全包含
 13 };
 14 CNode Tree[1000];
 15 struct CLine
 16 {
 17     double x,y1,y2;
 18     bool bLeft; //是否是矩形的左边
 19 } lines[210];
 20 int nNodeCount = 0;
 21 bool operator< ( const CLine & l1,const CLine & l2)
 22 {
 23     return l1.x < l2.x;
 24 }
 25 template <class F,class T>
 26 F bin_search(F s, F e, T val)
 27 {
 28     //在区间[s,e)中查找 val,找不到就返回 e
 29     F L = s;
 30     F R = e-1;
 31     while(L <= R )
 32     {
 33         F mid = L + (R-L)/2;
 34         if( !( * mid < val || val < * mid ))
 35             return mid;
 36         else if(val < * mid)
 37             R = mid - 1;
 38         else
 39             L = mid + 1;
 40     }
 41     return e;
 42 }
 43 int Mid(CNode * pRoot)
 44 {
 45     return (pRoot->L + pRoot->R ) >>1;
 46 }
 47 void Insert(CNode * pRoot,int L, int R)
 48 //在区间pRoot 插入矩形左边的一部分或全部，该左边的一部分或全部覆盖了区间[L,R]
 49 {
 50     if( pRoot->L == L && pRoot->R == R)
 51     {
 52         pRoot->Len = y[R+1] - y[L];
 53         pRoot->Covers ++;
 54         return;
 55     }
 56     if( R <= Mid(pRoot))
 57         Insert(pRoot->pLeft,L,R);
 58     else if( L >= Mid(pRoot)+1)
 59         Insert(pRoot->pRight,L,R);
 60     else
 61     {
 62         Insert(pRoot->pLeft,L,Mid(pRoot));
 63         Insert(pRoot->pRight,Mid(pRoot)+1,R);
 64     }
 65     if( pRoot->Covers == 0) //如果不为0，则说明本区间当前仍然被某个矩形完全包含，则不能更新 Len
 66         pRoot->Len = pRoot->pLeft ->Len + pRoot->pRight ->Len;
 67 }
 68 void Delete(CNode * pRoot,int L, int R)
 69 {
 70 //在区间pRoot 删除矩形右边的一部分或全部，该矩形右边的一部分或全部覆盖了区间[L,R]
 71     if( pRoot->L == L && pRoot->R == R)
 72     {
 73         pRoot->Covers --;
 74         if( pRoot->Covers == 0 )
 75             if( pRoot->L == pRoot->R )
 76                 pRoot->Len = 0;
 77             else
 78                 pRoot->Len = pRoot->pLeft ->Len + pRoot->pRight ->Len;
 79         return ;
 80     }
 81     if( R <= Mid(pRoot))
 82         Delete(pRoot->pLeft,L,R);
 83     else if( L >= Mid(pRoot)+1)
 84         Delete(pRoot->pRight,L,R);
 85     else
 86     {
 87         Delete(pRoot->pLeft,L,Mid(pRoot));
 88         Delete(pRoot->pRight,Mid(pRoot)+1,R);
 89     }
 90     if( pRoot->Covers == 0) //如果不为0，则说明本区间当前仍然被某个矩形完全包含，则不能更新 Len
 91         pRoot->Len = pRoot->pLeft ->Len + pRoot->pRight ->Len;
 92 }
 93 void BuildTree( CNode * pRoot, int L,int R)
 94 {
 95     pRoot->L = L;
 96     pRoot->R = R;
 97     pRoot->Covers = 0;
 98     pRoot->Len = 0;
 99     if( L == R)
100         return;
101     nNodeCount ++;
102     pRoot->pLeft = Tree + nNodeCount;
103     nNodeCount ++;
104     pRoot->pRight = Tree + nNodeCount;
105     BuildTree( pRoot->pLeft,L,(L+R)/2);
106     BuildTree( pRoot->pRight,(L+R)/2+1,R);
107 }
108 int main()
109 {
110     int n;
111     int i,j,k;
112     double x1,y1,x2,y2;
113     int yc,lc;
114     int nCount = 0;
115     int t = 0;
116     while(true)
117     {
118         scanf("%d",&n);
119         if( n == 0) break;
120         t ++;
121         yc = lc = 0;
122         for( i = 0; i < n; i ++ )
123         {
124             scanf("%lf%lf%lf%lf", &x1, &y1,&x2,&y2);
125             y[yc++] = y1;
126             y[yc++] = y2;
127             lines[lc].x = x1;
128             lines[lc].y1 = y1;
129             lines[lc].y2 = y2;
130             lines[lc].bLeft = true;
131             lc ++;
132             lines[lc].x = x2;
133             lines[lc].y1 = y1;
134             lines[lc].y2 = y2;
135             lines[lc].bLeft = false;
136             lc ++;
137         }
138         sort(y,y + yc);
139         yc = unique(y,y+yc) - y;
140         nNodeCount = 0;
141 //yc 是横线的条数，yc- 1是纵向区间的个数，这些区间从0
142 //开始编号，那么最后一个区间
143 //编号就是yc - 1 -1
144         BuildTree(Tree, 0, yc - 1 - 1);
145         sort(lines,lines + lc);
146         double Area = 0;
147         for( i = 0; i < lc - 1 ; i ++ )
148         {
149             int L = bin_search( y,y+yc,lines[i].y1) - y;
150             int R = bin_search( y,y+yc,lines[i].y2) - y;
151             if( lines[i].bLeft )
152                 Insert(Tree,L,R-1);
153             else
154                 Delete(Tree,L,R-1);
155             Area += Tree[0].Len * (lines[i+1].x - lines[i].x);
156         }
157         printf("Test case #%d
",t);
158         printf("Total explored area: %.2lf
",Area);
159         printf("
",Area);
160     }
161     return 0;
162 }
    老师上课讲的代码

    　　树状数组

    　　只能解决单点更新、区间求和问题。

    　　可以快速求出任意区间和。

    　　能力比线段树弱。  它能解决的问题线段树都能解决，是线段树能解决的问题的子集。

    　　它的好处： 1.写起来简单    2.效率高（常数小）        ps:线段树常数大       两者区间查询的时间复杂度都是O(logn）

    　　三个重要的函数 ： 

    int lowerbit(int x)
{
    return x&-x;
}

void Update(int i,int v)  // 初始化与单点修改 
{
    while(i <= n)
    {
        c[i] += v ;
        i += lowbit(i) ;
    }
}

int Sum(int i)   // 区间求和 
{
    int res = 0 ;
    while(i)
    {
        res += c[i] ;
        i -= lowbit(i) ;
    }
    return res ;
}

    　　

    　　lowbit(x)： 只保留x的二进制最右边的1，其余位都变为0后的值  

    　　对于序列a，我们设一个数组C   C[i] = a[i – 2 k + 1] + … + a[i]   C即为a的树状数组

    　　k为i在二进制下末尾0的个数    2k就是i 保留最右边的1，其余位全变0  

    　　 i从1开始算！

    　　

    　　C[i] = a[i-lowbit(i)+1] + …+ a[i] C包含哪些项看上去没有规律 

    　　C1=A1

    　　C2=A1+A2

    　　C3=A3

    　　C4=A1+A2+A3+A4

    　　C5=A5

    　　C6=A5+A6

    　　C7=A7

    　　C8=A1+A2+A3+A4+A5+A6+A7+A8 

    　　 …………

    　　C16=A1+A2+A3+A4+A5+A6+A7+A8+A9+A10+ A11+A12+A13+A14+A15+A16

    　　树状数组图示 

     

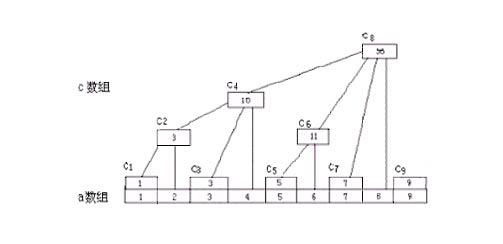
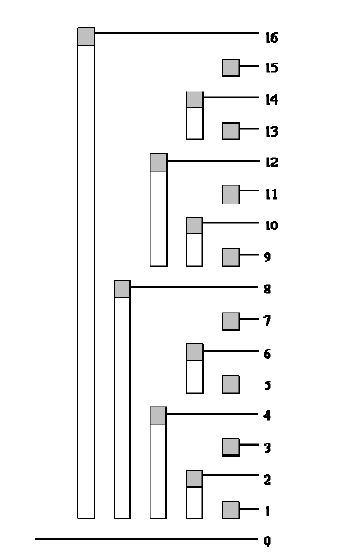
    　　将C[]数组的结点序号转化为二进制

    　　1=(001)      C[1]=A[1];
    　　2=(010)      C[2]=A[1]+A[2];
    　　3=(011)      C[3]=A[3];
    　　4=(100)      C[4]=A[1]+A[2]+A[3]+A[4];
    　　5=(101)      C[5]=A[5];
    　　6=(110)      C[6]=A[5]+A[6];
    　　7=(111)      C[7]=A[7];
    　　8=(1000)    C[8]=A[1]+A[2]+A[3]+A[4]+A[5]+A[6]+A[7]+A[8];
    　　对照式子可以发现  C[i]=A[i-2^k+1]+A[i-2^k+2]+......A[i]; （k为i的二进制中从最低位到高位连续零的长度）

     　　时间复杂度：建数组： O(n) 更新： O(logn) 局部求和：O(logn)

    　　树状数组推荐博客：https://www.cnblogs.com/ECJTUACM-873284962/p/6380245.html

    　　POJ题目推荐： 2182, 2352, 1177, 3667,3067

     　　并查集

     　　3个操作：

    　　1.合并两个集合

    　　2.查询一个元素在哪个集合

    　　3.查询两个元素是否属于同一集合

    　　核心：查一个元素的树根（时间复杂度为常数）

    　　实际应用代码：

     1 int par[];
 2 int GET_ROOT(int a)//查询一个元素在哪个集合  路径压缩
 3 {
 4     if (par[a]!=a)
 5         par[a] = GET_ROOT(par[a]);
 6     return par[a];
 7 }
 8 int query(int a,int b)//查询两个元素是否属于同一集合 
 9 {
10     return GET_ROOT(a)==GET_ROOT(b);
11 }
12 void merge(int a,int b)//合并两个集合
13 {
14     par[GET_ROOT(a)] = GET_ROOT(b);
15 }

    　　有时候需要添加数组记录，例如添加sum数组记录每个集合有多少元素。

    　　在合并时进行维护 

    　　做题时主要理清怎样算同一集合。

    例题：1.POJ 1611 The Suspects

    　　　2.POJ 1988 Cube Stacking

    　　　3.POJ 1182 食物链

    　　DFA（一部分）

     　   多模式匹配

    　　trie图是一种DFA，可以由trie树为基础构造出来， 对于插入的每个模式串，其插入过程中使用的最后一 个节点都作为DFA的一个终止节点。 如果要求一个母串包含哪些模式串，以用母串作为 DFA的输入，在DFA 上行走，走到终止节点，就意 味着匹配了相应的模式串(没能走到终止节点，并不 意味着一定不包含模式串)。

    　　避免母串指针回溯  -->  记住哪些模式串的哪个前缀已经被匹配  -->前缀指针 

    　　前缀指针：仿照KMP算法的Next数组， 我们也对树上的每一个节点 建立一个前缀指针。这个前 缀指针的定义和KMP算法中 的next数组相类似，从根节 点沿边到节点p我们可以得 到一个字符串S，节点p的前 缀指针定义为：指向树中出 现过的S的最长的后缀(不能等于S)。
  • 相关阅读:
    分布式缓存HttpRuntime.cache应用到单点登陆中_优化登陆
    ID Codes
    Smith Numbers经典
    青蛙的约会
    exp_euler两种形式int,void(扩展欧几里得算法)可求最大公约数，二元一次方程的解
    A/B
    Raising Modulo Numbers
    Brave balloonists 求素因子的个数
    排列
    Anagram
  • 原文地址：https://www.cnblogs.com/l999q/p/9379619.html
Copyright © 2011-2022 走看看