今天学了有流量下界的网络最大流,最小费用最大流,计算几何。
有流量下界的网络最大流
如果流网络中每条边e对应两个数字B(e)和C(e), 分别表示该边上的流量至少要是B(e),最多 C(e),那么,在这样的流网络上求最大流,就是有下界的最大流问题。
这种网络不一定存在可行流
思路:将下界“分离”出去,使问题转换为下界为0的普通网络流问题。
将原弧(u,v)分离出一条必要弧和一条非必要弧:
假设B(u,v)是下界,则分离出两条弧: C1(u,v) = B(u,v) -- 必要弧
C2(u,v) = C(u,v) – B(u,v)
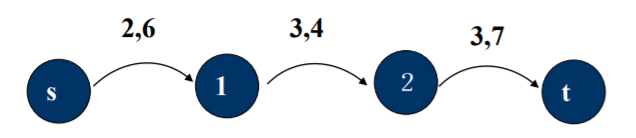
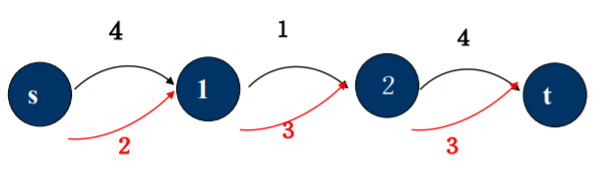
由于必要弧的有一定要满流的限制,将必要弧“拉” 出来集中考虑
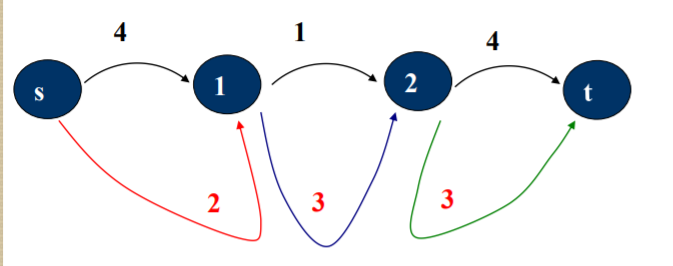
添加附加点x,y。想像一条不限上界的(x, y),用必要弧将它们“串”起来,即对于有向必要弧(u, v),添加 (u, x),(y, v),容量为必要弧容量。这样就建立了一个等价的网络。
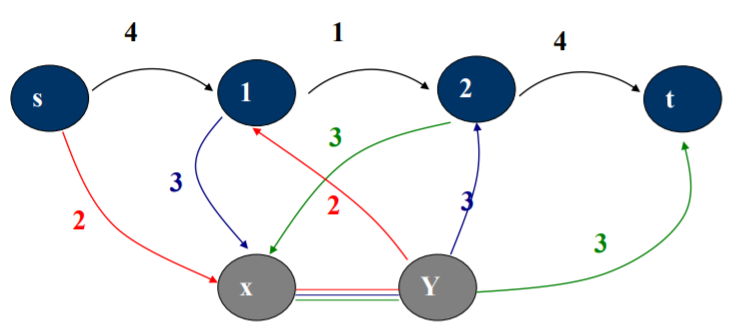
去掉边(x,y),添加由t到s的容量为正无穷大的边,使y和 x分别成为新的源和新的汇。
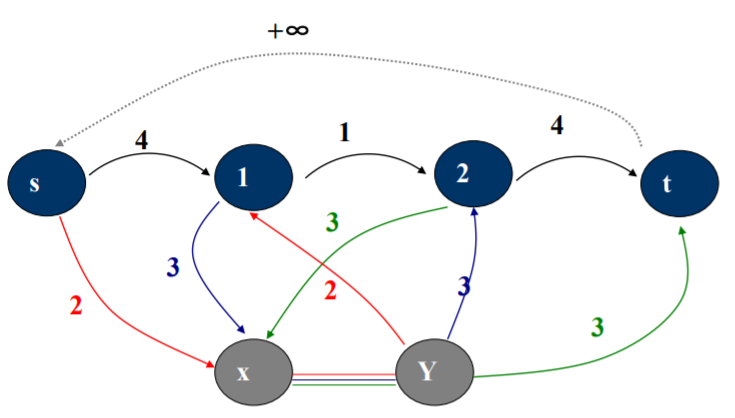
若此图上的最大流能够占满与Y相连的所有边的容量(自 然也就会占满所有连到x的边的容量),那么原图上就存 在满足上下界条件的可行流。若最大流不能够占满与Y相 连的所有边的容量,则原图不存在可行流。
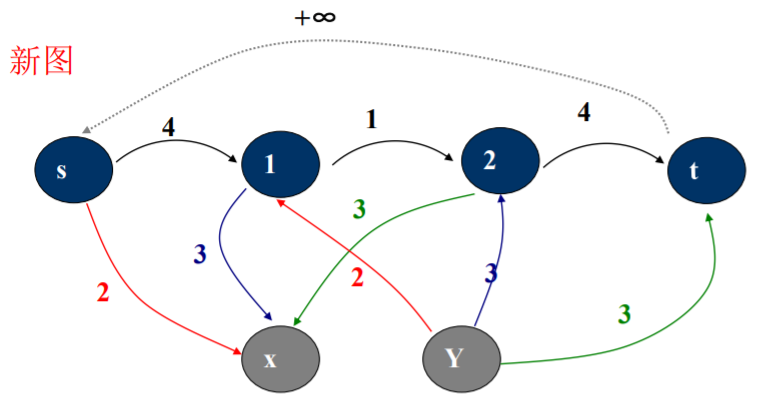
新图最大流若小于新图中x的流入量之和,则原问题 无解
在新图的最大流中,求出s流出的流量之和,记为 sum1
在做过一遍最大流的新图的残余网络中,去掉t->s 以及s->t的边,然后以s为源,t为汇再做一次最大流, 此时得到的流量 sum2,则 sum1+sum2就是在原图 上满足下界的最大流。
和x,y相连的边不用处理,因为x,y实际上是只能流入 或只能流出的点,在图中不起作用。
要想求出每条边上的流量,怎么办?
在做第二次最大流之前,将图备份到G2
经过两次求最大流后,最后变成的残余网络是G
此时G2[i][j] – G[i][j] + LC[i][j] 就是 i->j上的流量
LC[i][j] 是i->j边上的流量下界(下界是被满足的)
处理网络流题目要注意,如果有重边,则要将重边 上的容量和下界累加,合并成一条边。
例题:POj 2396 Budget

题目: 现在有一个n*m的方阵,方阵里面的数字未知,但是我们知道如下约束条件: 1> 每一行的数字的和 2> 每一列的数字的和 3> 某些格子里的数,大小有限制。比如规定第2 行第3列的数字必须大于5(或必须小于3,或必须等于10等) 求解是否存在在满足所有的约束的条件下用正数来填充该方阵的方案,若有,输出填充后的方阵,否则输出IMPOSSIBLE. 这道题可以转化成容量有上下界的最大流问题,将方阵的行从1……n编号,列n+1……n+m编号,添加源点s=0和汇点t=n+m+1. 1>将源点和每一个行节点相连,相连所形成的边的容量和下界置为该行所有数字的和 2>将每一个列节点和汇点相连,相连所形成的边的容量和下界都置为该列所有数字的和 3>从每个行节点到每个列节点连边,容量为无穷大 4> 如果u行v列的数字必须大于w,则边<u,v+n>流量的下界是w+1 5> 如果u行v列的数字必须小于w,则边<u,v+n>容量改为w-1 6> 如果u行v列的数字必须等于w,则边<u,v+n>流量的下界和容量都是w找到的可行流(也是最大流),就是问题的解 本题trick: 1) W可能为负数,产生流量下界为负数的情况。应处理成0 2) 数据本身可能矛盾。比如前面说了 (2,1) =1,后面又说(2,1) = 10
最小费用最大流
以下内容引自http://web.nuist.edu.cn/courses/dlxxxt/ch5/5.7.3.htm
http://jpkc.lzjtu.edu.cn/material3/xxxt/zxfyzdl.htm
设有一个网络图G(V,E),,V={s,a,b,c,…,s’},E中 的每条边(i,j)对应一个容量c(i,j)与输送单位流量所需费用 a(i,j)。如有一个运输方案(可行流),流量为f(i,j),则 最小费用最大流问题就是这样一个求极值问题: 其中F为G的最大流的集合,即在最大流中寻找一个费用 最小的最大流。
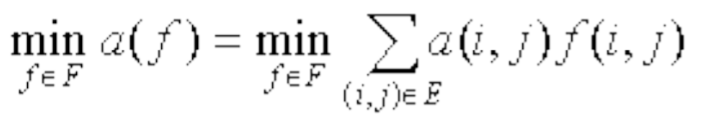

反复用spfa算法做源到汇的最短路进行增广,边权值为边上单位费用。反向边上的单位费用是负的。
直到无法增广,即为找到最小费用最大流。
成立原因:每次增广时,每增加1个流量,所增加的费用都是最小的。 (最短路) (最小费用==>路径长度总和)
因为有负权边(取消流的时候产生的),所以不能用迪杰斯特拉算法求最短路。(用SPFA)
二分图最大匹配(网络流问题)
计算几何
基础——点、线、面
解析几何:列方程,解方程 (麻烦,特殊情况太多)
计算几何:1.表示简单
2.功能强大
3.特殊情况少,思维难度较低
4.函数可重复利用(即所谓的“模版”)
5.尽可能避免除法和三角函数,精度高,效率高

1 struct CVector///矢量表示 2 { 3 double x, y; 4 }; 5 ///表示从0点到 (x,y)的矢量。对矢量只关心方向 6 ///和长度,不关心(位置)起点终点 7 8 ///矢量的基本运算 9 CVector operator + (CVector p, CVector q)///矢量和 10 { 11 return CVector(p.x + q.x, p.y + q.y); 12 } 13 14 CVector operator -(CVector p, CVector q) 15 { 16 return CVector(p.x - q.x, p.y - q.y); 17 } 18 19 CVector operator *(double k, CVector p) 20 { 21 return CVector(k * p.x, k * p.y); 22 } 23 24 ///矢量的点积 25 ///性质:p·q=|p||q|cos<p,q> 26 ///a与b的点积,就是a的模乘以b在a上投影的模。若投影与a方向相反则为负值 27 ///其值的正负表示方向 28 ///功能:求同向还是异向;求投影;求出投影后用勾股定理求点到直线距离; 29 ///若a * b = 0,则 a和b垂直 30 double operator *(CVector p, CVector q) 31 { 32 return p.x * q.x + p.y * q.y; 33 } 34 35 ///矢量模长 36 ///用矢量与自身点积求模 37 double length(CVector p)///求矢量的模 38 { 39 return sqrt(p * p); 40 } 41 42 ///矢量单位化 43 ///将矢量除以自身的长度以得到同方向的单位矢量 44 CVector unit(CVector p) 45 { 46 return 1 / length(p) * p; 47 } 48 49 ///矢量的投影长度 50 ///矢量与该方向单位矢量的点积 51 ///注意:负数表示反方向 52 double project(CVector p, CVector n)///点积 53 { 54 return dot(p, unit(n)); 55 } 56 double dot(CVector p, CVector q) 57 { 58 return p.x*q.x+p.y*q.y; 59 } 60 61 ///矢量的叉积 62 ///性质:在二维情况中,|p×q|=|p||q|sin<p,q> 63 ///功能:求面积;求顺时针方向还是逆时针方向;判断是否在半平面上 64 ///用法:c = a ^ b; //a,b,c都是CVector对象 65 ///a×b 为有向面积,可正可负。 66 ///若a逆时针旋转小于180度可到b,则结果为正,否则结果为负 67 double operator ^(CVector p, CVector q) 68 { 69 return p.x * q.y – q.x * p.y; 70 } 71 72 ///两个矢量所围成的三角形的面积 73 ///两个矢量的叉积的一半 74 ///注意:得到的面积为有向面积,可能为负 75 double area(CVector p, CVector q) 76 { 77 return p^q / 2; 78 }
矢量的点积:
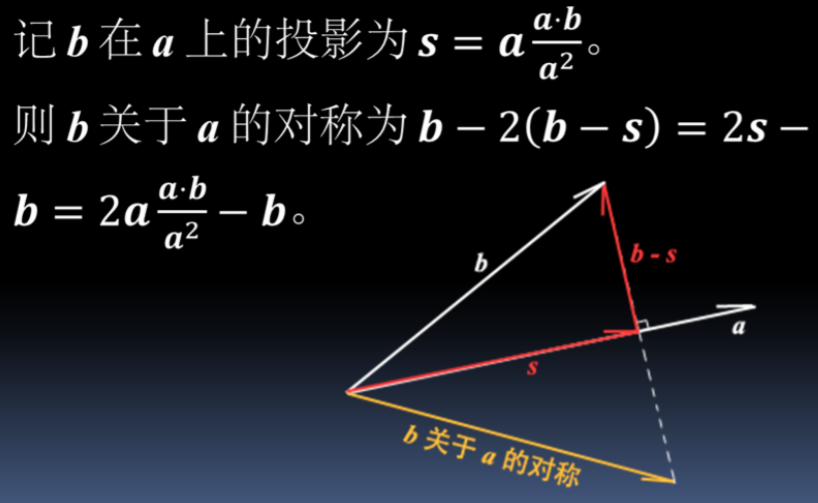
未完...
