「一本通 1.3 例 5」weight]

「一本通 1.3 例 5」weight

题面

给定原数列 (a_1,a_2,a_n) ,给定每个数的前缀和以及后缀和，并且打乱顺序。

给出一个集合 (S) 要求从集合 (S) 中找到合适的数，满足给定的所有数例前缀和和后缀和，答案保证最小的

思路

很多人上来没有思路，不知从何搜起

• 简单讲就是找到正确的搜索顺序，往里面放数就好了

  他不是有前缀和也有后缀和嘛~，而且还是混着的，

  那么你就直接排序，然后安排两个指针 (L) 和 (R) 的表示左边和右边，

  记录每个 (L) 的前缀和 和 (R) 的后缀和，然后用当前的你所枚举的（题中给出的混杂数列）(A[k]) 相减，即 (A[k] - Sum[L] 或者 A[k] - Sum[r]) ，

  只要相减的差在给定集合 (S) 里，直接搜索下一层，两个指针肯定会跑到一起，最后再判断答案合不合限定范围就可以了 (Over)

-----------------------------------------------------------------------分割线----------------------------

• 详细的说 就是通过给定的条件，找到约束条件，进而说明我为什么要选择上面的搜索顺序和思路

  • 令 满足要求的 (SumL_i) （原数列 (N),右同），表示位置 (i) 的前缀和 ，
  • 令 满足要求的 (SumL_j) 表示位置 (j) 的后缀和，
  • 令 (ans_i) 为答案数列

  不难发现

  可以将打乱的先排序，最后的数(Max)显然就是 (SumL_n) 和 (SumR_n), 最小的数 (Min) 要不是最左边，要不是最右边。(剪枝1)

• 我们从已知条件的数据当中任意取出两个数的时候，只会出现以下两种情况：

• 

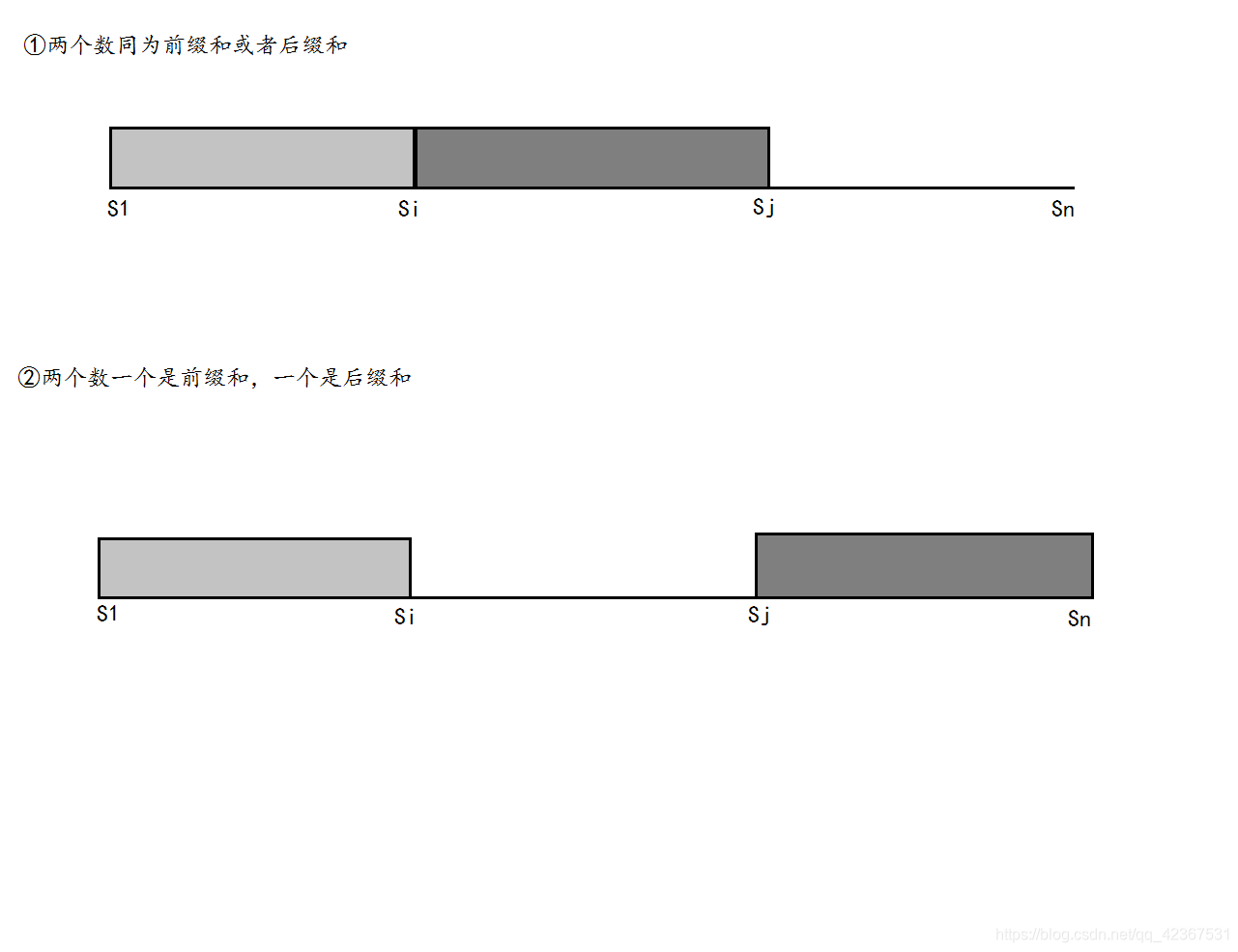
• 当为一种情况时，即都为前缀和或后缀和(后面的前缀和和后缀和统一用 (Sum) 表示，以为我说的是第一种情况)，

• 那么 (Sum_{i+1} - Sum_i) 就是位置 (i) 的 (ans[i]) ，所以我们找到了达成要求的条件，即知道满足 两个(A[k] - A[p] （k,p均为变量）) 的差值在集合 (S) 中，那么就找到了当前正确的 (Sum_i)

• 凭着是上面的条件，我们可以将枚举 (A[k]) ，并放入相应的位置中，那么他放的可能无非就两种，一是放在左边，二是放在右边，那么枚举时记录一下左右当前位置 (L) 和 (R) （即在 (L-R) 范围内都是还没填上数的），一直搜到 (L == R) ，输出就行，（因为开始我先进行了排序，所以找到的答案一定为最小序列的）

终于说完了~累死了

Code

#include <iostream>
#include <cstdio>
#include <cmath>
#include <algorithm>
#include <queue>
using namespace std;
//#define int long long
const int manx = 1e7;
const int maxm = 1e8;
const int inf = 0x3f3f3f3f;
int read(){
	char c = getchar();int x = 0,f = 1;
	for( ;!isdigit(c);c = getchar()) if(c == '-') f = -1;
	for( ;isdigit(c);c = getchar()) x = x * 10 + (c ^ 48);
	return x * f;
} 
int a[manx],ans[manx];
bool vis[manx],flag;
int n, m, i;
void dfs(int k ,int l ,int r ,int sum_l ,int sum_r){
	/*
	 k 表示枚举的数据给出的已经排完序的A[k]
	 l,r 表示搜到的左右边界（l,r是我们要填数的其中一个，所以记录的都是他们前一个或后一个的和），
	 sum_l,sum_r 分别记录的是l-1的前缀和,r+1的后缀和,
	*/
    if(flag == true) return;//完成深搜
	if(l == r){
		if(vis[a[k] - sum_l] == false && vis[a[k] - sum_r] == false) return;
		if( a[2 * n] - sum_l - sum_r < 1 || a[2 * n] - sum_l - sum_r > 500) return; //这里被卡，防止在加数的先选的大的，剩下个小的，之后一相减就成负数了
		ans[l] = a[2 * n] - sum_l - sum_r;
		for(i = 1;i <= n; i++) printf("%d ",ans[i]);
		cout<<'
';
		flag = true;
	}
	if(vis[a[k] - sum_l] == true ){
		ans[l] = a[k] - sum_l;
		dfs(k + 1 ,l + 1 ,r ,a[k] ,sum_r);
	}
	if(vis[a[k] - sum_r] == true ){
		ans[r] = a[k] - sum_r;
		dfs(k + 1 ,l , r - 1,sum_l , a[k]);
	}
	
}
int main(){
	//freopen("dd.in","r",stdin);
	//freopen("dd.out","w",stdout); 
	n = read();
	for(i = 1;i <= n * 2;i ++) a[i] = read(); 
	sort(a + 1 ,a + 1 + n * 2);
	m = read();
	for(i = 1;i <= m; i++) {
		int x = read();
		vis[x] = true;//表示x这数在不在集合S当中
	}
	dfs(1,1,n,0,0);
	return 0;
}

最累的题解了~