“浪潮杯”第九届山东省ACM大学生程序设计竞赛 F: Four-tuples容斥定理

题目

F : Four-tuples

 输入

1
1 1 2 2 3 3 4 4

输出

1

---

题意

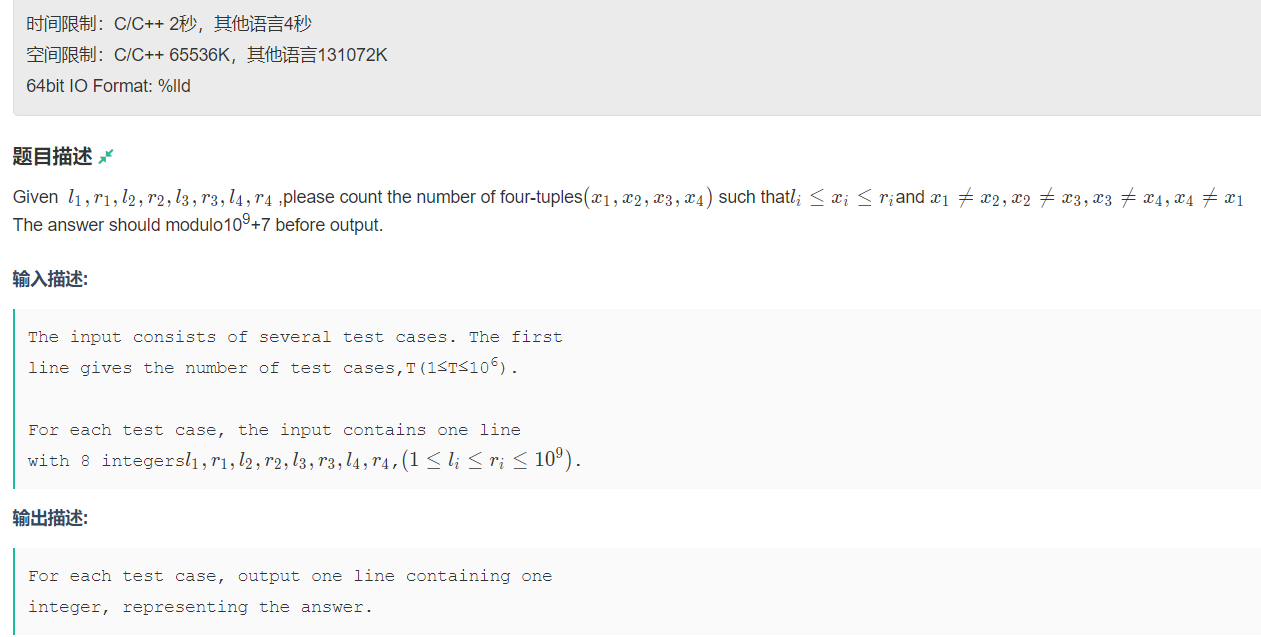
给l₁, r₁, l₂, r₂, l₃, r₃,  l₄, r_4​ , 八个数据, 要求输出在区间[l₁, r₁] ,  [l₂, r₂] , [l₃, r₃] ,  [l₄, r_4​]

(记为A, B, C, D)范围内, 各取一个数(取作x1, x2, x3, x4), 并且x1 != x2, x2 != x3, x3 != x4, x4 != x1,

 注意像x1 == x3是可以的

思路

容斥原理 

结果 = 每个区间值的个数相乘 - 四种相等的情况即x1=x2, x2=x3...... (前者好说, 关键是后面这部分)

 

四种相等的情况计算方法:(ABCD代表四个区间里的任意一个数)

 

 

---

AC代码

#include <bits/stdc++.h>
#include <algorithm>

using namespace std;

const int mod = 1e9 + 7;

typedef long long ll;

ll query2(ll l1, ll r1, ll l2, ll r2)//query求的是几个区间重复的数的个数, 以下也是
{
    ll l = max(l1, l2), r = min(r1, r2);
    return r-l+1>0? r-l+1 : 0;
}
ll query3(ll l1, ll r1, ll l2, ll r2, ll l3, ll r3)
{
    ll l = max(l1, max(l2, l3)), r = min(r1, min(r2, r3));
    return r-l+1>0? r-l+1 : 0;
}
ll query4(ll l1, ll r1, ll l2, ll r2, ll l3, ll r3, ll l4, ll r4)
{
    ll l = max(max(l3, l4), max(l1, l2)), r = min(min(r3, r4), min(r1, r2));
    return r-l+1>0? r-l+1 : 0;
}

int main()
{
    int t;
    ll l1, l2, l3, l4, r1, r2, r3, r4;
    cin >> t;
    while( t --)
    {
        scanf("%lld%lld%lld%lld%lld%lld%lld%lld", &l1,&r1,&l2,&r2,&l3,&r3,&l4,&r4); 
        
        ll len1 = r1 - l1 + 1;
        ll len2 = r2 - l2 + 1;
        ll len3 = r3 - l3 + 1;
        ll len4 = r4 - l4 + 1;
        
        ll sum = len1 * len2 % mod;
        sum = sum * len3 % mod; 
        sum = sum * len4 % mod;
        
        ll ant = 0;
        ant = (ant + query2(l1, r1, l2, r2) % mod * len3  % mod * len4 % mod) % mod;
        ant = (ant + query2(l2, r2, l3, r3) % mod * len1  % mod * len4 % mod) % mod;
        ant = (ant + query2(l4, r4, l3, r3) % mod * len1  % mod * len2 % mod) % mod;
        ant = (ant + query2(l4, r4, l1, r1) % mod * len2  % mod * len3 % mod) % mod;
    // 第一步完成---------------------------------------------------------
        
        ant = (ant - query3(l1, r1, l2, r2, l3, r3) % mod * len4 % mod + mod) % mod;
        ant = (ant - query3(l1, r1, l2, r2, l4, r4) % mod * len3 % mod + mod) % mod;
        ant = (ant - query3(l4, r4, l2, r2, l3, r3) % mod * len1 % mod + mod) % mod;
        ant = (ant - query3(l1, r1, l4, r4, l3, r3) % mod * len2 % mod + mod) % mod;
    // 第二步完成---------------------------------------------------------
        
        ant = (ant - query2(l1, r1, l2, r2) % mod * query2(l4, r4, l3, r3) % mod  + mod) % mod;
        ant = (ant - query2(l2, r2, l3, r3) % mod * query2(l4, r4, l1, r1) % mod + mod) % mod;
    // 第三步完成---------------------------------------------------------
         
        ant = (ant + 3 * query4(l1, r1, l2, r2, l3, r3, l4, r4) % mod + mod) % mod;
    // 第四步完成---------------------------------------------------------
     
        cout << (sum - ant + mod) % mod << endl;
    }
    
    return 0;
}