http://poj.org/problem?id=1905
题意:已知一根线的长度L,受温度影响膨胀后的弧长s = (1+n*c)*L,求膨胀后与膨胀前的最大距离h。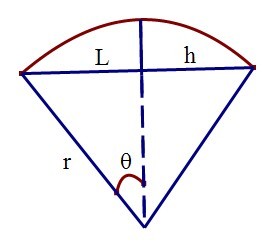
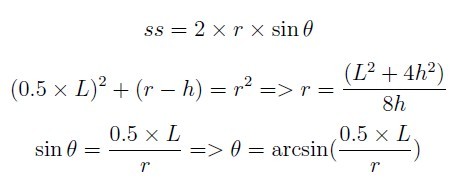
思路:二分枚举h,通过推出的公式算出ss,不断改变h的上下界,使ss不断接近s,因为数据为double型,比较时应注意精度问题。修改:(上式应为(r-h)^2)

1 #include <stdio.h> 2 #include <math.h> 3 const double eps=1e-8; 4 int main() 5 { 6 double L,c,n; 7 while(~scanf("%lf%lf%lf",&L,&c,&n)) 8 { 9 if (L==-1&&c==-1&&n==-1) 10 break; 11 double low = 0,high = 0.5*L,mid; 12 double s = (1+n*c)*L;//已知的弧长 13 while(high-low > eps) 14 { 15 mid = (high+low)/2; 16 double r = (L*L+4*mid*mid)/(8*mid);//半径 17 double ss = 2*r*asin(((0.5*L)/r));//此时的弧长 18 if (ss < s)//ss < s 说明h的范围应在[mid,high]; 19 low = mid; 20 else 21 high = mid;//此时h的范围为[low,mid] 22 } 23 printf("%.3f ",mid); 24 } 25 return 0; 26 }
