LeetCode Sqrt

    int sqrt(int x) {
        int lo = 0;
        int hi = x;
        int m = 0;
        double mul = 0;
        for (;;) {
            m = (lo + hi) / 2;
            if (lo > hi) break;
            mul = 1.0 * m * m;
            if (mul > x) {
                hi = m - 1;
            } else if (mul == x) {
                break;
            } else {
                lo = m + 1;
            }
        }
        return m;
    }

变量mul使用了double类型防止溢出（至少不会折回），因为依据IEEE754标准double类型能够精确表示的连续整数范围是[-2^53, 2^53]，虽然double类型在表示浮点数时有误差，但是如果保证所有的操作都是整数（加一个整数，减一个整数，乘一个整数，除一个约数）的，那么结果依然是一个精确的整数（在不超范围的情况下），那么递推的后续的操作都是可靠的。

本题中当x是一个超大的数时如INT_MAX时，尝试得到的mul可能会超出long类型的表示范围（可以用long long），但此时我们不需要知道它的确切值，因为它肯定不是x的一个根（mul>x）。因为double可以精确表示的范围已经包含int类型的范围，当mul接近x时（m接近x的根），进行等值判断（mul == x）就是可靠的。

虽然浮点数的判断问题有时确实让人烦恼，尤其是图形学的算法中，但是可靠不可靠还是要根据具体场景来进行判断的。

另外除了二分法还有牛顿切线法（迭代式如下，对于求n的平方根，f(x)=x^2 - n, f'(x)=2x）

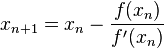
    int sqrt(int x) {
        if (x == 0) return 0;
        double i = x;
        int last;
        for(;;) {
            last = i;
            i = i - i/2.0 + x/2.0/i;
            if ((int)i == last) break;
        }
        return last;
    }

还有其他一些古怪的方法来求浮点数的根。 

参考：

IEEE754 介绍 http://blog.csdn.net/seizef/article/details/5571783

牛顿法 http://zh.wikipedia.org/wiki/%E7%89%9B%E9%A1%BF%E6%B3%95