作者
Hongyi Zhang 张宏毅 @ 张宏毅知乎 北大->MIT 论文所属FAIR
Abstract
深度神经网络有些不好的行为:强记忆和对对抗样本敏感
Christian Szegedy等人在ICLR2014发表的论文中,他们提出了对抗样本(Adversarial examples)的概念,即在数据集中通过故意添加细微的干扰所形成的输入样本,受干扰之后的输入导致模型以高置信度给出一个错误的输出。在他们的论文中,他们发现包括卷积神经网络(Convolutional Neural Network, CNN)在内的深度学习模型对于对抗样本都具有极高的脆弱性。
提出了mixup这个方法来减轻这些问题, mixup是在样本对以及标签对的凸组合上进行训练。
在ImageNet2012,CIFAR10/100,UCI,Google commands都取得了更好的结果,也就是说提高了当前最好的网络模型的泛化性能
Introduction
神经网络有两个共性: 使用ERM(最小化所有训练数据的平均误差) + 对应不同数据集的最优模型的大小(参数量表示)和数据集数据量是同步线性增长关系

Vapnik & Chervonenkis, 1971 经典的学习理论: ERM的收敛性可以得到保证,只要模型的大小(参数量或者VC复杂度)不睡训练数据的增长而增长
这与上面的现象矛盾,那么ERM真的是合理的吗?一方面,ERM使得神经网络强记训练数据(而不是泛化)甚至对数据进行任意的标签赋值,另一方面,ERM对于对抗样本非常敏感,与训练数据集分布稍微不一样,就会得到大不同的结果
ERM没有能力解释或者提供 在与训练集分布稍微不同的数据上的泛化能力.
数据增广, 形式化为VRM(Vicinal Risk Minimization)领域风险最小化,已证明数据增广可以提升泛化性能。但是这个过程是依赖于数据的,因此就需要用到专家知识,而且数据增广假设样本的领域共享同一个标签,并没有对不同类别的样本进行建模领域关系。
主要贡献
提供一种简单数据无关的数据增广方式,mixup,对训练数据集中数据任意两两线性插值:
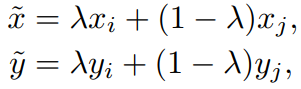
利用先验知识:对特征向量的线性插值会导致目标的线性插值,也就是说对y进行插值的合理性
mixup实现非常简单只需几行代码,但是只引入了非常小的计算负担
虽然极其简单,但是在CIFAR10/100, ImageNet2012上都取得了最好的结果,对于欺骗性的label或者对抗样本也更具有鲁棒性,在语音任务上和列表数据上提升了泛化性能,可以稳定GAN的训练过程
从ERM到mixup
expected risk:
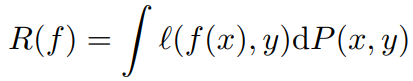
P(x,y)在实际场景中是不可知的,所以,我们用empirical distribution代替实际分布P(x,y)
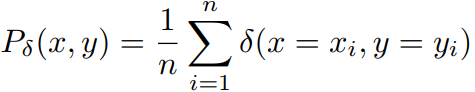
empirical risk:
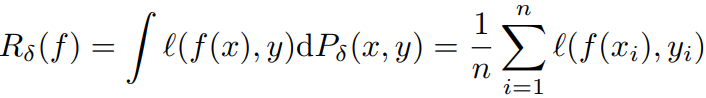
通过最小化上式来学习函数f就是Empirical Risk Minimization(ERM) 经验风险最小化
这个经验风险代表着有限的n的样本的行为,很容易就变成了强记忆训练数据。
根据VRM原理,经验分布可以由下式替换:
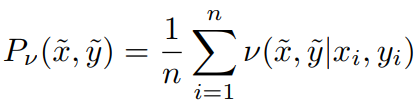
对于高斯近邻,可以认为就是在训练数据上增加了高斯噪声:
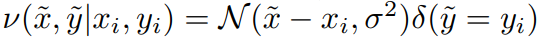
mixup的实现很简单直接,而且只引入了很小的计算负担。
What is mixup doing?
可以认为mixup vicinal distribution是一种数据增广方式使得模型f在训练数据上表现地线性,这种线性表现体现在当预测训练集外数据时会减少振荡。
Result