参考: http://blog.csdn.net/luo123n/article/details/48878759
Hinge Loss
也叫 max-margin objective 其最著名的应用是作为SVM的目标函数
其二分类情况下,公式如下:

y是预测值(-1与1之间,t是目标值+/-1)
其含义为,y的值在-1到1之间就可以了,并不鼓励|y|>1,即并不鼓励分类器过度自信,让某个可以正确分类的样本距离分割线的距离超过1并不会有任何奖励。从而使得分类器可以更专注整体的分类误差。
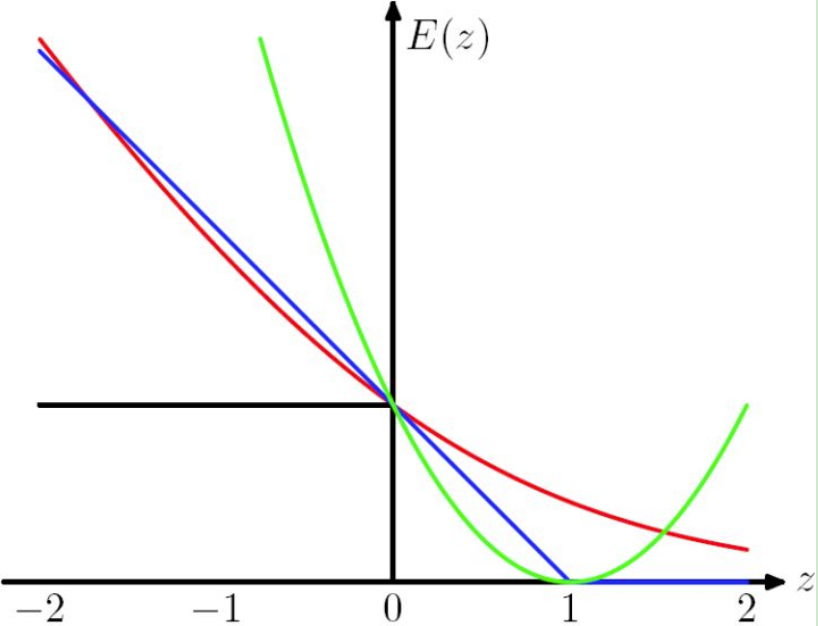
from PRML:
The Hinge Loss E(z) = max(0,1-z) is plotted in blue, the Log Loss in red, the Square Loss in green and the misclassification error in black.
换用其他的Loss函数的话,SVM就不再是SVM了。
知乎:正是因为HingeLoss的零区域对应的正是非支持向量的普通样本,从而所有的普通样本都不参与最终超平面的决定,这才是支持向量机最大的优势所在,对训练样本数目的依赖大大减少,而且提高了训练效率。
hinge loss是一个凸函数,很多常用的凸优化技术都可以使用。不过它是不可微的,只是有subgradient
参考: http://www.cnblogs.com/ooon/p/5539687.html
SVM求解使通过建立二次规划原始问题,引入拉格朗日乘子法,然后转换成对偶的形式去求解,这是一种理论非常充实的解法。这里换一种角度来思考,在机器学习领域,一般的做法是经验风险最小化 ERM ,即构建假设函数为输入输出间的映射,然后采用损失函数来衡量模型的优劣。求得使损失最小化的模型即为最优的假设函数,采用不同的损失函数也会得到不同的机器学习算法,比如这里的主题 SVM 采用的是 Hinge Loss ,Logistic Regression 采用的则是负 log 损失,
红色的线是log损失,E(x) = -log(P(Y|X))

对于二分类问题,假设分类器为y = wx+b, 根据经验风险最小化原则,这里引入二分类loss hinge loss:
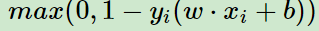
SVM可以通过直接最小化如下损失函数二求得最优的分离超平面:
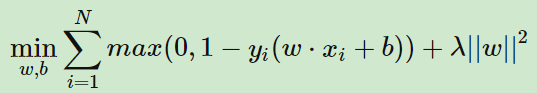
多分类问题:
单个样本多分类问题 s = wx+b s为向量,每个分量都是一个类的得分, y标签类别为1,其他为0
单个样本多分类的inge loss如下:

对每个分量进行hinge loss求和
所以k分类线性分类SVM的Hinge Loss表示为:

变种
实际应用中,我们的y值域并不是[-1,1],比如我们希望y更接近于一个概率,值域是[0,1], 另一方面,我们希望训练的是两个样本之间的相似关系,而非样本的整体分类,所以用以下公式:
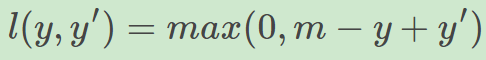
其中,y是正样本的得分,y'是负样本的得分,m是margin
我们并不希望正样本分数越高越好,负样本分数越低越好,但二者得分之差最多到m就足够了,差距增大并不会有任何奖励
比如,我们想训练词向量,我们希望经常同时出现的词,他们的向量内积越大越好;不经常同时出现的词,他们的向量内积越小越好。则我们的hinge loss function可以是:
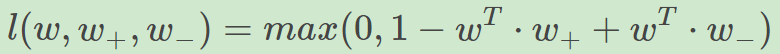
其中,w是当前正在处理的词,w+w+是w在文中前3个词和后3个词中的某一个词,w−w−是随机选的一个词
也就是说 1-正+负<=0 正-负>=1