一、有监督学习
1.概念:
目的在于从训练集中学习一个输入到输出的映射模型,再利用模型对未知数据进行预测。
由于训练集是人工给出的,所以叫有监督学习。
2.假设空间
假设空间指的是 输入到输出的所有映射模型的集合。机器学习的目的在于在假设空间中选取最优的模型。
3.模型分类
- 概率模型: 由条件概率分布函数
P(Y|X)表示 - 非概率模型: 由决策函数
Y=f(X)表示
4.问题定性
 ### 二、统计学习三要素
### 二、统计学习三要素
1.模型——输入与输出的映射
- 概率模型:条件概率分布
P(Y|X) - 非概率模型:决策函数
Y = f(X)
2.策略——模型好坏的评估标准
(1)损失函数(代价函数): 度量一次预测的好坏
表示预测值与实际值的偏差的函数,记为:L(Y, f(X))
常用的损失函数有:
- 0-1损失函数
- 平方损失函数
- 绝对损失函数
- 对数损失函数
(2) 期望风险(风险函数):理论上是模型 f(X) 关于联合分布 P(X ,Y) 的期望损失.
-
度量平均意义下预测的好坏。
-
由于期望风险不能直接计算,所以,可通过经验风险来近似。
(3) 经验风险:模型关于训练样本的平均损失
- 因此,当N-->无穷大,经验风险趋于期望风险,但是由于样本数量有限,容易用经验风险估计期望风险效果并不理想,因此所以需要对经验风险进行修正。
经验风险最小化和结构风险最小化
(1)经验风险最小化(ERM):
- 当样本容量够大,则经验风险最小化有较好的学习效果
- 模型为条件概率分布,损失函数为对数损失函数时,经验风险最小化就是 极大似然估计法
(2)结构风险最小化(SRM):
- 当样本容量太小,容易造成过拟合,因此结构风险在经验风险的基础上加了一个表示模型复杂度的正则化项(ragularizer)或罚项(penalty term)。
其中,J(f)为罚项,罚项越小,模型越复杂;罚项越大,模型越简单。$ lambda $是系数,用以权衡经验风险和模型复杂度。
因此结构风险最小化能够保证 经验风险 和 模型复杂度 都足够小。
此时监督学习问题就变成目标为 经验风险函数或结构风险函数最小化的优化问题
3.算法——求解最优模型的方法
- 即考虑用什么计算方法求解最优模型,即最优化算法。目前已有的最优化算法有很多,包括梯度下降,最小二乘法,牛顿法,也可以独自开发一些启发式算法。
4.模型选择
(1)过拟合
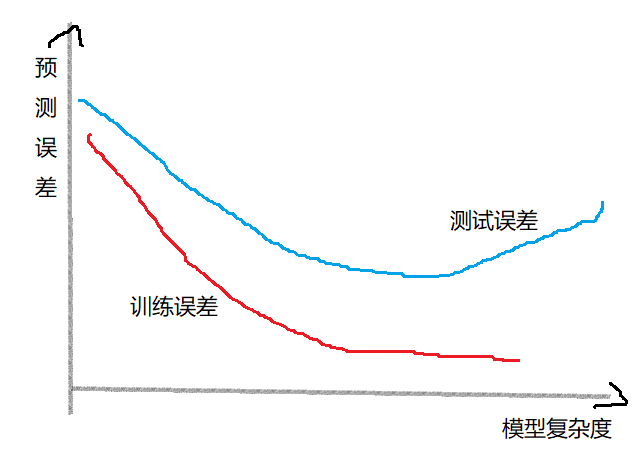
- 学习时选择的模型所包含的参数过多,以至于对已知数据预测很好,但对未知数据预测很差
训练误差与测试误差,和模型复杂度之间的关系
(2)模型选择方法
1.正则化——控制模型的复杂度
- 在经验风险上加一个正则化项,表示对模型复杂度的惩罚。正则化项一般是模型复杂度的递增函数,模型越复杂,正则化项越大。
- 奥卡姆剃刀原理(Occam's razor): 所有模型中,能很好的解释已知数据并且十分简单才是最好的模型。
2.交叉验证
1.简单交叉验证
- 简单把数据分成训练集和测试集,用训练集训练模型,用测试集评估模型。
2.S折交叉验证 - 将数据分成S个互不相交的子集,选择其中一个子集当测试集,剩下S-1个子集当训练集,重复S次。最后取S次结果的平均。
3.留一交叉验证 - 数据每次只留下一个样本用于当测试集,其他都是训练集。(一般在数据缺乏时使用)
5.生成模型和判别模型
(1)生成模型(generative model)
——由数据学习联合概率分布P(X,Y),求条件概率分布P(Y|X)作为预测的模型,模型给出了给给定输入X产生输出Y的生成关系。
典型的生成模型有:朴素贝叶斯、隐马尔科夫
特点:
- 可以还原出联合概率分布
- 收敛速度快
- 存在隐变量时,仍可用生成方法
(2)判别模型(discriminative model)
——由数据直接学习决策函数f(X)或者P(Y|X)作为预测的模型
典型的判别模型有:K邻近,感知机,决策树,逻辑回归,支持向量机,最大熵模型,提升方法,条件随机场等
特点:
- 学习准确率高
- 可以对数据进行各种程度上的抽象,定义特征并使用特征,以简化学习问题
6.分类问题
(1)评价指标
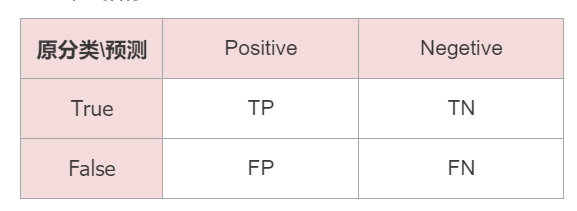
精确率(precision)
召回率(recall)
F1值——精确率和召回率的调和均值
为了更直观的理解这几个指标,可以看下图:
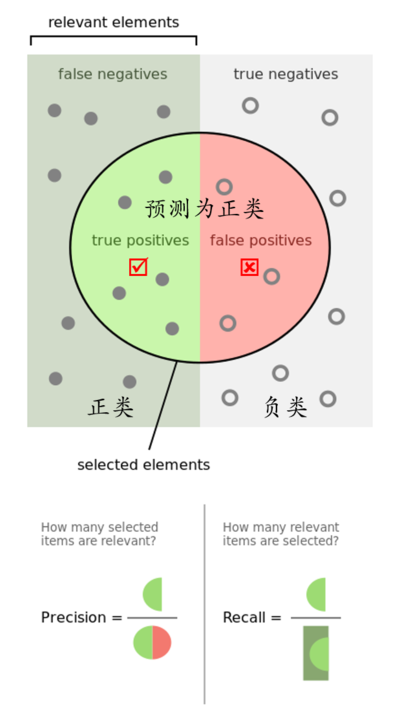
7.回归问题
——预测输入与输出的映射关系 (输入与输出都为连续值)
- 等价于函数拟合:选择一条曲线,使其很好的拟合已知数据,并且很好的预测未知数据
- 按输入变量个数,分为一元回归和多元回归
- 按输入输出变量之间的关系类型,分为线性回归和非线性回归
- 最常用的损失函数为平方损失函数,此时可用著名的 最小二乘法(least squares)求解。
8.标注问题
——预测输入与输出的映射关系 (输入与输出都为离散值)
- 典型模型有:隐马尔科夫模型、条件随机场