排序算法

#define LENGTH(array) ( (sizeof(array)) / (sizeof(array[0])) )
#define swap(a,b) do{a=a+b;b=a-b;a=a-b;}while(0) //两个数相同时 会导致结果为0

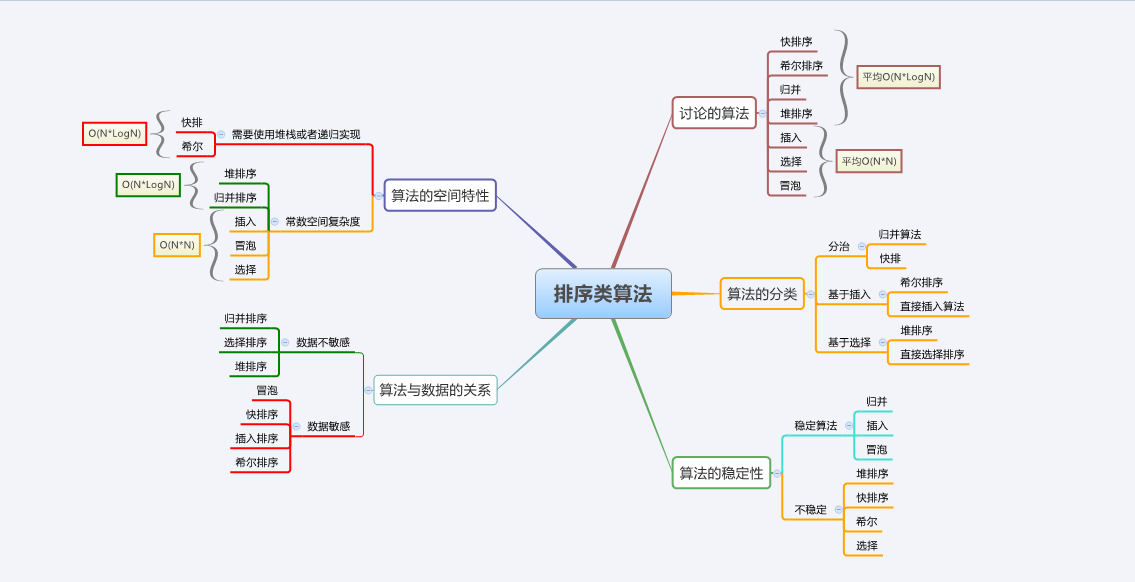
图片来源：https://blog.csdn.net/dyl_love98/article/details/8809000

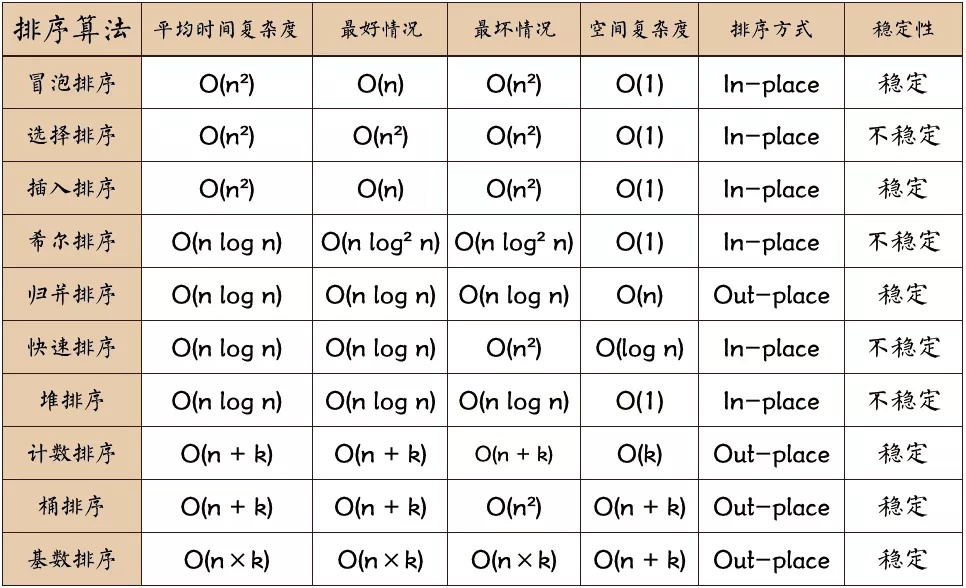
图片来源 https://www.zhihu.com/question/280279208/answer/829134919

一、插入排序

1、直接插入排序

/**
**  直接插入排序（插入到准确的位置）  不利于二分查找 直接遍历
**  时间复杂度：比较和移动和平均时间复杂度为O（n^2）  适合基本有序的序列，此时复杂度接近O（n）
**  空间复杂度：O(1)
**  稳定性：稳定
**/
void InsertSort(int a[], int n)
{
    int i, j;
    for (i = 2; i <=n; i++)//假设第一项已经排好，所以从第二项开始
    {
        if (a[i] < a[i - 1])//若此项小于 前面已经排好的最后一项（已排好的最大项）
        {
            a[0] = a[i];//0号位置为哨兵节点
            for (j = i - 1; a[0] < a[j]; j--)//从后 向前查找待插入位置
            {
                a[j+1] = a[j];//记录后移
            }
            a[j+1] = a[0];//复制到插入的位置 此时a[j]已经是小于a[0]的了
        }
    }
}

2、利用二分查找的直接插入排序

/**
**  插入排序（插入到准确的位置） 利用二分查找
**  比较复杂度：O（nlogn）
**  移动复杂度：O(n^2) 
**  时间复杂度为:O（n^2） 
**  稳定性：稳定
**/
void BInsertSort(int a[], int n)
{
    int i, j, low, high, mid;
    for (i = 2; i <= n; i++)
    {
        a[0] = a[i];//哨兵元素
        low = 1; high = i - 1;
        while (low <= high)
        {
            mid = (low + high) / 2;
            if (a[mid] > a[0])
                high = mid - 1;
            else
                low = mid + 1;
        }
        for (j = i - 1; j >=high+1; j--)
            a[j + 1] = a[j];
        a[high + 1] = a[0];
    }
}

3、希尔排序

/**
**  希尔排序 （缩小增量的排序）
**  最坏时间复杂度：O（n^2）
**  平均时间复杂度：O（n^1.3）
**  空间复杂度：O（1）
**  稳定性：不稳定 当相同关键字被划分到不同子表时 可能会造成不稳定
**/
void ShellSort(int a[], int n)
{
    //a[0] 是暂存单元 不是哨兵
    //进行插入排序的步长是dk 而不是1
    int i, j, dk;
    for (dk = n / 2; dk >= 1; dk = dk / 2)//步长变化
    {
        for (i = dk + 1; i <= n; i++)//对已经分好组的进行插入 排序 每一组都交替进行
        {
            if (a[i] < a[i - dk])//若当前项小于本组前一项
            {
                a[0] = a[i];//暂存在a[0]
                for (j = i - dk; j > 0 && a[0] < a[j]; j-=dk)//从本组已经排好序的序列中找到合适的插入位置
                    a[j + dk] = a[j];//记录后移
                a[j + dk] = a[0];//插入
            }
        }
    }
}

二、交换排序

1、冒泡排序

/**
**  冒泡排序（每次交换,将相邻中大的一个放在后面）
**  最坏时间复杂度：O（n^2）
**  平均时间复杂度：O（n^2）
**  最好情况下的复杂度：O(n) 初始序列有序时
**  空间复杂度：O（1）
**  稳定性：稳定
**/
//最大的上浮
void BubbleSort(int a[], int n)
{
    for (int i = 0; i < n - 1; i++)
    {
        int flag = 0;
        for (int j = 0; j < n - 1 - i; j++)//最大的向上浮
        {
            if (a[j] > a[j + 1])//此处若写等号 则变成不稳定的排序
            {
                swap(a[j], a[j + 1]);
                flag = 1;
            }
        }
        if (flag == 0) return;//一整趟都未交换一次 则已排序好 退出
    }
}

//最小的下浮
void BubbleSort_m(int a[], int n)
{
    for (int i = 0; i < n - 1; i++)
    {
        int flag = 0;
        for (int j = n-1; j >i; j--)//最小的向下浮
        {
            if (a[j-1] > a[j])//此处若写等号 则变成不稳定的排序
            {
                swap(a[j], a[j-1]);
                flag = 1;
            }
        }
        if (flag == 0) return;//一整趟都未交换一次 则已排序好 退出
    }
}

2、快速排序

/**
**  快速排序（任取枢轴pivot，将其分为小于pivot，和大于pivot的两部分，此时pivot放在了最终的位置上）
**  最坏空间复杂度O（n）
**  平均空间复杂度O（logn）
**  最坏时间复杂度：O（n^2）
**  平均时间复杂度：O（nlogn）
**  稳定性：不稳定 如若3为枢轴{3，2，2'} 经过一趟排序后 {2',2，3}
**/
int Partition(int a[], int low, int high)//根据枢轴划分两个区间
{
    int pivot = a[low];//将枢轴的值存起来
    while (low < high)
    {
        while (low < high && a[high] >= pivot) --high;//若高位有比枢轴小的 结束循环
        a[low] = a[high];//将高位比枢轴小的值放到低位上 
        while (low < high && a[low] <= pivot) ++low;//若低位有比枢轴大的值 结束循环 
        a[high] = a[low];//将低位比枢轴大的值放在高位上
    }
    a[low] = pivot;//将枢轴的值放到正确的位置上
    return low;//返回枢轴的位置
}
void QuickSort(int a[], int low, int high)
{
    if (low < high)
    {
        int pivotloc = Partition(a, low, high);
        QuickSort(a, low, pivotloc - 1);//依次对两个子表进行递归排序
        QuickSort(a, pivotloc + 1, high);
    }
}

三、选择排序

1、选择排序

/**
**  选择排序（每次选最小的）
**  空间复杂度O（1）
**  时间复杂度：O（n^2）
**  稳定性：不稳定 如若{2，2',1} 经过一趟排序后 {1,2',2}
**/
void SelectSort(int a[], int n)
{
    for (int i = 0; i < n - 1; i++)
    {
        int min = i;
        for (int j = i + 1; j < n; j++)
        {
                if (a[j] < a[min])
                    min = j;
        }
        if(min!=i)
            swap(a[i], a[min]);
    }
}

2、堆排序

/**
**  堆排序（每次选最小的）
**  空间复杂度O（1）
**  时间复杂度：O（nlogn） 建堆时间O（n） 向下平均调整时间O（nlogn）
**  稳定性：不稳定 如若{1,2，2'} 构造初始堆时将2交换到堆顶 {2,1,2'} 最终排序为{1,2',2}
**/

//将堆中小的节点调整至下方
void AdjustDown(int a[], int k, int len)
{
    a[0] = a[k];//用a[0]暂存根节点
    int i;
    for (i = 2 * k; i <= len; i *= 2)
    {
        if (i < len && a[i] < a[i + 1])//找出子数较大的一个
            i++;
        if (a[0] >= a[i])break;//如果根节点本来就大 无须调整
        else//叶子节点比较大
        {
            a[k] = a[i];//将较大的叶子节点调整到根节点
            k = i;//以原先未调整的较大的叶子节点的位置为根再进行调整 
        }
    }//for
    a[k] = a[0];//将最初暂存的根节点的值 放到最后一个做调整的叶子节点上去
}
//建大根堆
void BuildMaxHeap(int a[], int len)
{
    for (int i = len / 2; i > 0; i--)//从i=n/2到1 反复调整堆
        AdjustDown(a, i, len);
}
//堆排序
void HeapSort(int a[], int len)
{
    BuildMaxHeap(a, len);//建立大根堆
    show(a, 1,len, "after_build_max_heap:");
    for (int i = len; i > 1; --i)//将最后一个记录与大根堆的根节点对换
    {
        swap(a[1], a[i]);
        AdjustDown(a, 1, i - 1);//对根节点向下调整，序列长度为i-1 第i项为已经排列好的最大项
    }

}

四、归并排序

1、一个无序数组归并

/**
**  归并排序（分治法 每次分成左右两个子序列 且左右两个子序列有序）
**  空间复杂度O（n） 需要辅助数组b[]
**  时间复杂度：O（nlogn）
**  稳定性：稳定
**/
void Merge(int a[], int b[], int low, int mid, int high)
{
    //a是原数组 b是辅助数组 low-mid；mid+1-high 各自有序 将他们合并成一个有序表存放在a中
    int i, j, count;//count代表当前排序好的数据
    for (int k = low; k <= high; k++)//将a中所有的数据放到b中
        b[k] = a[k];
    for (i = low, j = mid + 1, count = low; i <= mid && j <= high; count++)//选择两个有序组中更小的一个放在a中
    {
        if (b[i] < b[j])
            a[count] = b[i++];
        else
            a[count] = b[j++];
    }
    //如下两个循环只会执行一个
    while (i <= mid) a[count++] = b[i++];//若第一个表未检测完 复制
    while (j <= high) a[count++] = b[j++];//若第二个表未检测完 复制
}
void MergeSort(int a[],int b[], int low, int high)
{
    if (low < high)
    {
        int mid = (low + high) / 2;//划分子序列
        MergeSort(a,b ,low, mid);//对左侧递归
        MergeSort(a,b, mid + 1, high);//右侧递归
        Merge(a, b, low, mid, high);//排序
        //show(b, 0, high+1, "b:");
    }
}

 2、两个有序数组归并

最差情况下：比较次数为 m+n-1

此时，将数组 arr1 与数组 arr2 中的元素两两比较，将值小的放进数组 arr3， 直到数组 arr3 填满为止。

因为 arr3 有 m+n 个空位，每次两两比较就放进去一个数，而最后一个剩下的元素可以不用比较直接放进去，所以一共两两比较了 m+n-1 次。

 

最好情况下：比较次数为 min{m, n}

有个疑问： 若一个数组为 1， 2，3 ； 另一个数组为 4, 5, 6, 7； 则直接将后一个数组最小的与前一个数组最大的比较，仅需一次比较就行了

一定要注意，这是简单归并排序，必须从第一个元素比。

因此，最好情况下，至少需要两两比较一个数组的长度，比较次数为 min{m,n}
————————————————
版权声明：本文为CSDN博主「心态与做事习惯决定人生高度」的原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接及本声明。
原文链接：https://blog.csdn.net/robert_chen1988/article/details/78718395

//双指针法 temp为辅助数组
class Solution {
public:
    void merge(vector<int>& nums1, int m, vector<int>& nums2, int n) {
        vector<int> temp(m);
        for(int i=0;i<m;i++)//将nums1的值复制到temp中
            temp[i]=nums1[i];
        nums1.clear();//clear之后size变为0 但容量不变
        int p=0,q=0;
        while(p<temp.size()&&q<nums2.size())
        {
            if(temp[p]<nums2[q])nums1.push_back(temp[p++]);//push_back 会使nums1的值++
            else nums1.push_back(nums2[q++]);
        }
        while(p<temp.size())
            nums1.push_back(temp[p++]);
        while(q<nums2.size())
            nums1.push_back(nums2[q++]);
        temp.swap(temp);//释放temp
    }
};

五、基数排序

/**
**  基数排序 基于关键字各位的大小进行排序
**  r代表基数 10进制时r=10
**  d代表最大数据的位数 
**  空间复杂度O（r）
**  时间复杂度：O（d（n+r）） 需要d趟分配和收集 一趟分配是O（n） 一趟收集是O(r)
**  稳定性：稳定
**  适用于k不是很大 序列较为集中 排序速度快于任何比较排序
**/
int maxbit(vector<int>& data) //辅助函数，求数据的最大位数
{
    int d = 1; //保存最大的位数
    int p = 10;
    int len = data.size();
    for (int i = 0; i < len; i++)
    {
        while (data[i] >= p)
        {
            p *= 10;
            ++d;
        }
    }
    return d;
}
void RadixSort(vector<int> &data) //基数排序
{
    int n = data.size();
    int r = 10;//基数r 此处为10
    vector<queue<int>> bucket(r);//r个队列 辅助存储空间
    int d = maxbit(data);
    int radix=1;//用来计算放在那个桶
    for (int k = 0; k < d; k++)//进行d趟分配和收集
    {
        //分配 
        for (int i = 0; i < n; i++)
            bucket[(data[i] / radix) % 10].push(data[i]);//(data[i] / radix) % 10指的是某数的某一位
        //收集
        int index = 0;//初始化数组大小
        for (int i = 0; i < r; i++)
        {
            while (!bucket[i].empty())
            {
                data[index++] = bucket[i].front();
                bucket[i].pop();
            }
        }
        radix *= 10;
    }
}