---恢复内容开始---
昨天,提交完我们的二叉树项目后,今天早上项目经理早早给我打电话;
他说,小伙子干的不错。但是为什么你上面的insert是recusive的呢?
你难道不知道万一数据量大啦!那得消耗很多内存哈!;
我大吃一惊,那么项目经理果然不是吃素的,他是在提醒我别投机取巧啦;
我们都知道递归实现树是比较简单的一种方式;
的确它的性能比较差,试想每次递归都要把当前函数压栈,然后出栈。。
好啦,那咱们今天就用非递归实现它;反正今天我就不干别的啦;
Problem
下面的代码你应该比较熟习啦!如果忘记啦请看C语言实现二叉树-01版
#include <stdio.h> #include <stdlib.h> typedef struct _node { int data; struct _node *link[2]; }Node; typedef struct _tree{ struct _node *root; }Tree; Tree * init_tree() { Tree *temp = (Tree*)malloc(sizeof(Tree)); temp->root = NULL; return temp; }
接下来我们重写insert的非递归实现:
int insert(Tree *tree, int data) { if(tree->root == NULL){ //TODO }else{ //TODO } return 1; }
我首先把框架写出来啦,就好比让你看看你将要完成的一座别墅建设的图纸;
要是你已经有“建设方案”啦!甚至可以暂时不要继续往下看,而是自己试着造出来;
当然,如果您还是没有什么头绪,那就烦劳您继续往下看看哦:)
显然,如果if语句tree->root == NULL成立,说明我们的树还未发芽呢。
何不给他来一朵嫩芽呢;
int insert(Tree *tree, int data) { if(tree->root == NULL){ tree->root = make_node(data); }else{ //TODO } return 1; }
好啦,现在不用考虑树的芽啦,现在要考虑的是else部分的树的生长问题啦;
为了在树的芽上继续生长,我们需要知道树根(注意其实这里得树芽指的是树根存在的确认)
我不知道怎么描述这些啦!如果我表达的不足以让你理解那就跳过这几行文字吧;
int insert(Tree *tree, int data) { if(tree->root == NULL){ tree->root = make_node(data); }else{ Node * it = tree->root; for(;;){ //TODO } } return 1; }
爬过树的朋友都知道,要想去摘果子,必须沿着树枝爬下去;
直到找到果子为止,因此,你需要一个遍历的过程;
而遍历通常是一个循环体;
现在你知道怎么构思下面的代码啦吗?
什么,还是不清楚哈?;
ok那么我们继续分析;
int insert(Tree *tree, int data) { if(tree->root == NULL){ tree->root = make_node(data); }else{ Node * it = tree->root; int dir; for(;;){ dir = it->data < data; if(it->data == data){ return 0; }else if(it->link[dir] == NULL){ break; } it = it->link[dir]; } //TODO } return 1; }
我们声明啦dir是direction(方向的意思);
它的值只有0,1这两种可能;
好啦看看一个小树;
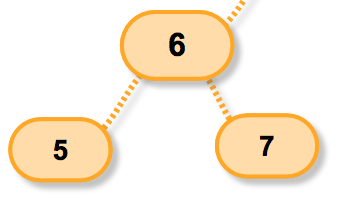
第一个if语句我们就不用进入啦!因为节点6 == NULL返回假,所以if部分不执行;
那么进入else部分;
假设我们要插入的数据是8,那么it-data < data用真正的数据展开呢就是
6<8显然,成立;
那么返回1,所以dir第一次代表的是1;
内层的if语句我们显然不会执行;
我们也不会执行else if部分;
好吧!我们执行一次it=it->link[dir];
刚才我们已经知道,dir代表的是1;
显然it现在指向啦它的右子树;(希望你还记得link[1]代表右子树,link[0]代表左子树);
此时,it已经指向啦节点7;
此时,你应该看看那个树是否有节点7;
好啦!我们继续循环;
又到啦
dir = it->data < data;
这行代码相当于:
if(it->data < data){ dir = 1; }else{ dir = 0; }
相信对你来说这是非常简单容易理解的;
那此时it所指的数据是7;
还记得我们要插入的数据是8吗?
显然7<8的,所以我们的dir还是1;
我们不会执行if语句的,这个原因请您思考吧;
我们直接走到啦else if语句;
if(it->data == data){ return 0; }else if(it->link[dir] == NULL){ break; }
我们发现,it->[dir]的确指向的是NULL;
好啦!我们找到啦!果子啦,我们应该break啦;
take break可能更加是人类需要的;
int insert(Tree *tree, int data) { if(tree->root == NULL){ tree->root = make_node(data); }else{ Node * it = tree->root; int dir ; for(;;){ dir = it->data < data; if(it->data == data){ return 0; }else if(it->link[dir] == NULL){ break; } it = it->link[dir]; } //TODO } return 1; }
( ⊙ o ⊙ )!怎么还有一个TODO啊!你会惊讶到我们不是已经找到啦目标啦吗;
的确,你找到啦,可是咱们没有把果子摘下来啊;
一起用力把果子摘下来吧(其实是把节点安装上去)
int insert(Tree *tree, int data) { if(tree->root == NULL){ tree->root = make_node(data); }else{ Node * it = tree->root; int dir ; for(;;){ dir = it->data < data; if(it->data == data){ return 0; }else if(it->link[dir] == NULL){ break; } it = it->link[dir]; } it->link[dir] = make_node(data); } return 1; }
it->link[dir]到底是指向哪啊?你不经会问;
再看看这图吧:

最后,你的8刚好插入到7得右子树下;
这就是你所有的工作啦;
#include <stdio.h> #include <stdlib.h> typedef struct _node { int data; struct _node *link[2]; }Node; typedef struct _tree{ struct _node *root; }Tree; Tree * init_tree() { Tree *temp = (Tree*)malloc(sizeof(Tree)); temp->root = NULL; return temp; } Node * make_node(int data) { Node *temp = (Node*)malloc(sizeof(Node)); temp->link[0] = temp->link[1] = NULL; temp->data = data; return temp; } int insert(Tree *tree, int data) { if(tree->root == NULL){ tree->root = make_node(data); }else{ Node * it = tree->root; int dir ; for(;;){ dir = it->data < data; if(it->data == data){ return 0; }else if(it->link[dir] == NULL){ break; } it = it->link[dir]; } it->link[dir] = make_node(data); } return 1; } void print_inorder_recursive(Node *root) { if(root){ print_inorder_recursive(root->link[0]); printf("data:%d ",root->data); print_inorder_recursive(root->link[1]); } return ; } void print_inorder(Tree *tree) { print_inorder_recursive(tree->root); return ; } int main(void) { Tree * tree = init_tree(); insert(tree,6); insert(tree,7); insert(tree,5); insert(tree,8); print_inorder(tree); return 0; }
运行结果如下;

好啦!非递归已经完成啦;
昨天的任务算是完成啦,今天的还没开始呢;
我们需要完成今天的新任务啦;
Problem
我们需要删除树上的某个节点,怎么办呢?
嘘,别先别想递归怎么实现啦,万一经理又不满意,明天还得改;
Solution
首先,我们需要理解几点;
第一,只有只是存在根的树才能被“砍”
int remove(Tree *tree, int data) { if(tree->root != NULL) { //TODO } return 1; }
所以代码大概是这样的结构;
而,要删除特定的节点,我们得先找到它;
因此,我们需要一个遍历的结构;
int remove(Tree *tree, int data) { if(tree->root != NULL) { Node *p = NULL; Node *succ; Node *it = tree->root; int dir; for(;;){ //TODO } } return 1; }
我们这里声明啦两个看起来比较陌生的面孔p 和succ;
p其实是parent(父亲)的缩写,succ是successor(继承者)的缩写;
先来看一看下面的树:
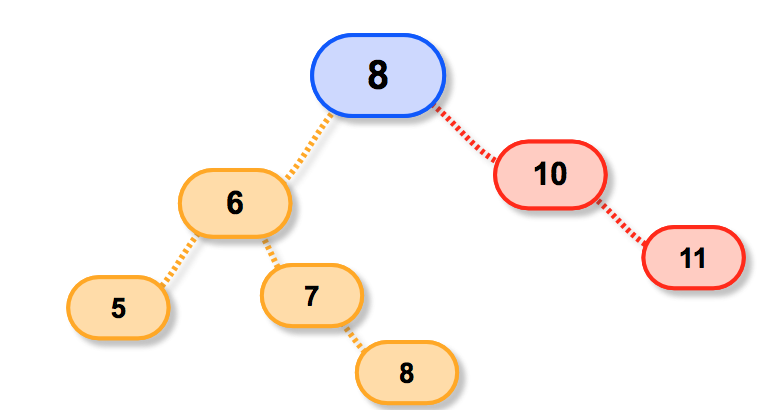
假设我们需要删除的节点是6;

继承者可能是7,就是他的大儿子哈(右子树);
可是呢!如果这棵树是这样的呢?
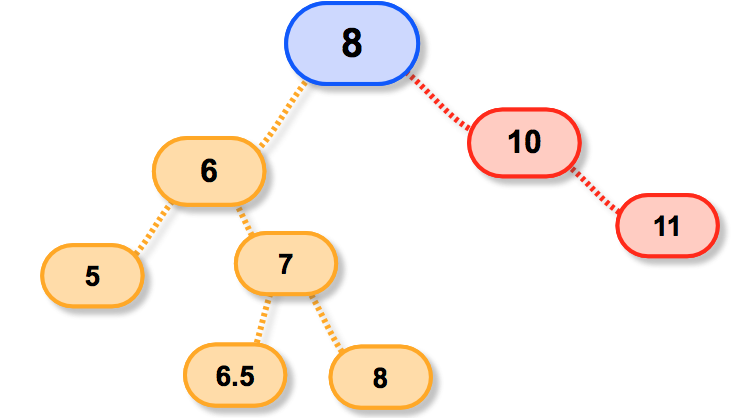
我们发现,假设再让7继承就会出现奇怪的现象;

这肯定不能叫做二叉树啦;
就好比,古代的皇帝,绝对不会有几个太子的;
因此,只有一个可以继承皇位,但是继承皇位的不一定是太上皇的儿子;
可能是其孙子;(好像古代就有这种情况出现,我历史学得差,不觉得啦)
所以正确的继承方式是:
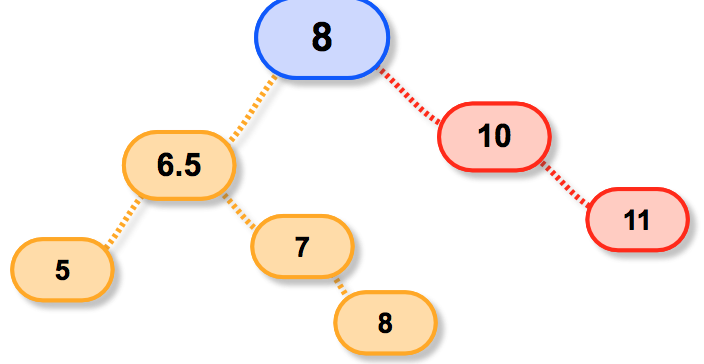
好啦!原理大概是这么啦,看看代码这么实现的吧:
int remove(Tree *tree, int data) { if(tree->root != NULL) { Node *p = NULL; Node *succ; Node *it = tree->root; int dir; for(;;){ if( it == NULL){ return 0; }else if(it->data == data){ break; } dir = it->data < data; p = it; it = it->link[dir]; } } return 1; }
你会发现,代码与插入的实现非常相似,只是多了一个 p = it;
这样坐的目的是,当it要深入到下一个分叉时,给自己留一个后路;
所以保存了自己的前一个备份;

看看这棵树,我们发现,当从7进入到8时;
p=it就是说p指向7;
而it可能是指向啦8;
当然也可能是指向啦5;
当找到我们的删除目标啦,我们就break;
退出for遍历,并且带着自己的老爸一起前进到下一关;
int remove(Tree *tree, int data) { if(tree->root != NULL) { Node *p = NULL; Node *succ; Node *it = tree->root; int dir; for(;;){ if( it == NULL){ return 0; }else if(it->data == data){ break; } dir = it->data < data; p = it; it = it->link[dir]; } /***********************************************************************/ if(it->link[0] != NULL && it->link[1] != NULL){ //TODO }else{ //TODO } } return 1; }
为啦,让我们的思路更加清晰,我们用*号分开上下部分;
第二关,看起来真是刺头,就if语句都那么长的条件;
那么它到底什么意思呢?
it->link[0] != NULL && it->link[1] != NULL
我们知道it是要删除的节点,那么它的link就是左右子树;
哦,好像意思有些明白啦;
就是说it都有孩子呗;

就好比是6.5一样,有两个儿子的情况;
如果这样的情况存在,那么6.5如果犯罪啦被执行死刑啦;
儿子是政府给养的;
所以if语句是这个意思哈;
if(it->link[0] != NULL && it->link[1] != NULL){ p = it; succ = it->link[1]; while(succ->link[0] != NULL){ p = succ; succ = succ->link[0]; } it->data = succ->data; p->link[p->link[1] == succ] = succ->link[1]; free(succ); }else{ //TODO }
为了,专注我们当前的问题,我们只这部分代码;
第一,p = it保留it的一份备份;
第二,succ = it->link[1]取it的右子树;
显然,有时候大儿子可以撑一个家的;
大儿子可能已经结婚啦,而且已经有啦儿子;
所以大儿子也希望找到自己最小得儿子(左子树)来管理家庭内务;
自己要外出干活;
所以
while(succ->link[0] != NULL){ p = succ; succ = succ->link[0]; }
往左找,一直找到最后一个,来再看一个图;

假设要删除的是6.5;
那么,首先找到7,就是succ=it->link[1];
但是发现,让7来管理家庭内务有些大才小用;
所以就是继续往左子树找succ=succ->link[0];
找到6.8后,while(succ->link[0] != NULL)不成立,退出;
找到啦继承者6.8;
而我们知道p总是走在succ的后面,所以succ不要的就留个p;
因此p此时指向的是6.9,比succ落后一点;
毕竟parent总是没有小朋友succ跑得快的;
it->data = succ->data;
我们注意到,要删除的it节点,没有如我们想象的delete (it->data)
而是直接让继承者的数据过来覆盖掉;
因此我们的图目前应该是这样的:

两个6.8节点显然是不对的啊;
所以想办法把6.8去掉才对;
p->link[p->link[1] == succ] = succ->link[1];
这行代码也是精致啊;
succ->link[1]可能存在,也可能只是NULL;
假设存在,应该我们的树可能是这样的;

显然,我们不能直接给原来的6.8设为NULL;
人家还有儿子呢;
所以让他得儿子也继承到6.8原来的父亲下面啦;
相当于,succ自己去当县长啦,让自己的父亲p照顾一下自己的儿子;

因此,我们的代码是这样写的;
p->link[p->link[1] == succ] = succ->link[1];
p->link[p->link[1] == succ]一般是等价于p->link[0]
因为,p->link[1] 通常不会等价于succ所以通常返回0;
因此,p->link[0]=succ->link[1]就是6.9接受6.85这个孙子的抚养权的过程;
那么什么时候,p->link[1] == succ成立呢?
p = it; succ = it->link[1];
注意看看,什么地方出现上面的代码;
你会发现,只有
while(succ->link[0] != NULL)
不执行,才会导致p->link[1]==succ成立;
也就才会返回1,也就才会让p->link[1]=succ->link[1]
看看图吧:

例如,假设删除的对象是5;
那么it指向5,而p也指向it,所以p也指向5;
succ=it->link[1]也就是说succ指向6;
继承者是6,发现while(succ->link[0] != NULL)不成立;
即,没有比6更小的啦;
可能是如下的树;

因此只能是6担当此次重任;

那么首先复制,6到5节点;
然后执行p->link[1]=succ->link[1];
好啦,说了那么多,休息一下下;
回顾一下我们这个函数完成的情况:
int remove(Tree *tree, int data) { if(tree->root != NULL) { Node *p = NULL; Node *succ; Node *it = tree->root; int dir; for(;;){ if( it == NULL){ return 0; }else if(it->data == data){ break; } dir = it->data < data; p = it; it = it->link[dir]; } /***********************************************************************/ if(it->link[0] != NULL && it->link[1] != NULL){ p = it; succ = it->link[1]; while(succ->link[0] != NULL){ p = succ; succ = succ->link[0]; } it->data = succ->data; p->link[p->link[1] == succ] = succ->link[1]; free(succ); /***********************************************************************/ }else{ //TODO } } return 1; }
不知不觉写了那么多代码啦;
可惜看到还有一个TODO你不经在想到底还有什么玩意,不能一次说清;
真是烦人,别急,再休息一会;
}else{ /*it->link[0] == NULL || it->link[1] == NULL */ dir = it->link[0] == NULL; if( p == NULL){ tree->root = it->link[dir]; }else{ p->link[p->link[1] == it] = it->link[dir]; } free(it); }
首先,判断it->link[0] == NULL;
然后判断p是否为NULL;
还记得这几行代码吗?
Node *p = NULL; Node *succ; Node *it = tree->root;
如果,p==NULL说明,it一直没有改变,因为p总是跟着it再改变的;
所以,此时,it任然是指向树根;
你可能大吃一斤;
不要惊讶,其意是说,我们找到啦你要删除的节点;
就是这棵树的根节点点,你确定要删除吗?
要是真的要,那么我们就给树换一个根啦;
tree->root = it->link[dir];
还要注意一个问题,要换这棵树的根的前提是;
这棵树只有一个儿子,
可能是左儿子,也可能是右儿子;
只有右儿子的情况:

只有左儿子的情况:

无论怎样,这个儿子都是直接继承啦!没人跟他争啦;
好啦再看看这个if-else语句到底还包含什么:
if( p == NULL){ tree->root = it->link[dir]; }else{ p->link[p->link[1] == it] = it->link[dir]; }
如果p!=NULL呢?
那就是说,我们处理的节点肯定含有叶子的节点;
首先分析,it->link[dir]表示我们要删除的节点到底还有哪个儿子;
dir = it->link[0] == NULL;
还记得上面这行代码吗?如果我们的左边为空那么返回右边的儿子;
因此,你可以简单的理解dir代表着it还有的唯一一个儿子所在的位置;
这个儿子必须继承下来;
而到底继承到谁家你呢;
看it得父亲要怎么收养啦;
要是p就是树根;
it就是根的右子树;
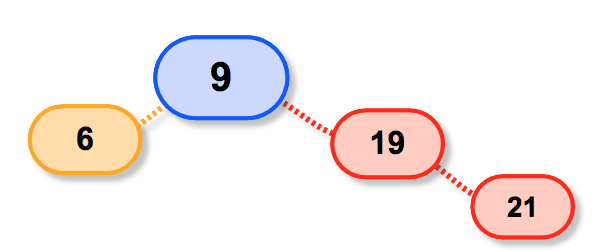
显然,满足p->link[1]==it所以返回1
此时p->link[1]=it->link[dir];
即,19被删除啦,然后是21接上;
第二种情况,如果p->link[1]!=it呢;

这种情况是,p是19,那么it就是17要删除的节点;
p->link[1]!=17而是等于21所以返回0
因此p->link[0]=it->link[dir];
哈哈,这正是我们想要的效果;

好啦!任务总算是完成啦;
看看我们的整体成果吧;
int remove(Tree *tree, int data) { if(tree->root != NULL) { Node *p = NULL; Node *succ; Node *it = tree->root; int dir; for(;;){ if( it == NULL){ return 0; }else if(it->data == data){ break; } dir = it->data < data; p = it; it = it->link[dir]; } /***********************************************************************/ if(it->link[0] != NULL && it->link[1] != NULL){ p = it; succ = it->link[1]; while(succ->link[0] != NULL){ p = succ; succ = succ->link[0]; } it->data = succ->data; p->link[p->link[1] == succ] = succ->link[1]; free(succ); /***********************************************************************/ }else{ /*it->link[0] == NULL || it->link[1] == NULL */ dir = it->link[0] == NULL; if( p == NULL){ tree->root = it->link[dir]; }else{ p->link[p->link[1] == it] = it->link[dir]; } free(it); } } return 1; }
编译有错:

搞啦半天,原来已经有已经函数叫做remove啦
好吧咱们换个名字;
#include <stdio.h> #include <stdlib.h> typedef struct _node { int data; struct _node *link[2]; }Node; typedef struct _tree{ struct _node *root; }Tree; Tree * init_tree() { Tree *temp = (Tree*)malloc(sizeof(Tree)); temp->root = NULL; return temp; } Node * make_node(int data) { Node *temp = (Node*)malloc(sizeof(Node)); temp->link[0] = temp->link[1] = NULL; temp->data = data; return temp; } int insert(Tree *tree, int data) { if(tree->root == NULL){ tree->root = make_node(data); }else{ Node * it = tree->root; int dir ; for(;;){ dir = it->data < data; if(it->data == data){ return 0; }else if(it->link[dir] == NULL){ break; } it = it->link[dir]; } it->link[dir] = make_node(data); } return 1; } void print_inorder_recursive(Node *root) { if(root){ print_inorder_recursive(root->link[0]); printf("data:%d ",root->data); print_inorder_recursive(root->link[1]); } return ; } void print_inorder(Tree *tree) { print_inorder_recursive(tree->root); return ; } int remove_node(Tree *tree, int data) { if(tree->root != NULL) { Node *p = NULL; Node *succ; Node *it = tree->root; int dir; for(;;){ if( it == NULL){ return 0; }else if(it->data == data){ break; } dir = it->data < data; p = it; it = it->link[dir]; } /***********************************************************************/ if(it->link[0] != NULL && it->link[1] != NULL){ p = it; succ = it->link[1]; while(succ->link[0] != NULL){ p = succ; succ = succ->link[0]; } it->data = succ->data; p->link[p->link[1] == succ] = succ->link[1]; free(succ); /***********************************************************************/ }else{ /*it->link[0] == NULL || it->link[1] == NULL */ dir = it->link[0] == NULL; if( p == NULL){ tree->root = it->link[dir]; }else{ p->link[p->link[1] == it] = it->link[dir]; } free(it); } } return 1; } int main(void) { Tree * tree = init_tree(); insert(tree,6); insert(tree,7); insert(tree,5); insert(tree,8); print_inorder(tree); puts("remove 6"); remove_node(tree,6); print_inorder(tree); insert(tree,12); print_inorder(tree); puts("remove 5"); remove_node(tree,5); print_inorder(tree); return 0; }
最后运行结果如下:
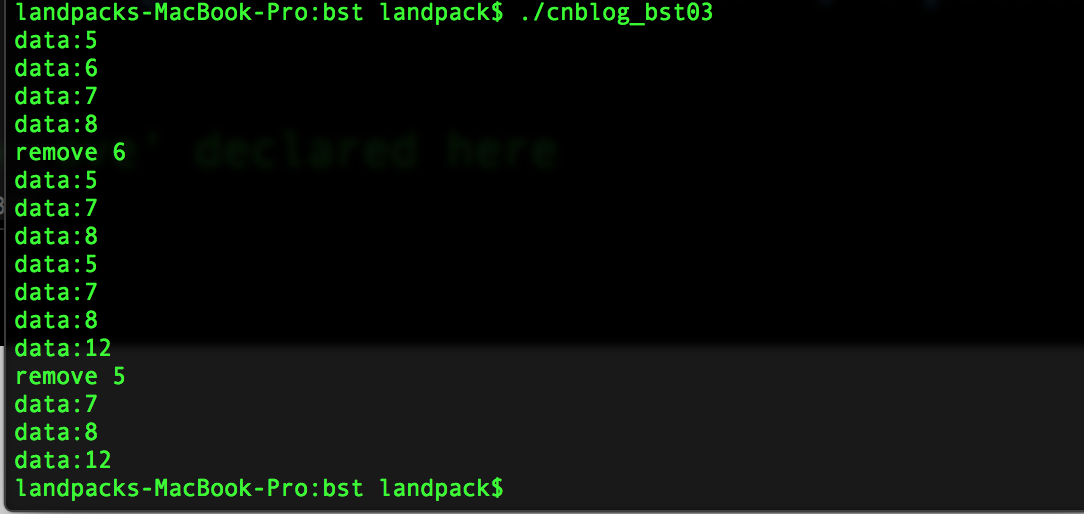
Thanks:)