最短路径求解(Dijkstra)

Dijkstra算法分析

题目分析参照《数据结构》(严蔚敏)7-6节

最短路径问题描述

参照日常生活中的公交查询系统。我们有选项：

少换乘/最少站数

价格最少/时间最短....

（ps:下边这个图是网页查询的，略有出入）

根据这样的分类。我们可以将最短路径分为：结点最少(经过的站数最少)，权值最小（这个就是个心里期望了，看你是相花费时间最少，金钱最少....）

结点最少

（参照途中描述）

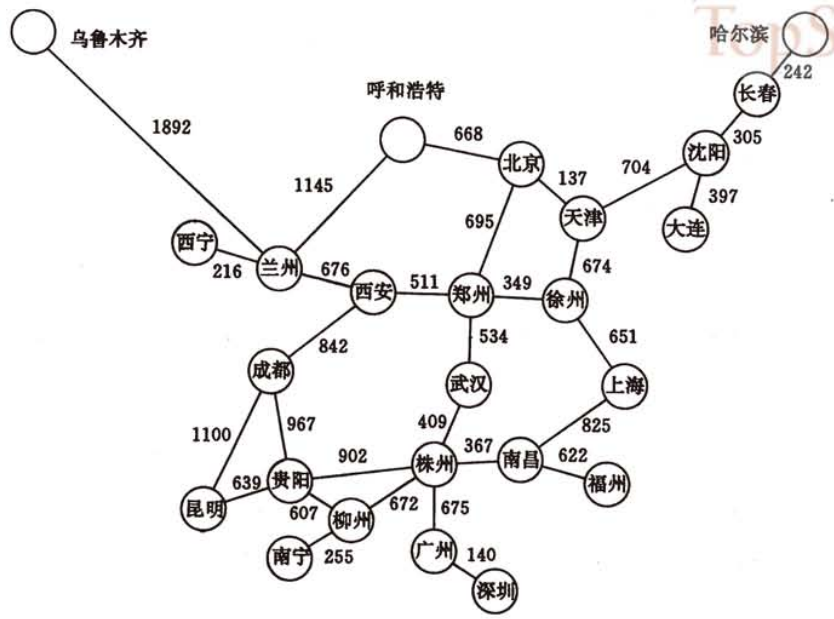
由此可以看出，对于经过站点最少，换乘最少这种问题，我们只需要对图进行广度遍历，即可获取相关结果。

我们重点分析下面的情况

权值最小（花费最少）

理论：从A到B，他们之间的路径要么是A->B,要么经过中间节点  A->..->B其最短路径也就是两条路径中最短的一条。

于是有：对于最短路径问题，我们只需要利用动态规划，在遍历中更新，逐步获取最短路径。

具体分析图如下

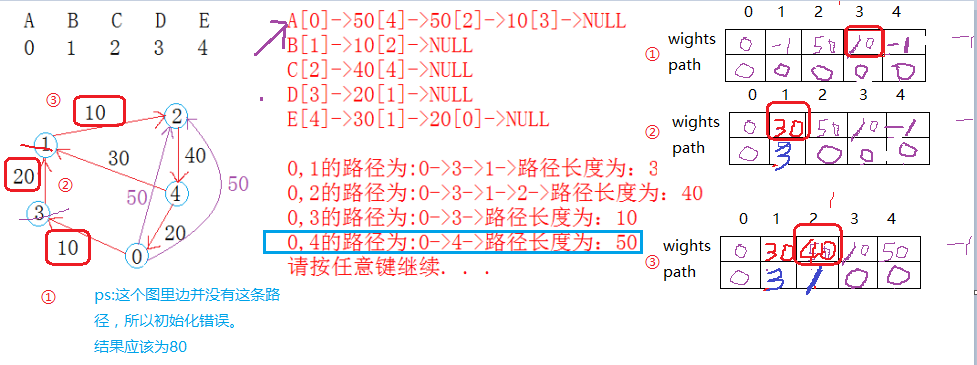
如上为寻找下标0-2结点过程的分析。对应代码

    bool Dijkstra(const V&src,const V&dst,int &ret)
    {
        //如果只有顶点，那么返回true，ret =0；
        if (_size <= 1)
        {
            ret = 0;
            return true;
        }
        int cur = FindIndexV(src);
        int end = FindIndexV(dst);
        
        int beg = cur;

        size_t wights[6] = {};
        int paths[6] = {};
        for (size_t i = 0; i < _size; ++i)
        {
            wights[i] = -1;
            paths[i] = src;
        }
        wights[cur] = 0;
        paths[cur] = 0;

        Edge* pcur = _eList[cur];
        //首次更新
        while (pcur)
        {
            wights[pcur->_dst] = pcur->_wight;
            pcur = pcur->_next;
        }
        pcur = _eList[cur];

        int visitedCount = 0;
        while (cur!=end)//未走到目的
        {
            if (cur == beg)
                visitedCount++;
            //如果起点没有路径且目标不可达//或者回到起点了
            if (pcur == NULL&&wights[dst] == -1||cur == beg&&visitedCount==2)
            {
                return false;
            }

            //获取最短边
            Edge* minCur = _eList[cur];
            Edge* pcur = _eList[cur];
            while (pcur)    
            {
                if (minCur->_wight > pcur->_wight)
                    minCur = pcur;
                pcur = pcur->_next;
            }
            cur = minCur->_src;
            //根据局部最短更新路径
            if (wights[cur] + minCur->_wight < wights[minCur->_dst])
            {
                wights[minCur->_dst] = wights[cur] + minCur->_wight;
                paths[minCur->_dst] = minCur->_src;
            }

            cur = minCur->_dst;
            if (minCur->_dst == FindIndexV(dst))
            {
                ret = wights[minCur->_dst];
                return true;
            }
        }
    }

以下是整个图项目文件以及对应于最短路径的测试用例

#pragma once
//邻接表实现图

#include<queue>
#include<stack>
#include"UnionFindset.h"

#include<map>
template<class V, class E>
struct Edge
{
    Edge(size_t dst,size_t src, const E&e)
        :_wight(e)
        ,_dst(dst)
        ,_src(src)
        , _next(NULL)
    {}
    E _wight;       //权值，边比重
    size_t _dst;    //目的顶点下标
    size_t _src;    //源顶点下标
    struct Edge<V, E>* _next;

    bool operator<(const Edge* &ed)
    {
        return _wight < ed->_wight;
    }
};

template<class V,class E>
class GraphList
{
    typedef Edge<V, E> Edge;
protected:
    V* _vArr;               //顶点存储数组 
    size_t _size;
     
    Edge** _eList;    //边存储指针数组

public:
    GraphList(const V* vArray, const size_t size)
        :_size(size)
        , _vArr(new V[size])
    {
        //初始化顶点保存
        for (size_t i = 0; i < size; ++i)
        {
            _vArr[i] = vArray[i];
        }
        //初始化边结构
        _eList = new Edge*[size];
        memset(_eList, 0, sizeof(Edge*)*size);
    }

    int FindIndexV(const V& v) const
    {
        for (size_t i = 0; i < _size; ++i)
        {
            if (_vArr[i] == v)
                return i;
        }
        return -1;
    }

    //添加v1->v2的边
    void AddEdge2(const V& v1, const V&v2, const E& e, bool IsDir = true)
    {
        int ind1 = FindIndexV(v1);
        int ind2 = FindIndexV(v2);

        Edge* cur = new Edge(ind2, ind1, e);

        cur->_next = _eList[ind1];
        _eList[ind1] = cur;

        if (!IsDir)
        {
            Edge* cur = new Edge(ind1, ind2, e);
            cur->_next = _eList[ind2];
            _eList[ind2] = cur;
        }

    }


    void Display()const
    {
        cout << "顶点集合" << endl;
        for (size_t i = 0; i < _size; ++i)
        {
            cout << _vArr[i] << " ";
        }
        cout << endl << "边表示" << endl;


        for (size_t i = 0; i < _size; ++i)
        {
            cout << "边["<<i << "]>>";
            Edge* cur = _eList[i];
            while (cur)
            {
                //cout << "[" << cur->_dst << "]" << cur->_wight << " ";
                //printf("[%d]:", cur->_dst, cur->_wight);
                cout << "[" << cur->_dst << "]" << cur->_wight << "--> ";
                cur = cur->_next;
            }
            cout <<"NULL"<< endl;
        }
        cout << endl;
    }

    //广度优先
    void BSP(const V& root)
    {
        cout << "广度优先遍历：" << endl;
        bool *visited = new bool[_size]();

        queue<int> q;
        int index = FindIndexV(root);

        q.push(index);

        while (!q.empty())
        {
            index = q.front();
            if (visited[index] == false)
            {
                cout << _vArr[index]<<"-->";
            }

            visited[index] = true;

            q.pop();
            Edge* cur = _eList[index];
            while (cur)
            {
                if (visited[cur->_dst] == false)//未访问过那么压入
                {
                    q.push(cur->_dst);
                }
                cur = cur->_next;
            }
        }
        cout << endl << endl;
    }

    //深度优先
    void DSP(const V& root)
    {
        //
        cout << "深度优先遍历：" << endl;
        _DSP(root);
        cout << endl << endl;
    }
    void _DSP(const V& root)
    {
        static bool *visited = new bool[_size]();
        int index = FindIndexV(root);
        if (visited[index] == false)
        {
            cout << _vArr[index] << "-->";
            visited[index] = true;
        }
        
        Edge* cur = _eList[index];

        while (cur)
        {
            if (visited[cur->_dst] == false)
                _DSP(_vArr[cur->_dst]);
            cur = cur->_next;
        }
        if (cur == NULL)
            return;
    }

    //在所有边中获取最小权值的边
    int FindMinEdgeIndex(vector<Edge*>&v)
    {
        int min = 0;
        for (size_t i = 1; i < v.size(); ++i)
        {
            if (v[i]->_wight < v[min]->_wight)
                min = i;
        }
        return min;
    }

    bool Kruskal(GraphList<V,E>& minTree)
    {
        vector<Edge*> ve;
        for (size_t i = 0; i < _size; ++i)
        {
            Edge* cur = _eList[i];
            while (cur)
            {
                //只插入有效边
                ve.push_back(cur);
                cur = cur->_next;
            }
        }

        UnionFindSet us(_size);

        while (!ve.empty())
        {
            //找到最小权值边
            int i = FindMinEdgeIndex(ve);
            //并查集插入相关结点
            bool sure = us.Combine(ve[i]->_src, ve[i]->_dst);
            if (sure)   //如果不是连通的，那么加入该边
            {
                minTree.AddEdge2(_vArr[ve[i]->_src], _vArr[ve[i]->_dst], ve[i]->_wight);
            }
            ve.erase(ve.begin()+i);
        }

        return us.IsOnlyOneRoot();
    }


    //在相关边中获取最小权值的边
    int FindMinEdgeIndexByInGraph(vector<Edge*>&v,vector<int>& nodes)
    {
        if (nodes.size() == 0)
            return FindMinEdgeIndex(v);
        int min = -1;
        for (size_t i = 0; i < v.size(); ++i)   //遍历所有结点
        {
            //如果
      
            if (v[i]->_wight < v[min]->_wight)
            {
                bool inNodes = false;
                for (size_t j = 0; j < nodes.size(); ++i)
                {
                    if (v[i]->_dst == nodes[j] || v[i]->_src == nodes[j])
                    {
                        inNodes = true;
                        break;
                    }
                } 
                if(inNodes)
                    min = i;
            }      

        }
        return min;
    }
    bool Prim(GraphList<V, E>& minTree)
    {
        vector<Edge*> ve;
        vector<int> inGraph;
        for (size_t i = 0; i < _size; ++i)
        {
            Edge* cur = _eList[i];
            while (cur)
            {
                //只插入有效边
                ve.push_back(cur);
                cur = cur->_next;
            }
        }

        UnionFindSet us(_size);

        while (!ve.empty())
        {
            //找到最小权值边
            int i = FindMinEdgeIndexByInGraph(ve,inGraph);
            if (us.IsOnlyOneRoot())
                return true;

            else if (i == -1 && !us.IsOnlyOneRoot())
                return false;
            
            //并查集插入相关结点
            bool sure = us.Combine(ve[i]->_src, ve[i]->_dst);
            if (sure)   //如果不是连通的，那么加入该边
            {
                minTree.AddEdge2(_vArr[ve[i]->_src], _vArr[ve[i]->_dst], ve[i]->_wight);
            }
            ve.erase(ve.begin() + i);
        }

        return us.IsOnlyOneRoot();
    }
    //size_t wights[6] = {};
    //int paths[6] = {};
    bool Dijkstra(const V&src,const V&dst,int &ret)
    {
        //如果只有顶点，那么返回true，ret =0；
        if (_size <= 1)
        {
            ret = 0;
            return true;
        }
        int cur = FindIndexV(src);
        int end = FindIndexV(dst);
        
        int beg = cur;

        size_t wights[6] = {};
        int paths[6] = {};
        for (size_t i = 0; i < _size; ++i)
        {
            wights[i] = -1;
            paths[i] = src;
        }
        wights[cur] = 0;
        paths[cur] = 0;

        Edge* pcur = _eList[cur];
        //首次更新
        while (pcur)
        {
            wights[pcur->_dst] = pcur->_wight;
            pcur = pcur->_next;
        }
        pcur = _eList[cur];

        int visitedCount = 0;
        while (cur!=end)//未走到目的
        {
            if (cur == beg)
                visitedCount++;
            //如果起点没有路径且目标不可达//或者回到起点了
            if (pcur == NULL&&wights[dst] == -1||cur == beg&&visitedCount==2)
            {
                return false;
            }

            //获取最短边
            Edge* minCur = _eList[cur];
            Edge* pcur = _eList[cur];
            while (pcur)    
            {
                if (minCur->_wight > pcur->_wight)
                    minCur = pcur;
                pcur = pcur->_next;
            }
            cur = minCur->_src;
            //根据局部最短更新路径
            if (wights[cur] + minCur->_wight < wights[minCur->_dst])
            {
                wights[minCur->_dst] = wights[cur] + minCur->_wight;
                paths[minCur->_dst] = minCur->_src;
            }

            cur = minCur->_dst;
            if (minCur->_dst == FindIndexV(dst))
            {
                ret = wights[minCur->_dst];
                return true;
            }
        }
    }

    ~GraphList()
    {
        if (_vArr)
        {
            delete[]_vArr;
            _vArr = NULL;
        }
        if (_eList)
        {
            for (size_t i = 0; i < _size;++i)
            {
                while (_eList[i] != NULL)
                {
                    Edge* del = _eList[i];
                    _eList[i] = del->_next;
                    delete del;
                    del = NULL;
                }
            }
        }
    }
};



void testD()
{
    //int vArr1[] = { 1,2,3,4,5,6,7,8,9 };
    //GraphList<int, int> gh1(vArr1, sizeof(vArr1) / sizeof(vArr1[0]));

    //gh1.AddEdge2(1, 2, 11);
    //gh1.AddEdge2(1, 3, 33);
    //gh1.AddEdge2(1, 5, 33);
    //gh1.AddEdge2(2, 3, 33);
    //gh1.AddEdge2(2, 6, 99);
    //gh1.AddEdge2(5, 3, 33);
    //gh1.AddEdge2(3, 4, 44);
    //gh1.AddEdge2(4, 5, 55);
    //gh1.AddEdge2(4, 7, 32);
    //gh1.AddEdge2(7, 8, 65);
    //gh1.AddEdge2(1, 9, 12);
    //gh1.AddEdge2(9, 7, 22);    

    int vArr1[] = { 0,1,2,3,4,5};
    GraphList<int, int> gh1(vArr1, sizeof(vArr1) / sizeof(vArr1[0]));

    gh1.AddEdge2(0, 3, 10);
    gh1.AddEdge2(0, 2, 50);
    gh1.AddEdge2(3, 1, 20);
    gh1.AddEdge2(1, 2, 10);
    gh1.AddEdge2(2, 4, 40);
    gh1.AddEdge2(4, 0, 20);
    gh1.AddEdge2(4, 1, 30);
    gh1.AddEdge2(5, 1, 10);



    gh1.Display();

    gh1.BSP(1);
    gh1.DSP(1);
    GraphList<int, int> gMin(vArr1, sizeof(vArr1) / sizeof(vArr1[0]));
    GraphList<int, int> gMin1(vArr1, sizeof(vArr1) / sizeof(vArr1[0]));
    if (gh1.Kruskal(gMin))
    {
        cout << "kruskal最小生成树：" << endl;
        gMin.Display();
    }
    if (gh1.Prim(gMin1))
    {
        cout << "prim最小生成树：" << endl;
        gMin1.Display();
    }

    int ret = 0;
    if (gh1.Dijkstra(0, 1, ret))
    {
        cout <<"gh1.Dijkstra(0, 1, ret)"<< ret << endl;
    }
    if (gh1.Dijkstra(0, 2, ret))
    {
        cout << "gh1.Dijkstra(0, 2, ret)" << ret << endl;
    }
    if (gh1.Dijkstra(0, 3, ret))
    {
        cout << "gh1.Dijkstra(0, 3, ret)" << ret << endl;
    }
    if (gh1.Dijkstra(0, 4, ret))
    {
        cout << "gh1.Dijkstra(0, 4, ret)" << ret << endl;
    }
    if (gh1.Dijkstra(0, 5, ret))
    {
        cout << "gh1.Dijkstra(0, 5, ret)" << ret << endl;
    }
    //char vArr2[] = { 'A','B','C','D','E','F' };
    //GraphList<char, int> gh(vArr2, sizeof(vArr2) / sizeof(vArr2[0]));
    //gh.AddEdge2('A', 'B', 11);
    //gh.AddEdge2('B', 'C', 33);
    //gh.AddEdge2('C', 'D', 44);
    //gh.AddEdge2('D', 'E', 55);
    //gh.AddEdge2('E','F', 66);
    //gh.Display();

 //   gh.BSP('A');
}

参考:http://www.cnblogs.com/hxsyl/archive/2013/08/20/3270401.html