一、仿照三元组或复数的抽象数据类型写出有理数抽象数据类型的描述 (有理数是其分子、分母均为整数且分母不为零的分数)。有理数基本运算:
1、构造有理数T,元素e1,e2分别被赋以分子、分母值
2、销毁有理数T
3、用e(引用类型参数)返回有理数T的分子或分母,当入参i为1时返回分子, i为2是返回分母。
4、将有理数T的分子或分母更改为e,入参i为1时改变分子, i为2是改变分母
5、有理数T1,T2相加,结果存入有理数T3
6、有理数T1,T2相减,结果存入有理数T3
7、有理数T1,T2相乘,结果存入有理数T3
8、有理数T1,T2相除,结果存入有理数T3
ADT RationalNumber{
数据对象:D = {e1,e2|e1,e2都属于ElemType类型}
数据关系:R = {<e1,e2>}
基本操作:
InitRationalNumber(&T,e1,e2)
操作结果:构造一个有理数T,其分子和分母分别为e1和e2
DestoryRationalNumber(&T)
操作结果:销毁有理数T
Get(T,i,&e)
操作结果:用e返回有理数T的分子或分母,i为1时返回分子, i为2是返回分母
Put(&T,i,e)
操作结果:将有理数T的分子或分母更改为e,i为1时改变分子, i为2是改变分母
AddRationalNumber(T1,T2,&T3)
操作结果:将T1,T2相加,结果存入T3
SubtractionRationalNumber(T1,T2,&T3)
操作结果:将T1,T2相减,结果存入T3
MultiplicationRationalNumber(T1,T2,&T3)
操作结果:将T1,T2相乘,结果存入T3
DivisionRationalNumber(T1,T2,&T3)
操作结果:将T1,T2相除,结果存入T3
} ADT RationalNumber
二、实验
1、数据结构、函数说明

2、代码实现说明
e1,e2是T1的分子分母;e3,e4是T2的分子分母 ;e5,e6是T3的分子分母
(1)相加

(2)相减

(3)相乘

(4)相除

(5)计算公约数:实现方法:辗转相除法

3、结果展示
(1)测试1:T1>T2
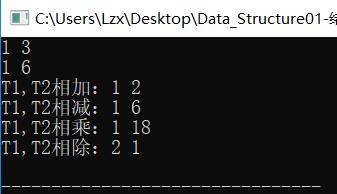
(2)测试2:T1<T2
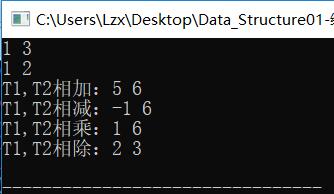
(3)测试3:T1=T2
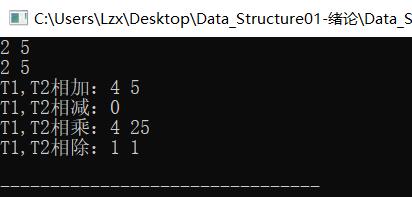
(4)测试4:异常数据

4、总结
1. “数据结构”定义为一个二元组(D,S),即两个集合,D是数据元素的集合,S是数据元素之间一个或多个关系的集合。
2. “抽象数据类型”本质是“数据类型”,与计算机相关,涉及数据的存储及如何用存储来反应数据元素之间的关系。它定义为一个三元组(D,S,P),加上的P是定义的一组针对存储的数据操作(如插入,删除,排序等)。
3. 抽象数据类型是一个数学模型以及定义在该模型上的一组操作,抽象数据类型的定义仅取决与它的一组逻辑特性,而与其在计算机内部如何表示和实现无关,即不论其内部结构如何变化,只要它的数字特性不变,都不影响其外部的使用。
三、使用git命令行上传代码到码云