源地址:http://www.cnblogs.com/drizzlecrj/archive/2008/02/25/1077494.html
1)将256*256分辨率的图像变为128*128分辨率可以将源图像划分成2*2的子图像块,然后将2*2的
子图像块的所有像素颜色均按照F(i,j)的颜色值进行设定,达到降低分辨率的目的。
如:
F(i,j) F(i,j+1) F(i,j) F(i,j)
F(i+1,j) F(i+1,j+1) 变成 F(i,j) F(i,j)
(同理,256*256分辨率的图像变成64*64分辨率,只需要划分成4*4即可,以此类推。)
2) R单色, G单色,B单色化图像,只需要将图像的每一个像素中的相应的R, G, B值取出,然后利用类似
(R,R,R),(G,G,G),(B,B,B)的像素重新绘制即可。
3) 彩色图像的RGB和亮度Y,色差I,信号值Q的关系
| Y | |0.31 0.59 0.11 | | R |
| I | = |0.60 -0.28 -0.32 | * | G |
|Q | |0.21 -0.52 -0.31 | | B |
即 Y = 0.31R + 0.59G+0.11B
I = 0.60R - 0.28G - 0.32B
Q = 0.21R - 0.52B - 0.31B
4) 彩色图像的逆反处理: 将对应的(R, G, B)像素替换成(255 - R, 255 - G, 255 - B)
彩色图像的平滑处理: 将一个图片每一个像素的颜色由其相邻的n*n个像素的平均值来替代。例如,将一个3*3的点阵,设带平滑的像素为f(i, j),平滑后为g(i, j),那么
f(i-1,j-1) f(i-1,j) f(i-1,j+1)
f(i,j-1) f(i,j) f(i,j+1)
f(i+1,j-1) f(i+1,j) f(i+1,j+1)
g(i,j)=( f(i-1,j-1) + f(i-1,j) + f(i-1,j+1) + f(i,j-1) + f(i,j) + f(i,j+1) + f(i+1,j-1) + f(i+1,j) + f(i+1,j+1) ) / 9
这里要注意的是对于边缘的像素的情况,防止越界。
彩色图像的霓虹处理: 同样以上面的3*3的点阵为例,目标像素g(i,j)应当以f(i,j)与f(i,j+1),f(i,j)与f(i+1,j)的梯度作为R,G,B分量,我们不妨设f(i,j)的RGB分量为(r1, g1, b1), f(i,j+1)为(r2, g2, b2), f(i+1,j)为(r3, g3, b3), g(i, j)为(r, g, b),那么结果应该为
r = 2 * sqrt( (r1 - r2)^2 + (r1 - r3)^2 )
g = 2 * sqrt( (g1 - g2)^2 + (g1 - g3)^2 )
b = 2 * sqrt( (b1 - b2)^2 + (b1 - b3)^2 )
彩色图像的锐化处理: 设f(i,j)像素为(r1, g1, b1) , f(i-1,j-1)像素为(r2,g2,b2), g(i,j)像素为(r,g,b),则
r = r1 + 0.25 * |r1 - r2|
g = g1 + 0.25 * |g1 - g2|
b = b1 + 0.25 * |b1 - b2|
彩色图像的浮雕处理: g(i, j) = f(i, j) - f(i - 1, j) + 常数 , 这里的常数通常选作128
彩色图像的镶嵌处理: 与彩色图像的平滑处理类似,但是不同的地方在于3*3的目标像素点都取作g(i,j),而不是另外的再去取所在矩阵像素的平均值。
彩色图像的灰度处理: r = r1 / 64 * 64 g = g1 / 64 * 64 b = b1 / 64 * 64 注意这里的除法是程序设计当中的整数除法。
5) 图象的几何变换:平移,缩放,旋转等均于解析几何当中的保持一致。
6) 图象的滤波处理
● 卷积滤波 原理是 y(n1, n2)=∑∑x(m1,m2)h(n1-m1,n2-m2) (两个求和符号的范围分别是 m1:0~N m2:0~N)
其中x(m1,m2)为输入图像信号,h(n1-m1,n2-m2)为滤波系统对单位采样序列δ(n1,n2)的响应。
⊙低通滤波 一般而言,图像中的噪声频谱位于空间频率较高的区域,空间域低通滤波用于平滑噪声。常用低通滤波的
h(n1, n2) 的3*3阵列如下:
1/9 1/9 1/9
h(n1, n2) = 1/9 1/9 1/9
1/9 1/9 1/9
1/10 1/10 1/10
h(n1, n2) = 1/10 2/10 1/10
1/10 1/10 1/10
1/16 1/8 1/16
h(n1, n2) = 1/8 1/4 1/8
1/16 1/8 1/16
采用5*5阵列低通滤波h(n1,n2)如下:
1/35 1/35 1/35 1/35 1/35
1/35 2/35 2/35 2/35 1/35
h(n1, n2) = 1/35 2/35 3/35 2/35 1/35
1/35 2/35 2/35 2/35 1/35
1/35 1/35 1/35 1/35 1/35
⊙高通滤波 空域高通滤波是对图像的低频分量进行拟制,让图像的高频分量无损耗或者低损耗的通过。空域高通滤波常用的h(n1,n2)的如下:
0 -1 0
h(n1, n2) = -1 5 -1
0 -1 0
-1 -1 -1
h(n1, n2) = -1 9 -1
-1 -1 -1
1 -2 1
h(n1, n2) = -2 5 -2
0 -2 1
● 增强处理
⊙ 水平增强 增强图像水平方向线条也是一种高通滤波。水平增强的h(n1, n2)的例子如下:
0 0 0
h(n1, n2) = 0 0 0
-1 2 -1
⊙ 垂直增强 增强图像垂直方向线条也是一种高通滤波。水平增强的h(n1, n2)的例子如下:
-1 0 0
h(n1, n2) = 2 0 0
-1 0 0
⊙ 水平垂直增强 水平垂直增强图像也是一种高通滤波。水平增强的h(n1, n2)的例子如下:
-1 -1 -1
h(n1, n2) = -1 8 -1
-1 -1 -1
● 结构滤波
⊙ 并联型结构滤波
结构如图: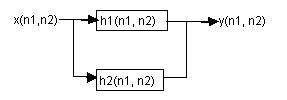
例如,当
0 0 0
h1(n1, n2) = 0 0 0
-1 2 -1
-1 0 0
h2(n1, n2) = 2 0 0
-1 0 0
则h(n1, n2)为
-1 0 0
h(n1, n2) = 2 0 0
-1 2 -1
⊙ 串联型结构滤波
结构如图:![]()
例如,当
0 0 0
h1(n1, n2) = 0 0 0
-1 2 -1
-1 0 0
h2(n1, n2) = 2 0 0
-1 0 0
则h(n1, n2)为
1 -2 1
h(n1, n2) = -2 4 -2
1 -2 1
7) 图象的切换特效处理
● 上部和下部对接显示
只需要不断的同时描绘对称的上部和下部的一行像素即可
● 左部和右部对接显示
只需要不断的同时描绘对称的左部和右部的一列像素即可
● 四边向中央显示
只需要不断的同时等进阶的描绘四边直至描绘到中心点即可
● 中央向四边显示
只需要不断的从中心点同时等进阶的描绘四边直至描绘到边缘即可
● 四角向中心显示
从左上角,右下角分别同时沿着主对角线等进阶的描绘自己所在像素的行,列像素直至中心
● 水平删条
设定分割长度L, 然后分别从高度为L, 2L, 3L ... 处等进阶的描绘行像素,显然这里进阶所需描绘高度为L
● 垂直删条
设定分割长度L, 然后分别从宽度为L, 2L, 3L ... 处等进阶的描绘列像素,显然这里进阶所需描绘宽度为L
● 由左向右(由右向左)
分别从左至右(从右至左)不断的描绘列像素直至边缘
● 由上向下(由下向上)
分别由上向下(由下向上)不断的描绘行像素直至边缘
8) 边缘探测
在图像测量,模式识别时,从图像中抽出线条,检测出图像边缘或者抽出图像轮廓是最常用的操作。迄今为止,已经出现了许多成熟的算法。例如微分算法,掩模算法等。在微分算法中,常使用N*N的像素块,例如3*3或者4*4。3*3的像素块如下,
f(i-1,j-1) f(i-1,j) f(i-1,j+1)
f(i,j-1) f(i,j) f(i,j+1)
f(i+1,j-1) f(i+1,j) f(i+1,j+1)
我们不妨设f(i,j)为待处理的像素,而g(i, j)为处理后的像素。
● Roberts算子
g(i, j) = sqrt( (f(i, j) - f(i + 1, j))^2 + (f(i + 1, j) - f(i, j + 1))^2 )
或者
g(i, j) = |f(i,j) - f(i + 1,j)| + |f(i+1,j) - f(i,j+1)|
● Sobel算子
对数字图像的每一个像素f(i,j),考察它的上、下、左、右邻域灰度的加权值,把各方向上(0度、45度、90度、135度)的灰度值加权之和作为输出,可以达到提取图像边缘的效果。
即 g(i,j) = fxr + fyr, 其中
fxr = f(i-1,j-1)+2*f(i-1,j)+f(i-1,j+1)-f(i+1,j-1)-2*f(i+1,j)-f(i+1,j+1)
fyr = f(i-1,j-1)+2*f(i,j-1)+f(i+1,j-1)-f(i-1,j+1)-2*f(i,j+1)-f(i+1,j+1)
● Laplace算子
Laplace算子是一种二阶微分算子。它有两种形式:4邻域微分算子和8邻域微分算子。
⊙ 4邻域微分
g(i,j)=|4*f(i,j)-f(i,j-1)-f(i-1,j)-f(i+1,j)-f(i,j+1)|
⊙ 8邻域微分
g(i,j)=|8*f(i,j)-f(i,j-1)-f(i-1,j)-f(i+1,j)-f(i,j+1)-f(i-1,j-1)-f(i-1,j+1)-f(i+1,j-1)-f(i+1,j+1)|
● 其他常用算子
⊙ 右下边缘抽出
采用3*3算子时,表达式为
g(i,j)=|-2*f(i,j-1)-2*f(i-1,j)+2*f(i+1,j)+2*f(i,j+1)|
⊙ prewitt 边缘探测样板算子
prewitt算子是一个边缘模板算子,由八个方向的样板组成,能够在0度,45度,90度,135度,180度,225度角
等八个方向检测边缘。8个3*3边缘模板及方向如下:
90度角: 45度角:
1 1 1 -1 -1 -1
1 -2 1 1 -2 1
-1 -1 -1 1 1 1
0度角: 315度角:
-1 1 1 1 1 -1
-1 -2 1 1 -2 -1
-1 1 1 1 1 -1
270度角: 225度角:
1 1 1 -1 -1 1
-1 -2 1 -1 -2 1
-1 -1 1 1 1 1
180度角: 135度角:
1 1 1 1 -1 -1
1 -2 -1 1 -2 -1
1 -1 -1 1 1 1
3*3时表达式如下:
A1*f(i-1,j-1) A8*f(i,j-1) A7*f(i+1,j-1)
A2*f(i-1,j) -2*f(i,j) A6*f(i+1, j)
A3*f(i-1,j+1) A4*f(i,j+1) A5*f(i+1,j+1)
g(i,j)=|-2*f(i,j)+A8*f(i,j-1)+A1*f(i-1,j-1)+A2*f(i-1,j)+A3*f(i-1,j+1)+A4*f(i,j+1)+A5*f(i+1,j+1)+A6*f(i+1,j)+A7*f(i+1,j-1)|
在程序设计中,依次用样板去检测图像,与被检测区域最为相似的样板给出最大值,用该最大值作为算子的输出值。
⊙ Robinson算子
Robinson算子是一个模板算子,由八个方向的样板组成,能够在0度,45度,90度,135度,180度,225度角
等八个方向检测边缘。8个3*3边缘模板及方向如下:
90度角: 45度角:
1 2 1 0 1 2
0 0 0 -1 0 1
-1 -2 -1 -2 -1 0
0度角: 315度角:
-1 0 1 -2 -1 0
-2 0 2 -1 0 1
-1 0 1 0 1 2
270度角: 225度角:
-1 -2 -1 0 -1 -2
0 0 0 1 0 -1
1 2 1 2 1 0
180度角: 135度角:
1 0 -1 2 1 0
2 0 -2 1 0 -1
1 0 -1 0 -1 -2
使用方法与prewitt算子一样。
⊙ Kirsch算子
Kirsch算子是一个模板算子,由八个方向的边缘样板组成,能够在0度,45度,90度,135度,180度,225度角
等八个方向检测边缘。8个3*3边缘模板及方向如下:
90度角: 45度角:
5 5 5 -3 5 5
-3 0 -3 -3 0 5
-3 -3 -3 -3 -3 -3
0度角: 315度角:
-3 -3 5 -3 -3 -3
-3 0 5 -3 0 5
-3 -3 5 -3 5 5
270度角: 225度角:
5 5 -3 -3 -3 -3
5 0 -3 5 0 -3
-3 -3 -3 5 5 -3
180度角: 135度角:
5 -3 -3 5 5 -3
5 0 -3 5 0 -3
5 -3 -3 -3 -3 3
使用方法与prewitt算子一样。
⊙ Smoothed算子
Smoothed算子是一个3*3的算子,设
|-1 0 1| |1 1 1|
Dx = |-1 0 1| Dy = |0 0 0|
|-1 0 1| |-1 -1 -1|
则 D = sqrt(Dx^2 + Dy^2) 或者 D = |Dx| + |Dy|
或 Dx(i, j) = f(i-1,j+1)+f(i,j+1)+f(i+1,j+1)-f(i-1,j-1)-f(i,j-1)-f(i+1,j-1)
Dy(i,j) = f(i-1,j-1)+f(i-1,j)+f(i-1,j+1)-f(i+1,j-1)-f(i+1,j)-f(i+1,j+1)
9) 灰度图像处理
所谓灰度处理是根据单色图像的灰度对输出图像的灰度进行再定义、以改善图像的对比度。单色图像的灰度有256级、128级、64级等,下面均以256级单色图像举例。
我们不妨设源图像的灰度值为f(i,j),处理后的灰度值为g(i,j)
● 逆反处理
与彩色图像的逆反处理一样: g(i,j) = 255 - f(i,j)
● 灰度级切换
灰度级切换的输入、输出灰度值对应关系如下: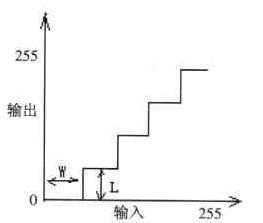
● 增大对比度
输入的灰度值越高,对应的输出灰度值越低。灰度值减少,图像变暗,从而使对比度增加。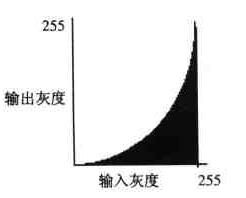
● 减小对比度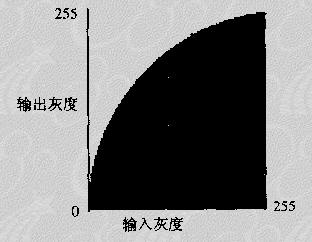
● 改善对比度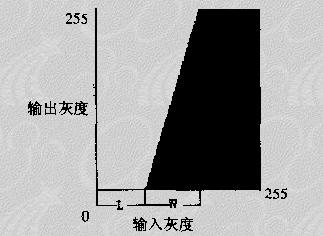
● 增强对比度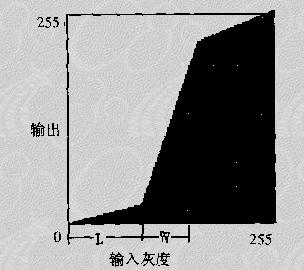
● 局部滤波处理
局部滤波处理是指利用3*3的图像块内的像素的颜色值对当前像素进行设定的一种图像处理技术。
⊙ 平均值滤波
与彩色图像平滑处理类似。
g(i,j)=( f(i-1,j-1) + f(i-1,j) + f(i-1,j+1) + f(i,j-1) + f(i,j) + f(i,j+1) + f(i+1,j-1) + f(i+1,j) + f(i+1,j+1) ) / 9
这里要注意的是对于边缘的像素的情况,防止越界。
⊙ 最小值滤波
最小值滤波是指在图像中以当前像素f(i,j)为中心切出一个N*M(例如3*3)像素组成的图像块,g(i,j)取图像块中灰度值中的最小值
⊙ 最大值滤波
最大值滤波是指在图像中以当前像素f(i,j)为中心切出一个N*M(例如3*3)像素组成的图像块,g(i,j)取图像块中灰度值中的最大值
⊙ 中值滤波
中值滤波是指在图像中以当前像素f(i,j)为中心切出一个N*M(例如3*3)像素组成的图像块,g(i,j)取图像块中所有灰度排序后序列的中间值
10) 灰度图像处理
● 灰度图像的二值化
⊙ 灰度图像直方图
对于每个灰度值,求出在图像中具有该灰度值的像素数的图形叫做灰度直方图。。灰度直方图是灰度级的函数,描述图像中具有相同灰度像素的个数。灰度直方图的横坐标是灰度级,纵坐标是该灰度出现的频率(即像素的个数)。直方图的用途主要是给出了一个简单可见的指示,用来判断一幅图像是否合理的利用了全部被允许的灰度级范围。一般一幅数字图像应该利用全部或几乎全部可能的灰度级范围。一般一幅数字图像应该利用全部或几乎全部可能的灰度级,否则增加了量化间隔。一旦被数字化图像的级数小于255,丢失的信息将不能恢复。如果图像具有超出数字量化器所能处理的范围的亮度,则这些灰度级将简单的置为0或255,由此将在直方图的一端或两端产生尖峰。灰度图像直方图具有直方图的一些统计特征参量,包括了灰度最大值,灰度最小值,均值和标准差。
⊙ 阙值计算和图像二值化
图像二值化的阙值处理方式为:
g(i,j) = 1; f(i,j)>=t
g(i,j) = 0; f(i,j)<t
通常,用g(i,j)=1表示图像,用g(i,)=0表示背景。确定t的方法叫做阙值选择。
● 灰度图像的二值化算法
⊙ 类判别法寻找阙值的步骤:
(1) 计算输入图像的灰度级直方图(用灰度级的概率函数PHS(i)来表示)
(2) 计算灰度均值(Ave) Ave = sigma((i - 1)*Phs(i)) i: 0->255
(3) 计算灰度类均值(Aver(k))和类直方图和(W(k))
Aver(k) = sigma((i+1)*Phs(i)) i: 0->k
W(k) = sigma(Phs(i)) i: 1->k
(4)计算类分离指标
Q(k)={[Ave*W(k)-Aver(k)]^2)}/[W(k)*(1-W(k))]}
(5) 求使Q最大的k 最佳阙值: T = k - 1
⊙ 灰度级切片法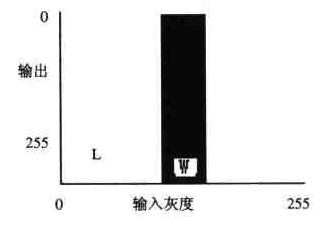
将输入图像的某一灰度级范围内的所有像素全部置为0(黑),其余灰度级的所有像素全部置为255(白),则生成黑白
二值图像。
⊙ 等灰度片二值化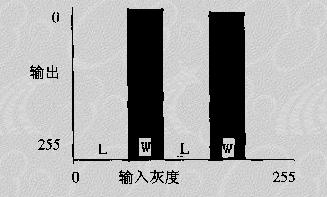
将输入图像在某两个等宽的灰度级范围内的所有像素全部置为0(黑),其余灰度级的所有像素全部置为255(白),则生成黑白二值图像。
⊙ 线性二值化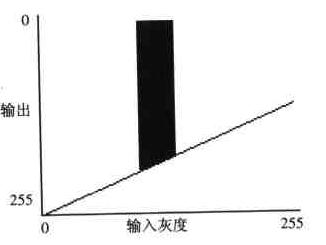
将输入图像在某一灰度级内的所有像素全部置为0(黑),其余灰度级的所有像素全部置为原值的1/2,则生成黑白二值图像,并将图像与背景分离。
● 二值图像处理
二值图像处理是指将二值化的图像进行某种修正,使之更适合于图像测量。二值图像处理包括以下操作:
膨胀 使粒子变大。对图像进行膨胀处理之后再进行收缩处理,则可以修正图像的凹槽
收缩 使粒子变小。对图像进行收缩处理之后再进行膨胀处理,则可以修正图像的凸槽
清除孤立点 清除由一个像素构成的对象以及修正由一个像素构成的孔。
清除粒子 清除任意面积以下的对象
清除超大粒子 清除任意面积以上的对象
洞穴填充 填充任意范围
⊙ 4邻域收缩
4邻域收缩的原理是,在3*3的图像块中,如果当前处理像素f(i,j)为0,则其相邻的像素f(i,j+1),f(i,j-1),f(i-1,j),f(i+1,j)均置255。
⊙ 8邻域收缩
8邻域收缩的原理是,在3*3的图像块中,如果当前处理像素f(i,j)为0,则其相邻的像素f(i,j+1),f(i,j-1),f(i-1,j),f(i+1,j),f(i-1,j-1),f(i+1,j-1),f(i-1,j+1),f(i+1,j+1)均置255。
⊙ 4邻域膨胀
4邻域膨胀的原理是,在3*3的图像块中,如果当前处理像素f(i,j)为1,则其相邻的像素f(i,j+1),f(i,j-1),f(i-1,j),f(i+1,j)均置1。
⊙ 8邻域膨胀
8邻域膨胀的原理是,在3*3的图像块中,如果当前处理像素f(i,j)为1,则其相邻的像素f(i,j+1),f(i,j-1),f(i-1,j),f(i+1,j),f(i-1,j-1),f(i+1,j-1),f(i-1,j+1),f(i+1,j+1)均置1。
⊙ 8邻域清除孤立点
8邻域清除孤立点的原理是,在3*3的图像块中,如果当前处理像素f(i,j)为1,而其相邻的像素f(i,j+1),f(i,j-1),f(i-1,j),f(i+1,j),f(i-1,j-1),f(i+1,j-1),f(i-1,j+1),f(i+1,j+1)均为0时,当前处理像素f(i,j)为0。
⊙ 4邻域清除孤立点
4邻域清除孤立点的原理是,在3*3的图像块中,如果当前处理像素f(i,j)为1,而其相邻的像素f(i,j+1),f(i,j-1),f(i-1,j),f(i+1,j均为0时,当前处理像素f(i,j)为0。