一元二次、一元三次、一元四次方程的求根公式

代码用python写的。

一元二次方程：

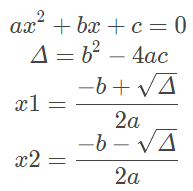
def Quadratic(args):
    a,b,c=args
    D = cmath.sqrt(b**2-4*a*c)
    x1 = (-b+D)/(2*a)
    x2 = (-b-D)/(2*a)
    roots = [x1,x2]
    return roots

一元三次方程：

 

 

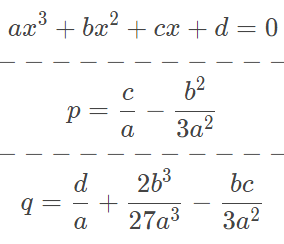
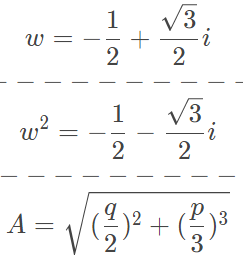
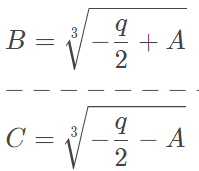
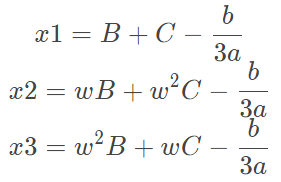
def Cubic(args):
    a,b,c,d = args
    p = c/a-b**2/(3*a**2)
    q = d/a+2*b**3/(27*a**3)-b*c/(3*a**2)
    w = complex(-0.5,(3**0.5)/2)
    ww = complex(-0.5,-(3**0.5)/2)
    A = cmath.sqrt((q/2)**2+(p/3)**3)
    B = ThreeSquare(-q/2+A)
    C = ThreeSquare(-q/2-A)
    y1 = B+C
    y2 = w*B+ww*C
    y3 = ww*B+w*C
    D = b/(3*a)
    roots=[RoundAns(y1-D,6),RoundAns(y2-D,6),RoundAns(y3-D,6)]
    return roots

一元四次方程：

 

 

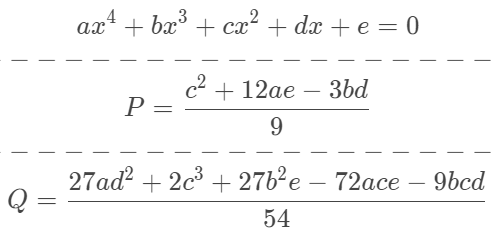
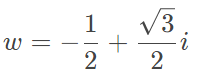
for k=0,1,2,计算m

 如果三个m的值都为0，则

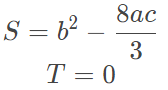
 否则的话，取|m|最大的那个k，并计算

 

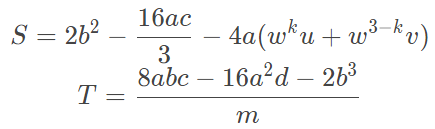
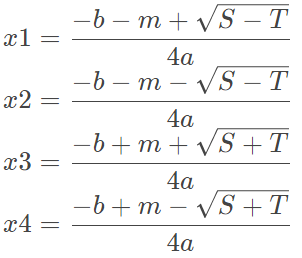
def Quartic(args):
    a,b,c,d,e = args
    P = (c**2+12*a*e-3*b*d)/9
    Q = (27*a*d**2+2*c**3+27*b**2*e-72*a*c*e-9*b*c*d)/54
    D = cmath.sqrt(Q**2-P**3)
    u = ThreeSquare(Q+D) if abs(Q+D)>=abs(Q-D) else ThreeSquare(Q-D)
    v = 0 if u==0 else P/u
    w = complex(-0.5,3**0.5/2)
    m = []
    M = []
    flag = 0
    roots = []
    for i in range(3):
        x = cmath.sqrt(b**2-8*a*c/3+4*a*(w**i*u+w**(3-i)*v))
        m.append(x)
        M.append(abs(x))
        if m == 0:
            flag=flag+1
    if flag == 3:
        mm = 0
        S = b**2-8*a*c/3
        T = 0
    else:
        t = M.index(max(M))
        mm = m[t]
        S = 2*b**2-16*a*c/3-4*a*(w**t*u+w**(3-t)*v)
        T = (8*a*b*c-16*a**2*d-2*b**3)/mm
    x1=(-b-mm+cmath.sqrt(S-T))/(4*a)
    x2=(-b-mm-cmath.sqrt(S-T))/(4*a)
    x3=(-b+mm+cmath.sqrt(S+T))/(4*a)
    x4=(-b+mm-cmath.sqrt(S+T))/(4*a)
    roots.append(x1)
    roots.append(x2)
    roots.append(x3)
    roots.append(x4)
        
    return roots

完整代码见：

https://github.com/Larissa1990/Solve-cubic-and-quartic-equations-with-one-unknown/blob/master/README.md