如何计算微分

Ceres为google开源非线性优化库。

计算微分方法

• 符号微分  Analytic Derivative
• 数值微分  Numeric Derivative

Forward Difference

Central Difference

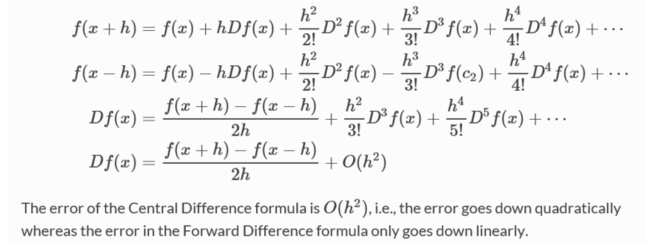
Ridders’ Method

• 自动微分Automatic Derivative

自动微分可以精确快速的算出微分值。

// Ceres Solver - A fast non-linear least squares minimizer
// Copyright 2015 Google Inc. All rights reserved.
// http://ceres-solver.org/
//
// Redistribution and use in source and binary forms, with or without
// modification, are permitted provided that the following conditions are met:
//
// * Redistributions of source code must retain the above copyright notice,
//   this list of conditions and the following disclaimer.
// * Redistributions in binary form must reproduce the above copyright notice,
//   this list of conditions and the following disclaimer in the documentation
//   and/or other materials provided with the distribution.
// * Neither the name of Google Inc. nor the names of its contributors may be
//   used to endorse or promote products derived from this software without
//   specific prior written permission.
//
// THIS SOFTWARE IS PROVIDED BY THE COPYRIGHT HOLDERS AND CONTRIBUTORS "AS IS"
// AND ANY EXPRESS OR IMPLIED WARRANTIES, INCLUDING, BUT NOT LIMITED TO, THE
// IMPLIED WARRANTIES OF MERCHANTABILITY AND FITNESS FOR A PARTICULAR PURPOSE
// ARE DISCLAIMED. IN NO EVENT SHALL THE COPYRIGHT OWNER OR CONTRIBUTORS BE
// LIABLE FOR ANY DIRECT, INDIRECT, INCIDENTAL, SPECIAL, EXEMPLARY, OR
// CONSEQUENTIAL DAMAGES (INCLUDING, BUT NOT LIMITED TO, PROCUREMENT OF
// SUBSTITUTE GOODS OR SERVICES; LOSS OF USE, DATA, OR PROFITS; OR BUSINESS
// INTERRUPTION) HOWEVER CAUSED AND ON ANY THEORY OF LIABILITY, WHETHER IN
// CONTRACT, STRICT LIABILITY, OR TORT (INCLUDING NEGLIGENCE OR OTHERWISE)
// ARISING IN ANY WAY OUT OF THE USE OF THIS SOFTWARE, EVEN IF ADVISED OF THE
// POSSIBILITY OF SUCH DAMAGE.
//
// Author: keir@google.com (Keir Mierle)
//
// A simple implementation of N-dimensional dual numbers, for automatically
// computing exact derivatives of functions.
//
// While a complete treatment of the mechanics of automatic differentiation is
// beyond the scope of this header (see
// http://en.wikipedia.org/wiki/Automatic_differentiation for details), the
// basic idea is to extend normal arithmetic with an extra element, "e," often
// denoted with the greek symbol epsilon, such that e != 0 but e^2 = 0. Dual
// numbers are extensions of the real numbers analogous to complex numbers:
// whereas complex numbers augment the reals by introducing an imaginary unit i
// such that i^2 = -1, dual numbers introduce an "infinitesimal" unit e such
// that e^2 = 0. Dual numbers have two components: the "real" component and the
// "infinitesimal" component, generally written as x + y*e. Surprisingly, this
// leads to a convenient method for computing exact derivatives without needing
// to manipulate complicated symbolic expressions.
//
// For example, consider the function
//
//   f(x) = x^2 ,
//
// evaluated at 10. Using normal arithmetic, f(10) = 100, and df/dx(10) = 20.
// Next, argument 10 with an infinitesimal to get:
//
//   f(10 + e) = (10 + e)^2
//             = 100 + 2 * 10 * e + e^2
//             = 100 + 20 * e       -+-
//                     --            |
//                     |             +--- This is zero, since e^2 = 0
//                     |
//                     +----------------- This is df/dx!
//
// Note that the derivative of f with respect to x is simply the infinitesimal
// component of the value of f(x + e). So, in order to take the derivative of
// any function, it is only necessary to replace the numeric "object" used in
// the function with one extended with infinitesimals. The class Jet, defined in
// this header, is one such example of this, where substitution is done with
// templates.
//
// To handle derivatives of functions taking multiple arguments, different
// infinitesimals are used, one for each variable to take the derivative of. For
// example, consider a scalar function of two scalar parameters x and y:
//
//   f(x, y) = x^2 + x * y
//
// Following the technique above, to compute the derivatives df/dx and df/dy for
// f(1, 3) involves doing two evaluations of f, the first time replacing x with
// x + e, the second time replacing y with y + e.
//
// For df/dx:
//
//   f(1 + e, y) = (1 + e)^2 + (1 + e) * 3
//               = 1 + 2 * e + 3 + 3 * e
//               = 4 + 5 * e
//
//               --> df/dx = 5
//
// For df/dy:
//
//   f(1, 3 + e) = 1^2 + 1 * (3 + e)
//               = 1 + 3 + e
//               = 4 + e
//
//               --> df/dy = 1
//
// To take the gradient of f with the implementation of dual numbers ("jets") in
// this file, it is necessary to create a single jet type which has components
// for the derivative in x and y, and passing them to a templated version of f:
//
//   template<typename T>
//   T f(const T &x, const T &y) {
//     return x * x + x * y;
//   }
//
//   // The "2" means there should be 2 dual number components.
//   // It computes the partial derivative at x=10, y=20.
//   Jet<double, 2> x(10, 0);  // Pick the 0th dual number for x.
//   Jet<double, 2> y(20, 1);  // Pick the 1st dual number for y.
//   Jet<double, 2> z = f(x, y);
//
//   LOG(INFO) << "df/dx = " << z.v[0]
//             << "df/dy = " << z.v[1];
//
// Most users should not use Jet objects directly; a wrapper around Jet objects,
// which makes computing the derivative, gradient, or jacobian of templated
// functors simple, is in autodiff.h. Even autodiff.h should not be used
// directly; instead autodiff_cost_function.h is typically the file of interest.
//
// For the more mathematically inclined, this file implements first-order
// "jets". A 1st order jet is an element of the ring
//
//   T[N] = T[t_1, ..., t_N] / (t_1, ..., t_N)^2
//
// which essentially means that each jet consists of a "scalar" value 'a' from T
// and a 1st order perturbation vector 'v' of length N:
//
//   x = a + sum_i v[i] t_i
//
// A shorthand is to write an element as x = a + u, where u is the perturbation.
// Then, the main point about the arithmetic of jets is that the product of
// perturbations is zero:
//
//   (a + u) * (b + v) = ab + av + bu + uv
//                     = ab + (av + bu) + 0
//
// which is what operator* implements below. Addition is simpler:
//
//   (a + u) + (b + v) = (a + b) + (u + v).
//
// The only remaining question is how to evaluate the function of a jet, for
// which we use the chain rule:
//
//   f(a + u) = f(a) + f'(a) u
//
// where f'(a) is the (scalar) derivative of f at a.
//
// By pushing these things through sufficiently and suitably templated
// functions, we can do automatic differentiation. Just be sure to turn on
// function inlining and common-subexpression elimination, or it will be very
// slow!
//
// WARNING: Most Ceres users should not directly include this file or know the
// details of how jets work. Instead the suggested method for automatic
// derivatives is to use autodiff_cost_function.h, which is a wrapper around
// both jets.h and autodiff.h to make taking derivatives of cost functions for
// use in Ceres easier.

#ifndef CERES_PUBLIC_JET_H_
#define CERES_PUBLIC_JET_H_

#include <cmath>
#include <iosfwd>
#include <iostream>  // NOLINT
#include <limits>
#include <string>

#include "Eigen/Core"
//////#include "ceres/internal/port.h"

namespace ceres {

    template <typename T, int N>
    struct Jet {
        enum { DIMENSION = N };
        typedef T Scalar;

        // Default-construct "a" because otherwise this can lead to false errors about
        // uninitialized uses when other classes relying on default constructed T
        // (where T is a Jet<T, N>). This usually only happens in opt mode. Note that
        // the C++ standard mandates that e.g. default constructed doubles are
        // initialized to 0.0; see sections 8.5 of the C++03 standard.
        Jet() : a() {
            v.setZero();
        }

        // Constructor from scalar: a + 0.
        explicit Jet(const T& value) {
            a = value;
            v.setZero();
        }

        // Constructor from scalar plus variable: a + t_i.
        Jet(const T& value, int k) {
            a = value;
            v.setZero();
            v[k] = T(1.0);
        }

        // Constructor from scalar and vector part
        // The use of Eigen::DenseBase allows Eigen expressions
        // to be passed in without being fully evaluated until
        // they are assigned to v
        template<typename Derived>
        EIGEN_STRONG_INLINE Jet(const T& a, const Eigen::DenseBase<Derived> &v)
            : a(a), v(v) {
        }

        // Compound operators
        Jet<T, N>& operator+=(const Jet<T, N> &y) {
            *this = *this + y;
            return *this;
        }

        Jet<T, N>& operator-=(const Jet<T, N> &y) {
            *this = *this - y;
            return *this;
        }

        Jet<T, N>& operator*=(const Jet<T, N> &y) {
            *this = *this * y;
            return *this;
        }

        Jet<T, N>& operator/=(const Jet<T, N> &y) {
            *this = *this / y;
            return *this;
        }

        // Compound with scalar operators.
        Jet<T, N>& operator+=(const T& s) {
            *this = *this + s;
            return *this;
        }

        Jet<T, N>& operator-=(const T& s) {
            *this = *this - s;
            return *this;
        }

        Jet<T, N>& operator*=(const T& s) {
            *this = *this * s;
            return *this;
        }

        Jet<T, N>& operator/=(const T& s) {
            *this = *this / s;
            return *this;
        }

        // The scalar part.
        T a;

        // The infinitesimal part.
        //
        // We allocate Jets on the stack and other places they might not be aligned
        // to X(=16 [SSE], 32 [AVX] etc)-byte boundaries, which would prevent the safe
        // use of vectorisation.  If we have C++11, we can specify the alignment.
        // However, the standard gives wide latitude as to what alignments are valid,
        // and it might be that the maximum supported alignment *guaranteed* to be
        // supported is < 16, in which case we do not specify an alignment, as this
        // implies the host is not a modern x86 machine.  If using < C++11, we cannot
        // specify alignment.

#if defined(EIGEN_DONT_VECTORIZE)
        Eigen::Matrix<T, N, 1, Eigen::DontAlign> v;
#else
        // Enable vectorisation iff the maximum supported scalar alignment is >=
        // 16 bytes, as this is the minimum required by Eigen for any vectorisation.
        //
        // NOTE: It might be the case that we could get >= 16-byte alignment even if
        //       max_align_t < 16.  However we can't guarantee that this
        //       would happen (and it should not for any modern x86 machine) and if it
        //       didn't, we could get misaligned Jets.
        static constexpr int kAlignOrNot =
            // Work around a GCC 4.8 bug
            // (https://gcc.gnu.org/bugzilla/show_bug.cgi?id=56019) where
            // std::max_align_t is misplaced.
#if defined (__GNUC__) && __GNUC__ == 4 && __GNUC_MINOR__ == 8
            alignof(::max_align_t) >= 16
#else
            alignof(std::max_align_t) >= 16
#endif
            ? Eigen::AutoAlign : Eigen::DontAlign;

#if defined(EIGEN_MAX_ALIGN_BYTES)
        // Eigen >= 3.3 supports AVX & FMA instructions that require 32-byte alignment
        // (greater for AVX512).  Rather than duplicating the detection logic, use
        // Eigen's macro for the alignment size.
        //
        // NOTE: EIGEN_MAX_ALIGN_BYTES can be > 16 (e.g. 32 for AVX), even though
        //       kMaxAlignBytes will max out at 16.  We are therefore relying on
        //       Eigen's detection logic to ensure that this does not result in
        //       misaligned Jets.
#define CERES_JET_ALIGN_BYTES EIGEN_MAX_ALIGN_BYTES
#else
        // Eigen < 3.3 only supported 16-byte alignment.
#define CERES_JET_ALIGN_BYTES 16
#endif

        // Default to the native alignment if 16-byte alignment is not guaranteed to
        // be supported.  We cannot use alignof(T) as if we do, GCC 4.8 complains that
        // the alignment 'is not an integer constant', although Clang accepts it.
        static constexpr size_t kAlignment = kAlignOrNot == Eigen::AutoAlign
            ? CERES_JET_ALIGN_BYTES : alignof(double);

#undef CERES_JET_ALIGN_BYTES
        alignas(kAlignment)Eigen::Matrix<T, N, 1, kAlignOrNot> v;
#endif
    };

    // Unary +
    template<typename T, int N> inline
        Jet<T, N> const& operator+(const Jet<T, N>& f) {
        return f;
    }

    // TODO(keir): Try adding __attribute__((always_inline)) to these functions to
    // see if it causes a performance increase.

    // Unary -
    template<typename T, int N> inline
        Jet<T, N> operator-(const Jet<T, N>&f) {
        return Jet<T, N>(-f.a, -f.v);
    }

    // Binary +
    template<typename T, int N> inline
        Jet<T, N> operator+(const Jet<T, N>& f,
            const Jet<T, N>& g) {
        return Jet<T, N>(f.a + g.a, f.v + g.v);
    }

    // Binary + with a scalar: x + s
    template<typename T, int N> inline
        Jet<T, N> operator+(const Jet<T, N>& f, T s) {
        return Jet<T, N>(f.a + s, f.v);
    }

    // Binary + with a scalar: s + x
    template<typename T, int N> inline
        Jet<T, N> operator+(T s, const Jet<T, N>& f) {
        return Jet<T, N>(f.a + s, f.v);
    }

    // Binary -
    template<typename T, int N> inline
        Jet<T, N> operator-(const Jet<T, N>& f,
            const Jet<T, N>& g) {
        return Jet<T, N>(f.a - g.a, f.v - g.v);
    }

    // Binary - with a scalar: x - s
    template<typename T, int N> inline
        Jet<T, N> operator-(const Jet<T, N>& f, T s) {
        return Jet<T, N>(f.a - s, f.v);
    }

    // Binary - with a scalar: s - x
    template<typename T, int N> inline
        Jet<T, N> operator-(T s, const Jet<T, N>& f) {
        return Jet<T, N>(s - f.a, -f.v);
    }

    // Binary *
    template<typename T, int N> inline
        Jet<T, N> operator*(const Jet<T, N>& f,
            const Jet<T, N>& g) {
        return Jet<T, N>(f.a * g.a, f.a * g.v + f.v * g.a);
    }

    // Binary * with a scalar: x * s
    template<typename T, int N> inline
        Jet<T, N> operator*(const Jet<T, N>& f, T s) {
        return Jet<T, N>(f.a * s, f.v * s);
    }

    // Binary * with a scalar: s * x
    template<typename T, int N> inline
        Jet<T, N> operator*(T s, const Jet<T, N>& f) {
        return Jet<T, N>(f.a * s, f.v * s);
    }

    // Binary /
    template<typename T, int N> inline
        Jet<T, N> operator/(const Jet<T, N>& f,
            const Jet<T, N>& g) {
        // This uses:
        //
        //   a + u   (a + u)(b - v)   (a + u)(b - v)
        //   ----- = -------------- = --------------
        //   b + v   (b + v)(b - v)        b^2
        //
        // which holds because v*v = 0.
        const T g_a_inverse = T(1.0) / g.a;
        const T f_a_by_g_a = f.a * g_a_inverse;
        return Jet<T, N>(f_a_by_g_a, (f.v - f_a_by_g_a * g.v) * g_a_inverse);
    }

    // Binary / with a scalar: s / x
    template<typename T, int N> inline
        Jet<T, N> operator/(T s, const Jet<T, N>& g) {
        const T minus_s_g_a_inverse2 = -s / (g.a * g.a);
        return Jet<T, N>(s / g.a, g.v * minus_s_g_a_inverse2);
    }

    // Binary / with a scalar: x / s
    template<typename T, int N> inline
        Jet<T, N> operator/(const Jet<T, N>& f, T s) {
        const T s_inverse = T(1.0) / s;
        return Jet<T, N>(f.a * s_inverse, f.v * s_inverse);
    }

    // Binary comparison operators for both scalars and jets.
#define CERES_DEFINE_JET_COMPARISON_OPERATOR(op) 
template<typename T, int N> inline 
bool operator op(const Jet<T, N>& f, const Jet<T, N>& g) { 
  return f.a op g.a; 
} 
template<typename T, int N> inline 
bool operator op(const T& s, const Jet<T, N>& g) { 
  return s op g.a; 
} 
template<typename T, int N> inline 
bool operator op(const Jet<T, N>& f, const T& s) { 
  return f.a op s; 
}
    CERES_DEFINE_JET_COMPARISON_OPERATOR(< )  // NOLINT
        CERES_DEFINE_JET_COMPARISON_OPERATOR(<= )  // NOLINT
        CERES_DEFINE_JET_COMPARISON_OPERATOR(> )  // NOLINT
        CERES_DEFINE_JET_COMPARISON_OPERATOR(>= )  // NOLINT
        CERES_DEFINE_JET_COMPARISON_OPERATOR(== )  // NOLINT
        CERES_DEFINE_JET_COMPARISON_OPERATOR(!= )  // NOLINT
#undef CERES_DEFINE_JET_COMPARISON_OPERATOR

                                                   // Pull some functions from namespace std.
                                                   //
                                                   // This is necessary because we want to use the same name (e.g. 'sqrt') for
                                                   // double-valued and Jet-valued functions, but we are not allowed to put
                                                   // Jet-valued functions inside namespace std.
        using std::abs;
    using std::acos;
    using std::asin;
    using std::atan;
    using std::atan2;
    using std::cbrt;
    using std::ceil;
    using std::cos;
    using std::cosh;
    using std::exp;
    using std::exp2;
    using std::floor;
    using std::fmax;
    using std::fmin;
    using std::hypot;
    using std::isfinite;
    using std::isinf;
    using std::isnan;
    using std::isnormal;
    using std::log;
    using std::log2;
    using std::pow;
    using std::sin;
    using std::sinh;
    using std::sqrt;
    using std::tan;
    using std::tanh;

    // Legacy names from pre-C++11 days.
    inline bool IsFinite(double x) { return std::isfinite(x); }
    inline bool IsInfinite(double x) { return std::isinf(x); }
    inline bool IsNaN(double x) { return std::isnan(x); }
    inline bool IsNormal(double x) { return std::isnormal(x); }

    // In general, f(a + h) ~= f(a) + f'(a) h, via the chain rule.

    // abs(x + h) ~= x + h or -(x + h)
    template <typename T, int N> inline
        Jet<T, N> abs(const Jet<T, N>& f) {
        return f.a < T(0.0) ? -f : f;
    }

    // log(a + h) ~= log(a) + h / a
    template <typename T, int N> inline
        Jet<T, N> log(const Jet<T, N>& f) {
        const T a_inverse = T(1.0) / f.a;
        return Jet<T, N>(log(f.a), f.v * a_inverse);
    }

    // exp(a + h) ~= exp(a) + exp(a) h
    template <typename T, int N> inline
        Jet<T, N> exp(const Jet<T, N>& f) {
        const T tmp = exp(f.a);
        return Jet<T, N>(tmp, tmp * f.v);
    }

    // sqrt(a + h) ~= sqrt(a) + h / (2 sqrt(a))
    template <typename T, int N> inline
        Jet<T, N> sqrt(const Jet<T, N>& f) {
        const T tmp = sqrt(f.a);
        const T two_a_inverse = T(1.0) / (T(2.0) * tmp);
        return Jet<T, N>(tmp, f.v * two_a_inverse);
    }

    // cos(a + h) ~= cos(a) - sin(a) h
    template <typename T, int N> inline
        Jet<T, N> cos(const Jet<T, N>& f) {
        return Jet<T, N>(cos(f.a), -sin(f.a) * f.v);
    }

    // acos(a + h) ~= acos(a) - 1 / sqrt(1 - a^2) h
    template <typename T, int N> inline
        Jet<T, N> acos(const Jet<T, N>& f) {
        const T tmp = -T(1.0) / sqrt(T(1.0) - f.a * f.a);
        return Jet<T, N>(acos(f.a), tmp * f.v);
    }

    // sin(a + h) ~= sin(a) + cos(a) h
    template <typename T, int N> inline
        Jet<T, N> sin(const Jet<T, N>& f) {
        return Jet<T, N>(sin(f.a), cos(f.a) * f.v);
    }

    // asin(a + h) ~= asin(a) + 1 / sqrt(1 - a^2) h
    template <typename T, int N> inline
        Jet<T, N> asin(const Jet<T, N>& f) {
        const T tmp = T(1.0) / sqrt(T(1.0) - f.a * f.a);
        return Jet<T, N>(asin(f.a), tmp * f.v);
    }

    // tan(a + h) ~= tan(a) + (1 + tan(a)^2) h
    template <typename T, int N> inline
        Jet<T, N> tan(const Jet<T, N>& f) {
        const T tan_a = tan(f.a);
        const T tmp = T(1.0) + tan_a * tan_a;
        return Jet<T, N>(tan_a, tmp * f.v);
    }

    // atan(a + h) ~= atan(a) + 1 / (1 + a^2) h
    template <typename T, int N> inline
        Jet<T, N> atan(const Jet<T, N>& f) {
        const T tmp = T(1.0) / (T(1.0) + f.a * f.a);
        return Jet<T, N>(atan(f.a), tmp * f.v);
    }

    // sinh(a + h) ~= sinh(a) + cosh(a) h
    template <typename T, int N> inline
        Jet<T, N> sinh(const Jet<T, N>& f) {
        return Jet<T, N>(sinh(f.a), cosh(f.a) * f.v);
    }

    // cosh(a + h) ~= cosh(a) + sinh(a) h
    template <typename T, int N> inline
        Jet<T, N> cosh(const Jet<T, N>& f) {
        return Jet<T, N>(cosh(f.a), sinh(f.a) * f.v);
    }

    // tanh(a + h) ~= tanh(a) + (1 - tanh(a)^2) h
    template <typename T, int N> inline
        Jet<T, N> tanh(const Jet<T, N>& f) {
        const T tanh_a = tanh(f.a);
        const T tmp = T(1.0) - tanh_a * tanh_a;
        return Jet<T, N>(tanh_a, tmp * f.v);
    }

    // The floor function should be used with extreme care as this operation will
    // result in a zero derivative which provides no information to the solver.
    //
    // floor(a + h) ~= floor(a) + 0
    template <typename T, int N> inline
        Jet<T, N> floor(const Jet<T, N>& f) {
        return Jet<T, N>(floor(f.a));
    }

    // The ceil function should be used with extreme care as this operation will
    // result in a zero derivative which provides no information to the solver.
    //
    // ceil(a + h) ~= ceil(a) + 0
    template <typename T, int N> inline
        Jet<T, N> ceil(const Jet<T, N>& f) {
        return Jet<T, N>(ceil(f.a));
    }

    // Some new additions to C++11:

    // cbrt(a + h) ~= cbrt(a) + h / (3 a ^ (2/3))
    template <typename T, int N> inline
        Jet<T, N> cbrt(const Jet<T, N>& f) {
        const T derivative = T(1.0) / (T(3.0) * cbrt(f.a * f.a));
        return Jet<T, N>(cbrt(f.a), f.v * derivative);
    }

    // exp2(x + h) = 2^(x+h) ~= 2^x + h*2^x*log(2)
    template <typename T, int N> inline
        Jet<T, N> exp2(const Jet<T, N>& f) {
        const T tmp = exp2(f.a);
        const T derivative = tmp * log(T(2));
        return Jet<T, N>(tmp, f.v * derivative);
    }

    // log2(x + h) ~= log2(x) + h / (x * log(2))
    template <typename T, int N> inline
        Jet<T, N> log2(const Jet<T, N>& f) {
        const T derivative = T(1.0) / (f.a * log(T(2)));
        return Jet<T, N>(log2(f.a), f.v * derivative);
    }

    // Like sqrt(x^2 + y^2),
    // but acts to prevent underflow/overflow for small/large x/y.
    // Note that the function is non-smooth at x=y=0,
    // so the derivative is undefined there.
    template <typename T, int N> inline
        Jet<T, N> hypot(const Jet<T, N>& x, const Jet<T, N>& y) {
        // d/da sqrt(a) = 0.5 / sqrt(a)
        // d/dx x^2 + y^2 = 2x
        // So by the chain rule:
        // d/dx sqrt(x^2 + y^2) = 0.5 / sqrt(x^2 + y^2) * 2x = x / sqrt(x^2 + y^2)
        // d/dy sqrt(x^2 + y^2) = y / sqrt(x^2 + y^2)
        const T tmp = hypot(x.a, y.a);
        return Jet<T, N>(tmp, x.a / tmp * x.v + y.a / tmp * y.v);
    }

    template <typename T, int N> inline
        const Jet<T, N>& fmax(const Jet<T, N>& x, const Jet<T, N>& y) {
        return x < y ? y : x;
    }

    template <typename T, int N> inline
        const Jet<T, N>& fmin(const Jet<T, N>& x, const Jet<T, N>& y) {
        return y < x ? y : x;
    }

    // Bessel functions of the first kind with integer order equal to 0, 1, n.
    //
    // Microsoft has deprecated the j[0,1,n]() POSIX Bessel functions in favour of
    // _j[0,1,n]().  Where available on MSVC, use _j[0,1,n]() to avoid deprecated
    // function errors in client code (the specific warning is suppressed when
    // Ceres itself is built).
    inline double BesselJ0(double x) {
#if defined(CERES_MSVC_USE_UNDERSCORE_PREFIXED_BESSEL_FUNCTIONS)
        return _j0(x);
#else
        return j0(x);
#endif
    }
    inline double BesselJ1(double x) {
#if defined(CERES_MSVC_USE_UNDERSCORE_PREFIXED_BESSEL_FUNCTIONS)
        return _j1(x);
#else
        return j1(x);
#endif
    }
    inline double BesselJn(int n, double x) {
#if defined(CERES_MSVC_USE_UNDERSCORE_PREFIXED_BESSEL_FUNCTIONS)
        return _jn(n, x);
#else
        return jn(n, x);
#endif
    }

    // For the formulae of the derivatives of the Bessel functions see the book:
    // Olver, Lozier, Boisvert, Clark, NIST Handbook of Mathematical Functions,
    // Cambridge University Press 2010.
    //
    // Formulae are also available at http://dlmf.nist.gov

    // See formula http://dlmf.nist.gov/10.6#E3
    // j0(a + h) ~= j0(a) - j1(a) h
    template <typename T, int N> inline
        Jet<T, N> BesselJ0(const Jet<T, N>& f) {
        return Jet<T, N>(BesselJ0(f.a),
            -BesselJ1(f.a) * f.v);
    }

    // See formula http://dlmf.nist.gov/10.6#E1
    // j1(a + h) ~= j1(a) + 0.5 ( j0(a) - j2(a) ) h
    template <typename T, int N> inline
        Jet<T, N> BesselJ1(const Jet<T, N>& f) {
        return Jet<T, N>(BesselJ1(f.a),
            T(0.5) * (BesselJ0(f.a) - BesselJn(2, f.a)) * f.v);
    }

    // See formula http://dlmf.nist.gov/10.6#E1
    // j_n(a + h) ~= j_n(a) + 0.5 ( j_{n-1}(a) - j_{n+1}(a) ) h
    template <typename T, int N> inline
        Jet<T, N> BesselJn(int n, const Jet<T, N>& f) {
        return Jet<T, N>(BesselJn(n, f.a),
            T(0.5) * (BesselJn(n - 1, f.a) - BesselJn(n + 1, f.a)) * f.v);
    }

    // Jet Classification. It is not clear what the appropriate semantics are for
    // these classifications. This picks that std::isfinite and std::isnormal are "all"
    // operations, i.e. all elements of the jet must be finite for the jet itself
    // to be finite (or normal). For IsNaN and IsInfinite, the answer is less
    // clear. This takes a "any" approach for IsNaN and IsInfinite such that if any
    // part of a jet is nan or inf, then the entire jet is nan or inf. This leads
    // to strange situations like a jet can be both IsInfinite and IsNaN, but in
    // practice the "any" semantics are the most useful for e.g. checking that
    // derivatives are sane.

    // The jet is finite if all parts of the jet are finite.
    template <typename T, int N> inline
        bool isfinite(const Jet<T, N>& f) {
        if (!std::isfinite(f.a)) {
            return false;
        }
        for (int i = 0; i < N; ++i) {
            if (!std::isfinite(f.v[i])) {
                return false;
            }
        }
        return true;
    }

    // The jet is infinite if any part of the Jet is infinite.
    template <typename T, int N> inline
        bool isinf(const Jet<T, N>& f) {
        if (std::isinf(f.a)) {
            return true;
        }
        for (int i = 0; i < N; ++i) {
            if (std::isinf(f.v[i])) {
                return true;
            }
        }
        return false;
    }


    // The jet is NaN if any part of the jet is NaN.
    template <typename T, int N> inline
        bool isnan(const Jet<T, N>& f) {
        if (std::isnan(f.a)) {
            return true;
        }
        for (int i = 0; i < N; ++i) {
            if (std::isnan(f.v[i])) {
                return true;
            }
        }
        return false;
    }

    // The jet is normal if all parts of the jet are normal.
    template <typename T, int N> inline
        bool isnormal(const Jet<T, N>& f) {
        if (!std::isnormal(f.a)) {
            return false;
        }
        for (int i = 0; i < N; ++i) {
            if (!std::isnormal(f.v[i])) {
                return false;
            }
        }
        return true;
    }

    // Legacy functions from the pre-C++11 days.
    template <typename T, int N>
    inline bool IsFinite(const Jet<T, N>& f) {
        return isfinite(f);
    }

    template <typename T, int N>
    inline bool IsNaN(const Jet<T, N>& f) {
        return isnan(f);
    }

    template <typename T, int N>
    inline bool IsNormal(const Jet<T, N>& f) {
        return isnormal(f);
    }

    // The jet is infinite if any part of the jet is infinite.
    template <typename T, int N> inline
        bool IsInfinite(const Jet<T, N>& f) {
        return isinf(f);
    }

    // atan2(b + db, a + da) ~= atan2(b, a) + (- b da + a db) / (a^2 + b^2)
    //
    // In words: the rate of change of theta is 1/r times the rate of
    // change of (x, y) in the positive angular direction.
    template <typename T, int N> inline
        Jet<T, N> atan2(const Jet<T, N>& g, const Jet<T, N>& f) {
        // Note order of arguments:
        //
        //   f = a + da
        //   g = b + db

        T const tmp = T(1.0) / (f.a * f.a + g.a * g.a);
        return Jet<T, N>(atan2(g.a, f.a), tmp * (-g.a * f.v + f.a * g.v));
    }


    // pow -- base is a differentiable function, exponent is a constant.
    // (a+da)^p ~= a^p + p*a^(p-1) da
    template <typename T, int N> inline
        Jet<T, N> pow(const Jet<T, N>& f, double g) {
        T const tmp = g * pow(f.a, g - T(1.0));
        return Jet<T, N>(pow(f.a, g), tmp * f.v);
    }

    // pow -- base is a constant, exponent is a differentiable function.
    // We have various special cases, see the comment for pow(Jet, Jet) for
    // analysis:
    //
    // 1. For f > 0 we have: (f)^(g + dg) ~= f^g + f^g log(f) dg
    //
    // 2. For f == 0 and g > 0 we have: (f)^(g + dg) ~= f^g
    //
    // 3. For f < 0 and integer g we have: (f)^(g + dg) ~= f^g but if dg
    // != 0, the derivatives are not defined and we return NaN.

    template <typename T, int N> inline
        Jet<T, N> pow(double f, const Jet<T, N>& g) {
        if (f == 0 && g.a > 0) {
            // Handle case 2.
            return Jet<T, N>(T(0.0));
        }
        if (f < 0 && g.a == floor(g.a)) {
            // Handle case 3.
            Jet<T, N> ret(pow(f, g.a));
            for (int i = 0; i < N; i++) {
                if (g.v[i] != T(0.0)) {
                    // Return a NaN when g.v != 0.
                    ret.v[i] = std::numeric_limits<T>::quiet_NaN();
                }
            }
            return ret;
        }
        // Handle case 1.
        T const tmp = pow(f, g.a);
        return Jet<T, N>(tmp, log(f) * tmp * g.v);
    }

    // pow -- both base and exponent are differentiable functions. This has a
    // variety of special cases that require careful handling.
    //
    // 1. For f > 0:
    //    (f + df)^(g + dg) ~= f^g + f^(g - 1) * (g * df + f * log(f) * dg)
    //    The numerical evaluation of f * log(f) for f > 0 is well behaved, even for
    //    extremely small values (e.g. 1e-99).
    //
    // 2. For f == 0 and g > 1: (f + df)^(g + dg) ~= 0
    //    This cases is needed because log(0) can not be evaluated in the f > 0
    //    expression. However the function f*log(f) is well behaved around f == 0
    //    and its limit as f-->0 is zero.
    //
    // 3. For f == 0 and g == 1: (f + df)^(g + dg) ~= 0 + df
    //
    // 4. For f == 0 and 0 < g < 1: The value is finite but the derivatives are not.
    //
    // 5. For f == 0 and g < 0: The value and derivatives of f^g are not finite.
    //
    // 6. For f == 0 and g == 0: The C standard incorrectly defines 0^0 to be 1
    //    "because there are applications that can exploit this definition". We
    //    (arbitrarily) decree that derivatives here will be nonfinite, since that
    //    is consistent with the behavior for f == 0, g < 0 and 0 < g < 1.
    //    Practically any definition could have been justified because mathematical
    //    consistency has been lost at this point.
    //
    // 7. For f < 0, g integer, dg == 0: (f + df)^(g + dg) ~= f^g + g * f^(g - 1) df
    //    This is equivalent to the case where f is a differentiable function and g
    //    is a constant (to first order).
    //
    // 8. For f < 0, g integer, dg != 0: The value is finite but the derivatives are
    //    not, because any change in the value of g moves us away from the point
    //    with a real-valued answer into the region with complex-valued answers.
    //
    // 9. For f < 0, g noninteger: The value and derivatives of f^g are not finite.

    template <typename T, int N> inline
        Jet<T, N> pow(const Jet<T, N>& f, const Jet<T, N>& g) {
        if (f.a == 0 && g.a >= 1) {
            // Handle cases 2 and 3.
            if (g.a > 1) {
                return Jet<T, N>(T(0.0));
            }
            return f;
        }
        if (f.a < 0 && g.a == floor(g.a)) {
            // Handle cases 7 and 8.
            T const tmp = g.a * pow(f.a, g.a - T(1.0));
            Jet<T, N> ret(pow(f.a, g.a), tmp * f.v);
            for (int i = 0; i < N; i++) {
                if (g.v[i] != T(0.0)) {
                    // Return a NaN when g.v != 0.
                    ret.v[i] = std::numeric_limits<T>::quiet_NaN();
                }
            }
            return ret;
        }
        // Handle the remaining cases. For cases 4,5,6,9 we allow the log() function
        // to generate -HUGE_VAL or NaN, since those cases result in a nonfinite
        // derivative.
        T const tmp1 = pow(f.a, g.a);
        T const tmp2 = g.a * pow(f.a, g.a - T(1.0));
        T const tmp3 = tmp1 * log(f.a);
        return Jet<T, N>(tmp1, tmp2 * f.v + tmp3 * g.v);
    }

    // Note: This has to be in the ceres namespace for argument dependent lookup to
    // function correctly. Otherwise statements like CHECK_LE(x, 2.0) fail with
    // strange compile errors.
    template <typename T, int N>
    inline std::ostream &operator<<(std::ostream &s, const Jet<T, N>& z) {
        s << "[" << z.a << " ; ";
        for (int i = 0; i < N; ++i) {
            s << z.v[i];
            if (i != N - 1) {
                s << ", ";
            }
        }
        s << "]";
        return s;
    }

}  // namespace ceres

namespace Eigen {

    // Creating a specialization of NumTraits enables placing Jet objects inside
    // Eigen arrays, getting all the goodness of Eigen combined with autodiff.
    template<typename T, int N>
    struct NumTraits<ceres::Jet<T, N>> {
        typedef ceres::Jet<T, N> Real;
        typedef ceres::Jet<T, N> NonInteger;
        typedef ceres::Jet<T, N> Nested;
        typedef ceres::Jet<T, N> Literal;

        static typename ceres::Jet<T, N> dummy_precision() {
            return ceres::Jet<T, N>(1e-12);
        }

        static inline Real epsilon() {
            return Real(std::numeric_limits<T>::epsilon());
        }

        static inline int digits10() { return NumTraits<T>::digits10(); }

        enum {
            IsComplex = 0,
            IsInteger = 0,
            IsSigned,
            ReadCost = 1,
            AddCost = 1,
            // For Jet types, multiplication is more expensive than addition.
            MulCost = 3,
            HasFloatingPoint = 1,
            RequireInitialization = 1
        };

        template<bool Vectorized>
        struct Div {
            enum {
#if defined(EIGEN_VECTORIZE_AVX)
                AVX = true,
#else
                AVX = false,
#endif

                // Assuming that for Jets, division is as expensive as
                // multiplication.
                Cost = 3
            };
        };

        static inline Real highest() { return Real(std::numeric_limits<T>::max()); }
        static inline Real lowest() { return Real(-std::numeric_limits<T>::max()); }
    };

#if EIGEN_VERSION_AT_LEAST(3, 3, 0)
    // Specifying the return type of binary operations between Jets and scalar types
    // allows you to perform matrix/array operations with Eigen matrices and arrays
    // such as addition, subtraction, multiplication, and division where one Eigen
    // matrix/array is of type Jet and the other is a scalar type. This improves
    // performance by using the optimized scalar-to-Jet binary operations but
    // is only available on Eigen versions >= 3.3
    template <typename BinaryOp, typename T, int N>
    struct ScalarBinaryOpTraits<ceres::Jet<T, N>, T, BinaryOp> {
        typedef ceres::Jet<T, N> ReturnType;
    };
    template <typename BinaryOp, typename T, int N>
    struct ScalarBinaryOpTraits<T, ceres::Jet<T, N>, BinaryOp> {
        typedef ceres::Jet<T, N> ReturnType;
    };
#endif  // EIGEN_VERSION_AT_LEAST(3, 3, 0)

}  // namespace Eigen

#endif  // CERES_PUBLIC_JET_H_