

矩阵,网格,每个元素之间有关联,如连接,相通。。。均可用黑白染色来分类
比如此题,每个格子与另外的已知数格子有关系,但是无法在图中之间得知是哪几个人,所以无法确定其他人而推出小明的关系人数。。。因此,我们考虑整体。。。
此题中,并不是要去遍历黑白染色,而是由这样一种思想,我们可以这样处理所有人。设w[i]为每一个人的关系数之和,因为关系是双向的,a与b有关系,w[a]++,则b与a也有关系,w[b]++;所以,黑人的关系和等于白人的关系和。所以,除了小明的关系+除了小明以外的人的关系=总关系和
黑白染色法:(DFS,BFS?)从a1遍历,,设a1为白色,若ai与a1有关系,则ai为黑色,若无关系,则不作处理。另外,若两人有关系,但是已经被染成同色(出现了奇环),则立即可判定不能成为二分图。直到把所有关系遍历完,我们得到一个二分图,黑白两个阵营
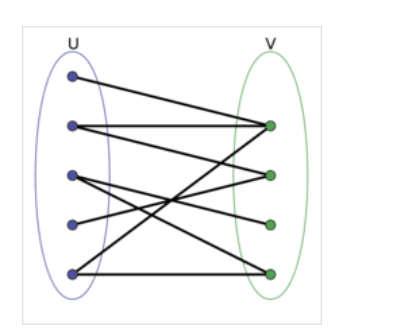
偶数环:一个环,边的数量为偶数.....二分图没有回路。。所有的环都是奇数环.