Tarjan缩点学习笔记

前置知识

强连通分量，就是图上的环

用途

(Tarjan) 缩点就是在图上找强连通分量的算法。

思想

用 (dfs) 去搜索一个图，不搜搜过的节点，首先搜出来的是一棵树，然后这棵树肯定不会有横叉边，因为如果有横叉边的就可以继续沿横叉边搜下去。所以这样搜出来的树肯定只有返祖边，只要有返祖边就会有一个强连通分量（就是一个环）。 (Tarjan) 缩点算法就是通过在 (dfs) 的时候通过打时间戳来找返祖边，进而找到强连通分量的。

因为如果有返祖边，那么可以到达的时间最小的点肯定小于当前点的时间戳，所以我们就可以通过打时间戳来找返祖边。

算法流程

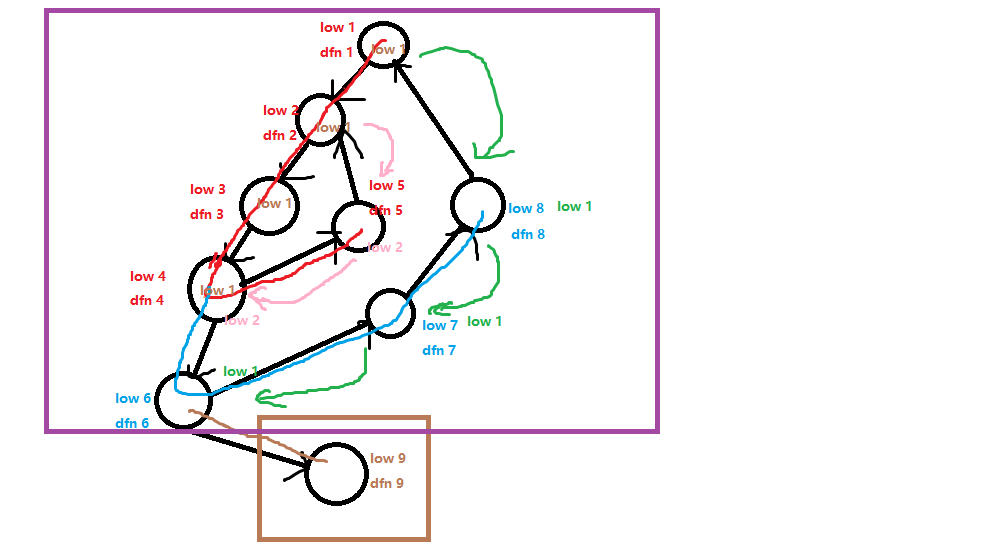
如图

1. 红色代表第一次找到第一个返祖边的过程
2. 粉红色代表回溯并更新 (low) 数组的过程
3. 蓝色代表再次找另一个返祖边的过程（因为 (dfs) 搜到底的特性，所以不会缩点，会继续搜下去）
4. 绿色代表再次回溯更新 (low) 数组的过程
5. 棕色代表再次寻找返祖边
6. 没有找到，对棕色部分进行缩点
7. 然后一直回溯到 (low=dfn=1) ，对紫色部分进行缩点

寻找操作和回溯更新操作

	if (!dfn[ed[i].e])
	{
		Tarjan(ed[i].e);
		low[x]=min(low[x],low[ed[i].e]);
	}

找的返祖边更新low的操作

	else if (mark[ed[i].e])
	low[x]=min(low[x],dfn[ed[i].e]);

缩点操作

	if (low[x]==dfn[x])
	{
		int k;
		++sum;
		do {
			k=st.top();
			st.pop();
			mark[k]=0;
			pointsz[sum]++;
			color[k]=sum;
		} while (k!=x);
	}

因为 (low[x]==dfn[x]) 所以已经到达了当前栈顶到现在的点所能到达的深度最浅的祖先，证明如果再往上回溯当前强连通分量里的点将无法到达，把到这个点以前栈里所有点染同一种颜色，表示在同一个强联通分量里。

因为要把当前的点也从栈里弹出来，所以要用 (do) (while) 的循环形式，先弹再判断。

(Q:) 为什么要用 (mark) 数组单独标记在不在栈里面呢？？

(A:) 例子：如图当一个正在缩点的点指向一个已经缩完的点集时，如果没有 (mark) 数组单独标记，就会把 (low) 的值更新为一个在回溯时永远也到不了的值，完成不了这个点所在点集的缩点。

例题

P2863 牛的舞会

题目链接

就是找大于 (1) 的强连通分量的个数。

#include<bits/stdc++.h>
#include<stack>
using std::min;
using std::stack;
const int N=1e4+100,M=5e4+100;
struct edge{
	int s,e,net;
}ed[M];
stack<int>st;
int n,m,tot,sum,idx;
int head[N],dfn[N],color[N],low[N],pointsz[N];
bool mark[N];
inline void Tarjan(int x)
{
	st.push(x);
	mark[x]=1;
	dfn[x]=low[x]=++idx;
	for (int i=head[x];i;i=ed[i].net)
	if (!dfn[ed[i].e])
	{
		Tarjan(ed[i].e);
		low[x]=min(low[x],low[ed[i].e]);
	}
	else if (mark[ed[i].e]) low[x]=min(low[x],dfn[ed[i].e]);
	if (low[x]==dfn[x])
	{
		int k;
		++sum;
		do {
			k=st.top();
			st.pop();
			mark[k]=0;
			pointsz[sum]++;
			color[k]=sum;
		} while (k!=x);
	}
	return ;
}
inline void add(int s,int e)
{
	ed[++tot]=(edge){s,e,head[s]};
	head[s]=tot;
	return ;
}
int main()
{
	scanf("%d%d",&n,&m);
	for (int i=1;i<=m;i++)
	{
		int s,e;
		scanf("%d%d",&s,&e);
		add(s,e);
	}
	for (int i=1;i<=n;i++)
	if (!dfn[i]) Tarjan(i);
	int ans=0;
	for (int i=1;i<=sum;i++)
	if (pointsz[i]>1) ans++;
	printf("%d
",ans);
	return 0;
}

P2341 [HAOI2006]受欢迎的牛

题目链接

#include<iostream>
#include<cstdio>
#include<stack>
using namespace std;
const int N=1e4+5,M=5e4+1;
int n,m,tot,idx,sum;
stack<int>s;
int head[N],color[N],dfn[N],dnum[N],start[N],low[N];
bool mark[N];
struct edge{
    int s,e,next;
}ed[M];
void tarjan(int x)
{
	low[x]=dfn[x]=++idx;
	s.push(x);
	mark[x]=1;
	for (int i=head[x];i;i=ed[i].next)
	if (!dfn[ed[i].e])
	{
		tarjan(ed[i].e);
		low[x]=min(low[ed[i].e],low[x]);
	}
	else if (mark[ed[i].e])
	low[x]=min(low[x],dfn[ed[i].e]);
	if (low[x]==dfn[x])
	{
		++sum;
		int k;
		do
		{
			k=s.top();
			s.pop();
			mark[k]=0;
			color[k]=sum;
			dnum[sum]++;
		}while (k!=x);
	}
	return ;
}
inline void add(int s,int e)
{
	ed[++tot]=(edge){s,e,head[s]};
	head[s]=tot;
	return ;
}
int main()
{
    scanf("%d%d",&n,&m);
    int s,e;
    for (int i=1;i<=m;i++)
    {
        scanf("%d%d",&s,&e);
        add(s,e);
    }
    for (int i=1;i<=n;i++)
    if (!dfn[i]) tarjan(i);
    for (int i=1;i<=tot;i++)
    if (color[ed[i].s]!=color[ed[i].e])
    start[color[ed[i].s]]++;
    int num=0,ans;
    for (int i=1;i<=sum;i++)
    {
    	if (!start[i])
    	{
    		num++;
    		ans=i;
		}
		if (num>=2)
		{
			printf("0
");
			return 0;
		}
	}
	printf("%d",dnum[ans]);
    return 0;
}

参考资料

Tarjan缩点详解