洛谷P1044 栈
题目背景
栈是计算机中经典的数据结构，简单的说，栈就是限制在一端进行插入删除操作的线性表。
栈有两种最重要的操作，即 pop（从栈顶弹出一个元素）和 push（将一个元素进栈）。
栈的重要性不言自明，任何一门数据结构的课程都会介绍栈。宁宁同学在复习栈的基本概念时，想到了一个书上没有讲过的问题，而他自己无法给出答案，所以需要你的帮忙。
题目描述
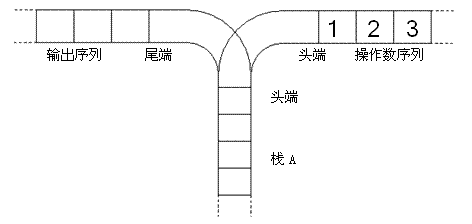
宁宁考虑的是这样一个问题：一个操作数序列，1,2,ldots ,n1,2,…,n（图示为 1 到 3 的情况），栈 A 的深度大于 nn。
现在可以进行两种操作，
- 将一个数，从操作数序列的头端移到栈的头端（对应数据结构栈的 push 操作）
- 将一个数，从栈的头端移到输出序列的尾端（对应数据结构栈的 pop 操作）
使用这两种操作，由一个操作数序列就可以得到一系列的输出序列，下图所示为由 1 2 3 生成序列 2 3 1 的过程。
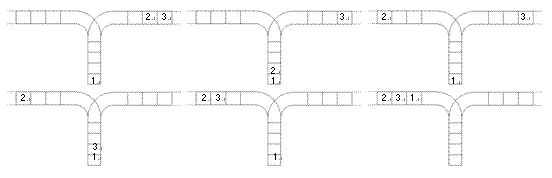
（原始状态如上图所示）
你的程序将对给定的 nn，计算并输出由操作数序列 1,2,ldots,n1,2,…,n 经过操作可能得到的输出序列的总数。
输入格式
输入文件只含一个整数 nn（1 leq n leq 181≤n≤18）。
输出格式
输出文件只有一行，即可能输出序列的总数目。
对于上面这个解决方法的解释：x是最后一个出栈的，可以把整个过程分为三个子过程。
1）
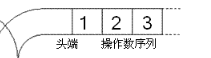开始时，数字按从小到大排列，准备进栈。
2）1~x-1 完成进栈出栈 ，栈空
3）x进栈
4）x+1~n完成进栈出栈 ，栈空
洛谷P1722 矩阵II
题目背景
usqwedf 改编系列题。
题目描述
如果你在百忙之中抽空看题，请自动跳到第六行。
众所周知，在中国古代算筹中，红为正，黑为负……
给定一个1*(2n)的矩阵（usqwedf：这不是一个2n的队列么），现让你自由地放入红色算筹和黑色算筹，使矩阵平衡[即对于所有的i(1<=i<=2n)，使第1~i格中红色算筹个数大于等于黑色算筹]
问有多少种方案满足矩阵平衡。
见样例解释。
输入格式
正整数 n
输出格式
方案数t对100取模
本题就是卡特兰数的经典问题。本题和上题本质上是等价的。因为红色可以看作入栈，黑色可以看成出栈。 上题中任何一种输出序列都一一对应着本题的一种排列方式。因为入栈-出栈=栈中的元素数，因为栈中的元素数>=0，所以入栈>=出栈。所以本题可以类比为上题。这个类比的巧妙之处在于把实体“棋子”类比为一个入栈和出栈的过程。