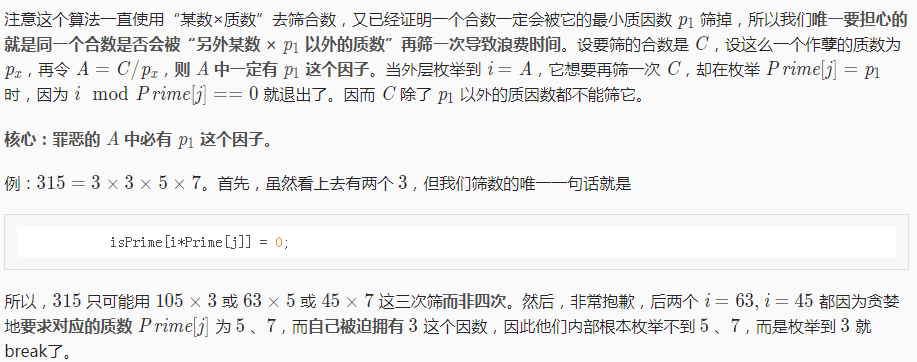
#include <cstdio> #include <cstring> bool isPrime[100000010]; //isPrime[i] == 1表示:i是素数 int Prime[5000010], cnt = 0; //Prime存质数 void GetPrime(int n)//筛到n { memset(isPrime, 1, sizeof(isPrime)); //以“每个数都是素数”为初始状态,逐个删去 isPrime[1] = 0;//1不是素数 for(int i = 2; i <= n; i++) { if(isPrime[i])//没筛掉 Prime[++cnt] = i; //i成为下一个素数 for(int j = 1; j <= cnt && i*Prime[j] <= n/*不超上限*/; j++) { //从Prime[1],即最小质数2开始,逐个枚举已知的质数,并期望Prime[j]是(i*Prime[j])的最小质因数 //当然,i肯定比Prime[j]大,因为Prime[j]是在i之前得出的 isPrime[i*Prime[j]] = 0; if(i % Prime[j] == 0)//i中也含有Prime[j]这个因子 break; //重要步骤。见原理 } } } int main() { int n, q; scanf("%d %d", &n, &q); GetPrime(n); while (q--) { int k; scanf("%d", &k); printf("%d ", Prime[k]); } return 0; }
原理概述
代码中,外层枚举 i=1→n。对于一个 i,经过前面的腥风血雨,如果它还没有被筛掉,就加到质数数组 Prime[]中。下一步,是用 i 来筛掉一波数。
内层从小到大枚举 Prime[j]。i×Prime[j]i 是尝试筛掉的某个合数,其中,我们期望 Prime[j]P是这个合数的最小质因数 (这是线性复杂度的条件,下面叫做“筛条件”)。它是怎么得到保证的?
jj 的循环中,有一句就做到了这一点:
if(i % Prime[j] == 0)
break; jj 循环到 i mod Prime[j] == 0就恰好需要停止的理由是:

小提示:
当 ii 还不大的时候,可能会一层内就筛去大量合数,看上去耗时比较大,但是由于保证了筛去的合数日后将不会再被筛(总共只筛一次),复杂度是线性的。到 ii 接近 nn 时,每层几乎都不用做什么事。
建议看下面两个并不复杂的证明,你能更加信任这个筛法,利于以后的扩展学习。
正确性(所有合数都会被标记)证明

线性复杂度证明