带通/带阻滤波
顾名思义,圆环带通过或不通过。
1.理想的带通/带阻滤波
理想带阻滤波函数为:
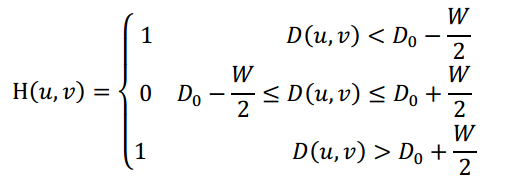
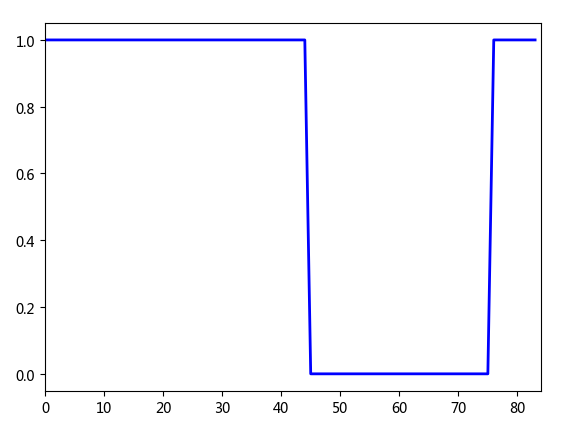
W为带宽。理想的带通滤波器与此相反,1减去带阻即可得到。



部分代码:

# 定义函数,理想的带阻/通滤波模板 def IdealBand(src, w, d0, ftype): template = np.zeros(src.shape, dtype=np.float32) # 构建滤波器 r, c = src.shape for i in np.arange(r): for j in np.arange(c): distance = np.sqrt((i - r / 2) ** 2 + (j - c / 2) ** 2) if (d0-w/2) <= distance <= (d0+w/2): template[i, j] = 0 else: template[i, j] = 1 if ftype == 'pass': template = 1 - template return template
2.Butterworth 带通/带阻滤波
n阶Butterworth带阻函数为:
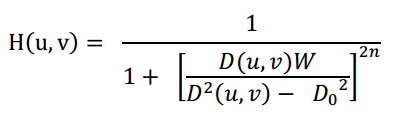
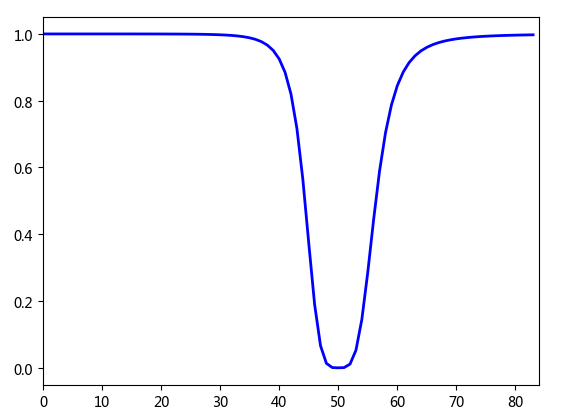
带通函数与此相反,1减带阻即可。



部分代码:

# 定义函数,巴特沃斯带阻/通滤波模板 def ButterworthBand(src, w, d0, n, ftype): template = np.zeros(src.shape, dtype=np.float32) # 构建滤波器 r, c = src.shape for i in np.arange(r): for j in np.arange(c): distance = np.sqrt((i - r / 2) ** 2 + (j - c / 2) ** 2) template[i, j] = 1/(1+(distance*w/(distance**2 - d0**2))**(2*n)) if ftype == 'pass': template = 1 - template return template
3.Gaussian带通/带阻滤波
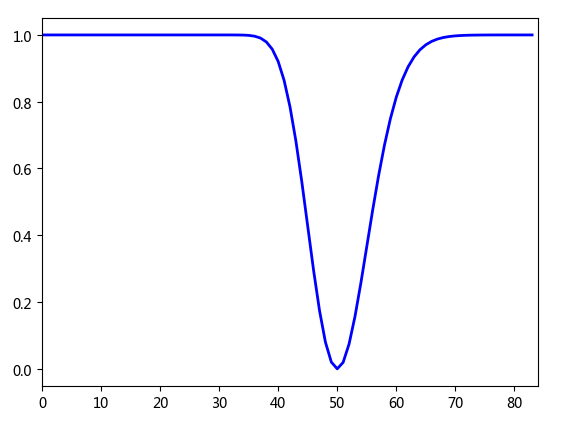
高斯带阻滤波函数为:
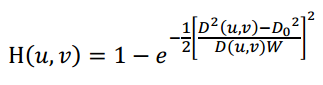
带通滤波函数与此相反,1减带阻即可。



部分代码:

# 定义函数,高斯带阻/通滤波模板 def GaussianBand(src, w, d0, ftype): template = np.zeros(src.shape, dtype=np.float32) # 构建滤波器 r, c = src.shape for i in np.arange(r): for j in np.arange(c): distance = np.sqrt((i - r / 2) ** 2 + (j - c / 2) ** 2) temp = ((distance**2 - d0**2)/(distance*w+0.00000001))**2 template[i, j] = 1 - np.exp(-0.5 * temp) if ftype == 'pass': template = 1 - template return template
