一、堆和二叉堆
堆,英文名称Heap,所谓二叉堆(也有直接称二叉堆为堆的),本质上是一个完全二叉树,前面也提到过,如果树接近于完全二叉树或者满二叉树,采用顺序存储代价会小一点,因此常见的二叉堆均是顺序实现的。
按照排列的顺序可以分为最大堆和最小堆,最大堆的特征是父节点一定大于(依据情况判断是大于等于还是严格大于,数据结构归根到底还是用来使用的)子节点的数据。同样,有最大堆就会有最小堆,最小堆的 父节点数据小于其子节点的数据,因此根节点的数据是最小的。下面左图是一个最小堆,右图是一个最大堆。
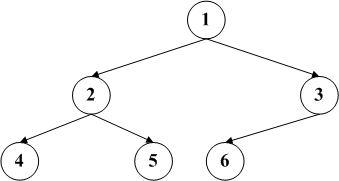
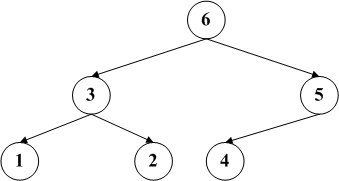
二、二叉堆的插入和删除
详细来看,二叉堆的主要操作就是插入和删除。以一个最小堆为例,我们详细介绍插入和删除的操作。
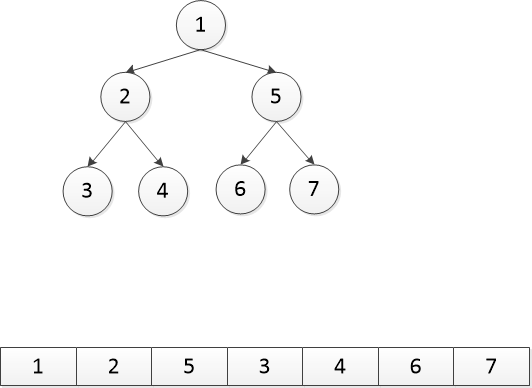
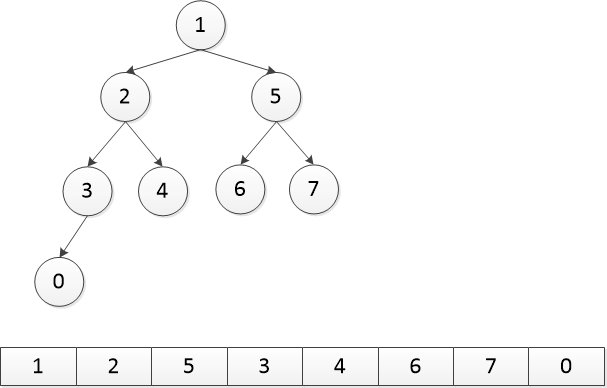
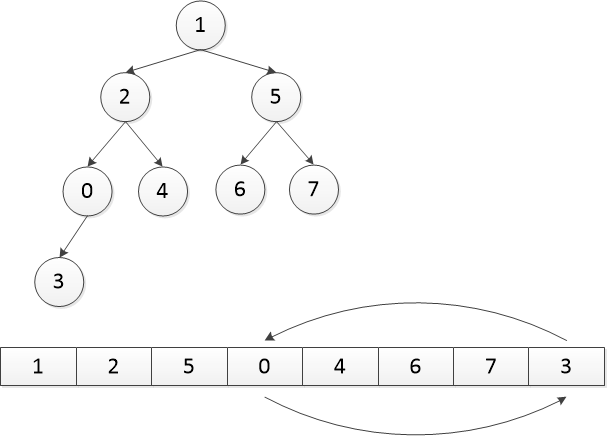

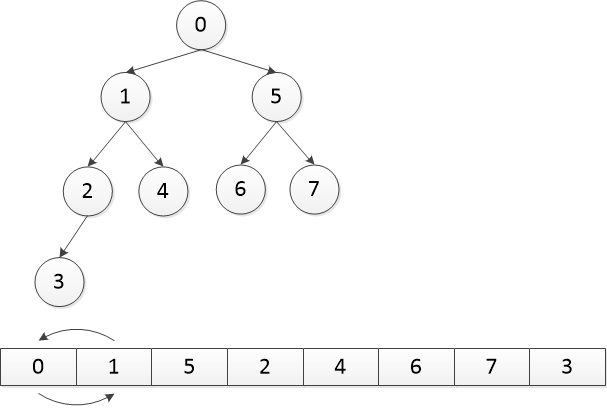
以上是一个最小二叉堆的插入过程,比如我们要插入一个节点0,但是他的数据小于它父节点的数据,因此它和它父节点交换数据,如上面的第三张图所示。然后继续判断,它仍连续两次小于父节点数据,因此再交换两次数据,形成最终的那张图,就是插入后的最小二叉堆。

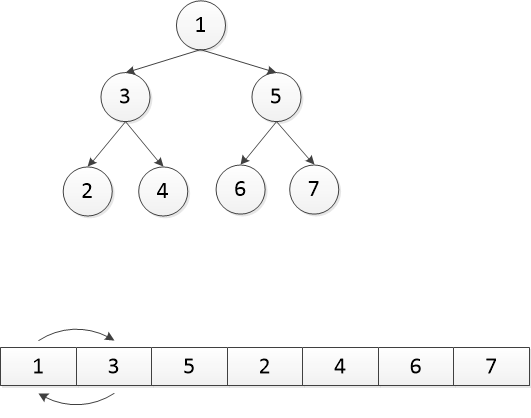
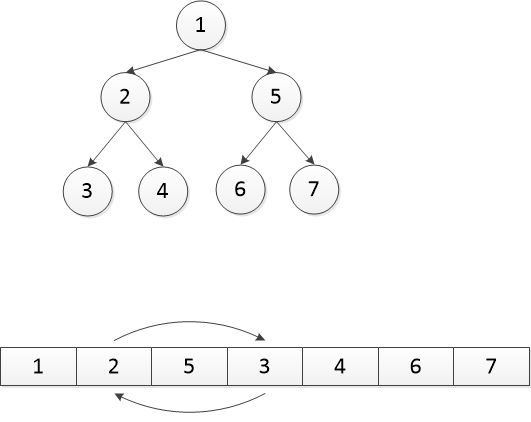
一般来说,二叉堆的删除主要是指删除堆顶的数据,即根节点的数据。我们使用之前插入后得到的二叉堆作为目标,我们对其进行删除操作,假设再次删除节点0,然后将数组中最后一位(节点3)填充进去;然后和子节点的数据进行比较,这时候我们必须要从左右子节点中选出更小的那一个作比较,显然是左节点1较小;如果该节点数据大于子节点(较小的那个)的数据,那就和子节点数据进行交换,直至符合条件;
而查找性的删除则比较复杂,从堆尾补充进删除位置的新数据首先要和父节点的数据进行比较,如果小于,就把该节点一直往上交换,直至停止。但本实例中该节点是根节点,不存在父节点,因此就没有这一步;然后按照上面那一段描述与子节点进行比较,交换。
三、二叉堆的Java实现
成员域由ArrayList<Y> data代表堆中的数据,因为数组无法适配泛型。
插入
public void insert(Y y) { data.add(y); int index = data.size() - 1; while(((index + 1) / 2 - 1) >= 0 && data.get(index).compareTo(data.get((index + 1) / 2 - 1)) < 0) { Y temp = data.get((index + 1) / 2 - 1); data.set((index + 1) / 2 - 1, y); data.set(index,temp); index = (index + 1) / 2 - 1; } }
删除
public boolean delete(Y y) { if(data.size() == 0) return false; else if (data.indexOf(y) == -1) return false; else { int index = data.indexOf(y); data.set(index, data.get(data.size() - 1)); data.remove(data.size() - 1);
/* parent */
while(((index + 1) / 2 - 1) >= 0 && data.get(index).compareTo(data.get((index + 1) / 2 - 1)) < 0) { Y temp = data.get((index + 1) / 2 - 1); data.set((index + 1) / 2 - 1, data.get(index)); data.set(index,temp); index = (index + 1) / 2 - 1; } /* child */ while((2 * index + 1) <= data.size()-1) { if ((2 * index + 2) <= data.size()-1) //如果该节点左右子树均存在 { int cmp = data.get(2 * index + 1).compareTo(data.get(2 * index + 2)); //比较子树的大小 if (cmp > 0) //左子树大于右子树,则交换右子树 { if (data.get(index * 2 + 2) .compareTo(data.get(index)) < 0 ) { Y temp = data.get(index * 2 + 2); data.set(index * 2 + 2, data.get(index)); data.set(index, temp); index = index * 2 + 2; }
else
break; } else //右子树大于左子树,则交换左子树 { if(data.get(index * 2 + 1) .compareTo(data.get(index)) < 0 ) { Y temp = data.get(index * 2 + 1); data.set(index * 2 + 1, data.get(index)); data.set(index, temp); index = index * 2 + 1; }
else
break; } } else if ((2 * index + 2) > data.size()-1) //只存在左子树 { if(data.get(index * 2 + 1) .compareTo(data.get(index)) < 0 ) { //判断左子树和节点大小 Y temp = data.get(index * 2 + 1); data.set(index * 2 + 1, data.get(index)); data.set(index, temp); index = index * 2 + 1; }
else
break; } } return true; } }
测试代码1

以此堆为例,插入0后删除0

Heap <Integer> h = new Heap<>(); Integer [] i = {1,2,5,3,4,6,7}; for (int j = 0; j < i.length; j++) { h.insert(i[j]); } h.traverse(); System.out.println(); h.insert(0); h.traverse(); System.out.println(); h.delete(0); h.traverse();
结果1:
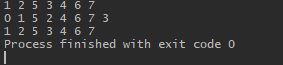
————————————————————————————————————————————————————————
测试代码2


Heap <Integer> h = new Heap<>(); Integer [] i = {10,20,40,30,60,80,110,50,70,90,100}; for (int j = 0; j < i.length; j++) { h.insert(i[j]); } h.traverse(); System.out.println(); h.insert(0); h.traverse(); System.out.println(); h.delete(0); h.traverse();
结果2:

