是真懂还是假懂？
Floyed算法：是最短路径算法可以说是最慢的一个。
原理：O（n^3）的for循环，对每一个中间节点k做松弛（寻找更短路径）；
但它适合算多源最短路径，即任意两点间的距离。
但spfa，迪杰斯特拉就只能算一个点到其他任一点的最短路径。
关键在于，我们真的真正理解floyed吗？
就是因为它太短了，以至于我们有些人（神仙除外）看代码后看到这样一个语句：
d[i][j]=min(d[i][j],d[i][k]+d[k][j])
也就是说，对于每一个中转点k来说，进行O（n^2）的松弛，一定能找到最短路径。
虽不是最优，但是松弛次数来凑！
这大概就是我们（之前的我）的无须证明的，想当然的理解，并背下来了它，以便以后想TLE时用。（？？？O（n^3））；
so？
Floyed本质是dp；
递推公式：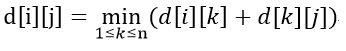
（图片源自网络大佬）
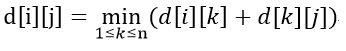（图片源自网络大佬）
众所周知，dp（动态规划）要满足无后效性。也就是说。。。。。。
还是先举个例子：
我们设k取某一个k1时满足k1为最终点i到j最短路经过的点，但是在外层循环到k1时d[i][k1]和d[k1][j]并没有取到最小值，因为k1只能取一次，那么往后再循环是不是就取不到k1了呢？？
答案当然不是的（不然这个算法为什么正确?）
还是那句话，dp无后效性，
也就是说，k不单单是枚举，还是一个状态变量，找i和j之间通过编号不超过k（k从1到n）的节点的最短路径（一定要注意，这里是当前最短路径，
k之前的已经变成最短路了,对于每一个k，我们都进行了n^2的充分枚举(ij)，已保证当前已经满足对从1到k的节点最优，
那么当k枚举完所有点，那么一定是最优的了
换句话说，在d[i][j]=min(d[i][j],d[i][k]+d[k][j])
公式中，因为k之前已经作为i或者j被枚举过了；,d[i][k]和d[k][j] 已经被1到k枚举过了
那么他们一定是1到k节点中最优的路径，等枚举到n时，所有的都枚举完了，那么它们就是
基本代码:
for(k=1;k<=n;k++) //中转节点 for(i=1;i<=n;i++) 第二层循环 for(j=1;j<=n;j++) 第三层循环 if(e[i][j]>e[i][k]+e[k][j] )如果直接到达比通过k这个中转接点到达的距离短 e[i][j]=e[i][k]+e[k][j];那么就更新松弛
算法复杂度O（n^3），这也是为什么平常很少使用的原因。
例题校内题目：
城市交通费
【问题描述】
有 n 个城市，编号 1~n。其中 i 号城市的繁华度为 pi。省内有 m 条可以双向同行的高速
公路，编号 1~m。编号为 j 的高速公路连接编号为 aj 和 bj 两个城市，经过高速公路的费用
是 wj。若从城市 x 出发到某城市 y，除了需要缴纳高速公路费用，还要缴纳“城市建设费”
（为从 x 城市到 y 城市所经过的所有城市中繁华度的最大值，包括 x 和 y 在内）。
现提出 q 个询问，每个询问给出一组 x 和 y，你需要回答从 x 出发到 y 城市，所需要的
最低交通费（高速公路费+城市建设费）是多少。
【输入】
第一行三个整数 n,m,q。
第二行 n 个整数，表示 p1~pn。
接下来 m 行中，每行 3 个正整数，第 j 行包含 Aj，Bj，Wj。
随后 Q 行每组两个正整数 x，y 表示一组询问。
【输出】
共 Q 行，为对 Q 个问题的回答：x 城市到 y 城市的最小交通费用。
【样例输入】
5 7 2
2 5 3 3 4
1 2 3
1 3 2
2 5 3
5 3 1
5 4 1
2 4 3
3 4 4
1 4
2 3
【样例输出】
8
9
【数据范围及约定】
n≤250，m≤20000，Q≤10000，Pi≤10000，Wj≤2000，保证任意两个城市可以互相到达。
【样例说明】
图中，代表城市的格子中第一个数字是城市编号，第二个红色数字是该城市的繁华度。
（1）从城市 1 到城市 4 的最小交通费用路线是：1 3 5 4；公路费是 2+1+1=4；城市建设费是
max{2,3,4,3}=4；总交通费用 4+4=8。
（2）从城市 2 到城市 3 的最小交通费用路线是：2 5 3；公路费是 3+1=4；城市建设费是
max{5,4,3}=5；总交通费用 4+5=9。
这个题看起来就是一个最短路问题。
问题是Q（询问次数）的范围到了一万，一万次询问，不管是spfa还是堆优化迪杰斯特拉，都得爆炸。
那么，我们平时鸟都不鸟的Floyed就排上了用场；
但题目中给的点数为250，三次方为15625000，不会爆TLE，
可以使用，对于一万次询问，O（1）询问就可以过了。
但是，这个题目有一个附加条件：繁华度。
怎样在floyed算法中加入繁华度来考虑呢？
代码：（注意floyed部分）
#include<iostream> #include<cstring> #include<cstdio> #include<queue> #include<algorithm> using namespace std; int n,m,q,p[300],aj,bj,wj,x,y,f[300][300],a[300][300],top,t[300]; int cmp(int x,int y) { return p[x]<p[y]; } int main() { memset(a,63,sizeof(a)); top=0; scanf("%d%d%d",&n,&m,&q); for(int i=1;i<=n;i++)//正常输入 scanf("%d",&p[i]); for(int i=1;i<=m;i++) { scanf("%d%d%d",&aj,&bj,&wj); a[aj][bj]=min(a[aj][bj],wj);//初始化 a[bj][aj]=min(a[bj][aj],wj);//这是邻接矩阵类型的，没用链式前向星 } for(int i=1;i<=n;i++) { a[i][i]=0;//对角线置为0 t[i]=i;//编号 } sort(t+1,t+1+n,cmp);//t数组开始时是编号，但经过sort排序后就变成了城市繁华度从小到大的顺序 for(int i=1;i<=n;i++) for(int j=1;j<=n;j++) f[i][j]=a[i][j]+max(p[i],p[j]);//f数组即为答案数组，这里初始化 for(int k=1;k<=n;k++) for(int i=1;i<=n;i++) for(int j=1;j<=n;j++) { a[i][j]=min(a[i][j],a[i][t[k]]+a[t[k]][j]);//a数组就是最短路数组 f[i][j]=min(f[i][j],a[i][j]+max(p[i],max(p[j],p[t[k]])));
f数组就是答案数组，a数组不受f数组影响，有可能a更新了，但是f将最大繁华值考虑进去后并没有更新，那么a数组保留最短路为以后的更新做铺垫
} for(int i=1;i<=q;i++) { scanf("%d%d",&x,&y); printf("%d ",f[x][y]); } return 0; }
完结撒花。