开始瞎扯:
LCS:最长公共子序列
LIS:最长上升子序列
LCIS:最长公共上升子序列
以及许许多多同类的搞不清的东西。。。。。。
LIS:
最长上升子序列。
例如:
1 5 3 6 3 3 6 2中
能够组成的最长上升子序列长度为5(1 3 3 3 6)。
1 7 3 5 9 4 8中最长上升子序列长度为4(1 3 4 8,1 3 5 8,1 3 5 9.。。。)
有可能很多。
重点来了(敲!)如何求呢?
动态规划DP:
动态规划一般可分为线性动规,区域动规,树形动规,背包动规四类。
可以用动态规划求解的问题要满足无后效性原则,也就是你可以整段问题划分成子阶段,或者子状态,每一个状态都可以满足由之前的状态推得,并且之前的状态在已经确定最优解的情况下在后面的状态或者新的元素被考虑到时没有任何影响,那么这个题就可以用动态规划求解。
我们对LIS进行分析,很容易发现:
我们从第一个元素往后推,很明显前面最长子序列不会对后面的答案造成影响。
那么考虑用动态规划来做:
思路及推导:
从0开始想思路:
现在数列中只有1个元素:2,那么自然的,LIS长度为1。
加入1个元素,接着可以想,这个元素会对结果造成什么影响呢?
如果这个元素大于等于2的话,很明显最长上升子序列的长度就变为2了。
如果这个比2小,那么最长上升子序列长度还是1,只不过变成了两个了。
我们设加入的元素为0(比2小)放在序列里。
2个元素还是不能体现出规律来,我们继续:
设再加入个1:,那么序列变成2 0 1。
人眼观察,可以得知最长上升子序列变成了2。
为什么会这样呢?
1比0大,而0在1之前序列中,我们我们可以考虑“接上”以0为末尾数的最长子序列,然后加入当前的这个数,使序列的长度+1。以0为末尾数的最长子序列很明显是在满足上升这一条件的情况下到当前元素最长的子序列。
于是我们按照思路来设:dp[i]表示以第i个数为结尾的,最长上升子序列的长度。
要找到当前元素前面的序列中最长的子序列,只需要在之前的,满足结尾元素小于当前元素的,dp数组中寻找一个maxdp值。
找到后,我们把当前这个数接上去(++)。
如果前面的数都不如当前数小,那么这个数只能从自己开始另起一个子序列了。长度为1,dp值也就为1。
综上可得:
dp[i]=max(dp[j])+1,a[j]<=a[i]且,0<j<i.
i需要从开始到结尾O(n)枚举一遍,j需要从1到i枚举一遍。复杂度为双层for的O(n^2)
例题:
有n个数,求LIS:
输入:第一行n的值,第二行为n个数
输出:LIS长度。
代码:
#include<cstdio> #include<iostream> #include<cstring> #define ll long long using namespace std; int read() { int ans=0; char ch=getchar(),last=' '; while(ch<'0'||ch>'9')last=ch,ch=getchar(); while(ch>='0'&&ch<='9')ans=(ans<<3)+(ans<<1)+ch-'0',ch=getchar(); return last=='-'?-ans:ans; } int dp[100],a[100]; int n; //1 7 3 5 9 4 8 int main() { n=read(); for(int i=1;i<=n;i++) { a[i]=read(); } dp[1]=1; for(int i=2;i<=n;i++) { int maxn=-10; for(int j=1;j<i;j++) { if(a[j]<=a[i])maxn=max(maxn,dp[j]); } dp[i]=maxn==-10?1:maxn+1; } int maxn=-10; for(int i=1;i<=n;i++) { maxn=max(dp[i],maxn); } printf("%d",maxn); return 0; }
P1439 【模板】最长公共子序列
思路:看似是求公共子序列,实际上我们可以做这样1个转化:
我们把上面的序列顺次编号:
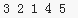
1 2 3 4 5
这样就变成的一个顺次递增的序列,并且我们获得了原序列和编号后的序列的转换法则:3对1,2对2,1对3。
我们在用这个法则处理一下下面的序列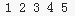
得到3 2 1 4 5
因为上面的序列1 2 3 4 5满足单调递增,所以只要下面的转换后的序列也满足单调递增,这个序列就是两个原序列的公共子序列,,
神奇吧。。。
于是我们只要求转化后的下面的序列的LIS就是答案。
O(n^2)算法:
#include<cstdio> #include<iostream> #include<cstring> #define ll long long #define N 100007 using namespace std; int read() { int ans=0; char ch=getchar(),last=' '; while(ch<'0'||ch>'9')last=ch,ch=getchar(); while(ch>='0'&&ch<='9')ans=(ans<<3)+(ans<<1)+ch-'0',ch=getchar(); return last=='-'?-ans:ans; } int n,a[N],b[N],c[N],d[N]; int main(){ n=read(); for(int i=1;i<=n;i++)a[i]=read(),c[a[i]]=i+10; for(int i=1;i<=n;i++)b[i]=read(); d[1]=1; for(int i=2;i<=n;i++)//求最长上升子序列 { int maxn=-1000; for(int j=1;j<i;j++) { if(c[b[j]]<=c[b[i]]) maxn=max(maxn,d[j]); } d[i]=(maxn==-1000?1:maxn+1); } int maxn=-1000; for(int i=1;i<=n;i++) { maxn=max(d[i],maxn); } printf("%d ",maxn); return 0; }
喜提:
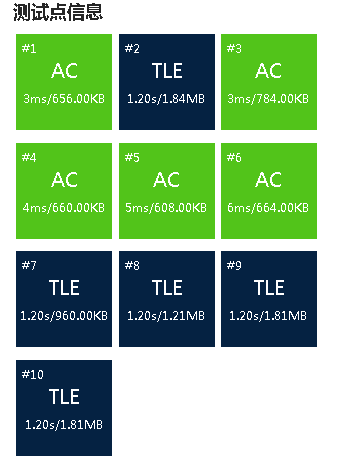
考虑
如果O(n^2)过了,你就可以踩标算了! 你可能用的神威太湖之光吧。
LIS优化:
我们上面的思路用的是枚举的方法,枚举之前最大的dp[i]。
事实上我们不用这么枚举,只需按照题目要求维护最大的长度len即可。
在之前,我已讲到了把上面的序列编号后对下面的序列进行转换,求最长上升子序列,我们继续:
考虑模拟一个栈stack,记录栈的深度len,
1.如果当前元素比栈顶大,就入栈,len++;
2.如果当前元素比栈顶小,二分查找第一个大于它的数,比较大小后插入栈。
因为第一个操作的缘故,所以栈中的元素始终满足单调递增,这也是可以二分的原因。
那么一个十分重要的问题:为什么这个方法可行?
上网搜了一些人的博客,好像都说简单易懂,什么立志讲解明白,但又好像都没讲懂。只能自己想了。
对于第一个操作,考虑每一个加入栈顶的元素,栈中的元素都比它小,它的到来肯定能使最长上升子序列的长度加一,所以len++;
对于第二个操作,考虑一个类似贪心的东西:你目前子序列长度就那样了(在不大于栈顶元素的情况下,自然对长度没啥影响),如果要使后面还没考虑到的部分能加入尽量多的元素来扩充长度,当前元素又比栈顶小,如果你二分后这个数的值比二分到栈中的值小,那么你何尝不替换掉和它,为后面的len++做准备呢?二分插入的元素
想到这,我又想到了一个问题:前面的元素数值又不会对len造成什么影响,你替换他干什么?
一个宏观的考虑:经过一系列替换,栈中的元素数值很定会普遍变小,最后影响len的栈顶也被替换变小。那么自然,更有利于后面的len++喽。
代码:
#include<cstdio> #include<iostream> #include<cstring> #define ll long long #define N 100007 using namespace std; int read() { int ans=0; char ch=getchar(),last=' '; while(ch<'0'||ch>'9')last=ch,ch=getchar(); while(ch>='0'&&ch<='9')ans=(ans<<3)+(ans<<1)+ch-'0',ch=getchar(); return last=='-'?-ans:ans; } int n,a[N],b[N],c[N],d[N],len=0; int main(){ // freopen("P1439_2.in","r",stdin); n=read(); for(int i=1;i<=n;i++)a[i]=read(),c[a[i]]=i+10; for(int i=1;i<=n;i++)b[i]=read(),d[i]=214748364; d[0]=0; for(int i=1;i<=n;i++) { int l=0,r=len,mid; if(c[b[i]]>d[len])d[++len]=c[b[i]]; else { while(l<r) { mid=(l+r)/2; if(d[mid]>c[b[i]])r=mid; else l=mid+1; } d[l]=min(c[b[i]],d[l]); } } printf("%d",len); return 0; }

过呢了是。(滑稽)
完结,希望对大家的理解和学习有所帮助。