P2939 [USACO09FEB]Revamping Trails G 题解 && 分层图入门讲解

考前补坑系列。之前懂分层图原理但是从来没写过，现在写一下。

---

题目传送门:

解题意：

给你一张非常正常的，n个点m条双向边的图，每条边有一个dis值，让你求1到n的最短路。

与普通最短路不同之处在于：在上述条件上，再加入一个k，在图中选取k条边使得边权变为0.

让你求最短路。

讲思路：

这里不再赘述正常的找思路过程，因为本文的目的不是解题而是为了介绍一个算法。

分层图，即字面意思，在原图的基础上，建立许许多多和原图完全相同的图。

你设想一下，把这些图竖着堆叠起来：

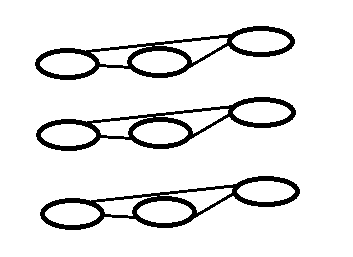
 原图为上图的其中一层，3个点大小的图。

我们要建立k层图，在上图中,k=2。

在此可能产生这样的问题：为啥要建k层？

题目中说要进行k次的把边变成0的操作，而题目往往不会给你模板让你去打，要不就是在模板的基础上魔改，要不就是结合多种算法求解。我们所要做的往往就是根据题意，进行准确的算法建模。在这道题中，与最短路不同的性质就是使k条边边权为0，我们要做的就是建出适合这个特殊性质的模型使得可以求解：

我们将上一层的from结点与下一层的to结点连边权为0双向边：

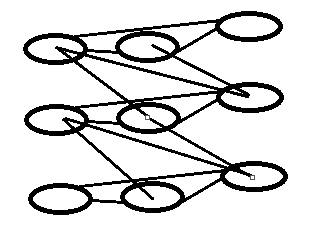
 设最上层的图为原图，即第一层，因为层间的边边权为0，那么从第一层走到第二层的效果是：经过了一个边权为0的边，而其他的边边权依旧是原来的边权。

没错，这也就代表着我们使用了一次使边免费的机会。

接着往后推：走到了第三层就代表着使用了2次边权免费的机会......走到了第k+1层就使用的k次机会。

至此，我们完成了切合题意的建模。

接下来考虑求解答案：因为可以使用k次，那么我们就从使用0次到使用k次的汇点（n）的dis值中取min即可。

分层图的点的编号只要保证可以用唯一的法则推出每一个点在每一层对应的编号即可。

自认为可读性高的代码：

#include<cstdio>
#include<cstring>
#include<iostream>
#include<queue>
#define N 10006
#define inf 2147483647
#define ll long long
using namespace std;
int read()
{
    int ans=0;
    char ch=getchar(),last=' ';
    while(ch>'9'||ch<'0')last=ch,ch=getchar();
    while(ch>='0'&&ch<='9')ans=(ans<<3)+(ans<<1)+ch-'0',ch=getchar();
    return last=='-'?-ans:ans;
}
int n,m,k,hea[210007],num,u,v,w,dis[210007],vis[210007];
struct edg{
    int nex,to,dis;
}edge[4100006];
struct node{
    int num,dis;
    bool operator < (const node &b)const{
        return dis>b.dis;
    }
};
inline void add(int from,int to,int dis)
{
    num++;
    edge[num].dis=dis;
    edge[num].nex=hea[from];
    edge[num].to=to;
    hea[from]=num;
}
inline void dij()
{
    memset(dis,0x3f,sizeof(dis));
    dis[1]=0;
    priority_queue<node> q;
    q.push((node){1,0});
    while(!q.empty())
    {
        node kk=q.top();q.pop();
        int now=kk.num;
        if(vis[now])continue;
        vis[now]=1;
        for(int i=hea[now];i;i=edge[i].nex)
        {
            int v=edge[i].to;
            if(dis[v]>dis[now]+edge[i].dis)
            {
                dis[v]=dis[now]+edge[i].dis;
                q.push((node){v,dis[v]});
            }
        }
    }
}
int main(){
    n=read();m=read(),k=read();
    for(int i=1;i<=m;i++)
    {
        u=read(),v=read(),w=read();
        add(u,v,w);add(v,u,w);
        for(int j=1;j<=k;j++)
        {
            add(j*n+u,j*n+v,w);
            add(j*n+v,j*n+u,w);
            add((j-1)*n+u,j*n+v,0);
        }
    }
    int ans=inf;
    dij();
    for(int i=0;i<=k;i++)
    {
        ans=min(ans,dis[(i+1)*n]);
    }
    printf("%d
",ans);
    return 0;
}

完结撒花，希望对各位有所帮助。

NOIP2020 冲鸭