刷题同时,总结一下状压。
在状压中发挥重要作用:位运算(&,|,^,~)常见的应用:
下面是由江苏省淮阴中学薛志坚整理的一些常见操作:
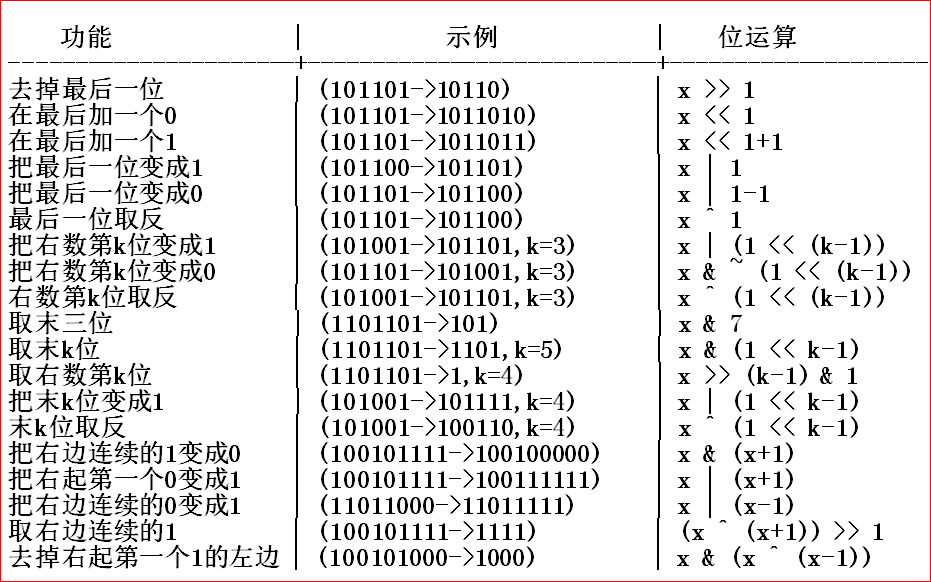
对于状压,什么是状压:一般基础的状压就是将一行状态,压成一个二进制数形式。最近做的题,基本涉及对于选不选的问题。
回到本题
状压 dp。把每一个人选不选压为二进制。
如 8 个人中选了 1,3 和 4 就可以表示为 00001101。
C[i] 表示当 i 这些人为一队时的总重量。T[i] 表示当 i 这些人为一队时里面最慢的那个人要的时间。
状态转移方程:
if(C[i ^ j] <= w) f[i] = min(f[i], f[j] + T[i ^ j]);
上代码:
#include <cstdio> #include <cstring> #include <string> #include <iostream> #include <algorithm> #define inf 2147483647 #define MAXN (1 << 16) + 1 using namespace std; int w, n, c[17], t[17]; int T[MAXN], C[MAXN], f[MAXN]; int max(int a, int b) { return a > b ? a : b; } int min(int a, int b) { return a < b ? a : b; } int main() { cin >> w >> n;; for (int i = 1; i <= n; ++i) cin >> t[i] >> c[i]; for (int i = 0; i < (1 << n); ++i) { int d = i, cnt = 0; while (d) { ++cnt; if (d & 1) { C[i] += c[cnt]; T[i] = max(T[i], t[cnt]); } d >>= 1; } f[i] = inf; } f[0] = 0; for (int i = 0; i < (1 << n); ++i) { for (int j = i; j >= 0; j = i & (j - 1)) { if (C[i ^ j] <= w) f[i] = min(f[i], f[j] + T[i ^ j]); if (j == 0) break; } } printf("%d ", f[(1 << n) - 1]); return 0; }
状压 dp。把每一个人选不选压为二进制。
如 8 个人中选了 1,3 和 4 就可以表示为 00001101。
C[i] 表示当 i 这些人为一队时的总重量。T[i] 表示当 i 这些人为一队时里面最慢的那个人要的时间。
状态转移方程:
if(C[i ^ j] <= w) f[i] = min(f[i], f[j] + T[i ^ j]);