已知椭圆 (C;dfrac{x^2}{a^2}+dfrac{y^2}{b^2}=1(a>b>0)) 的右焦点为 (F(1,0)) ,且经过点 (A(-2,0)) 和点 (B(2,0)) .
(1) 求椭圆 (C) 的方程;
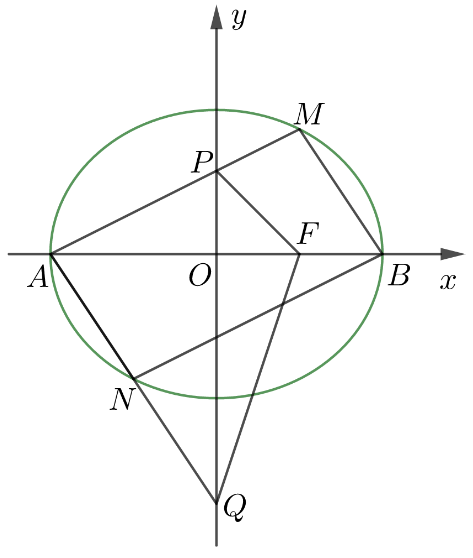
(2) (M) 和 (N) 是椭圆 (C) 上两个不同的点,四边形 (AMBN) 是平行四边形,直线 (AM,AN) 分别交 (y) 轴于点 (P) 和点 (Q) ,求四边形 (APFQ) 面积的最小值。
解析:
(1) (dfrac{x^2}{4}+dfrac{y^2}{3}=1) ;
(2) 法一:设 (M(x_0,y_0),N(-x_0,-y_0)) ,则
[k_{AM}cdot k_{AN}=dfrac{y_0}{x_0+2}cdotdfrac{-y_0}{-x_0+2}=dfrac{y_0^2}{x_0^2-4}
]
因为点 (M) 在椭圆上,则
[dfrac{x_0^2}{4}+dfrac{y_0^2}{3}=1Longrightarrow x_0^2-4=-dfrac{4y_0^2}{3}
]
则 (k_{AM}cdot k_{AN}=-dfrac{3}{4})直线,设直线 (AM) 的斜率 (k_{AM}=k(k>0)) ,则 (k_{AN}=-dfrac{3}{4k}) . 故有
[egin{cases}l_{AM}:y=k(x+2)\l_{AN}:y=-dfrac{3}{4k}(x+2)end{cases}Longrightarrowegin{cases} P(0,2k)\Q(0,-dfrac{3}{2k})end{cases}
]
则
[S_{APFQ}=dfrac12cdot|AF|cdot|PQ|=dfrac12cdot3cdot(2k+dfrac{3}{2k})geqslantdfrac32cdot2sqrt3=3sqrt3
]
当且仅当 (2k=dfrac{3}{2k}) ,(k=dfrac{sqrt3}{2}) 时,等号成立,四边形 (APFQ) 面积取最小值 (3sqrt3) .(由对称性得 (k=-dfrac{sqrt3}{2}) 时也成立)
法二:设 (M(x_0,y_0),N(-x_0,-y_0)) ,则
[k_{AM}=dfrac{y_0}{x_0+2};;,;; k_{AN}=dfrac{-y_0}{-x_0+2}
]
故得
[egin{cases}l_{AM}:y=dfrac{y_0}{x_0+2}(x+2)\[2ex]l_{AN}:y=dfrac{y_0}{x_0-2}(x+2)end{cases}Longrightarrowegin{cases} PBig(0,dfrac{2y_0}{x_0+2}Big)\[2ex]QBig(0,dfrac{2y_0}{x_0-2}Big)end{cases}
]
则
[S_{APFQ}=dfrac12cdot|AF|cdot|PQ|=dfrac12cdot3cdotBig|dfrac{2y_0}{x_0+2}-dfrac{2y_0}{x_0-2}Big|=dfrac{3}{2}Big|dfrac{-8y_0}{x_0^2-4}Big|
]
因为点 (M) 在椭圆上,则
[dfrac{x_0^2}{4}+dfrac{y_0^2}{3}=1Longrightarrow x_0^2-4=-dfrac{4y_0^2}{3}
]
所以
[S_{APFQ}=dfrac{9}{|y_0|}geqslant3sqrt3
]
当且仅当 (y_0=pmsqrt3) 时,四边形 (APFQ) 面积取最小值 (3sqrt3) .