给定一个由n个整点构成的凸多边形,求从n个点里任意选不少于3个点组成的所有凸多边形的面积之和,显然整点构成的多边形面积一定是0.5的整数倍,所以题目需要你算出答案的2倍 mod1000000007的值。
1.凸多边形里选出点组成的还是凸多边形。
2.三个点A,B,C构成的三角形,设从原点到他们的向量为fA,fB,fC,那么三角形面积的2倍就是fA×fB+fB×fC+fC×fA。
3.同理k个点(对应向量按逆时针排序为f1,f2,...,fk)构成的多边形面积的2倍等于 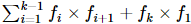
对于两个在原多边形上的点i,j,我们可以算出它们产生的贡献fi×fj在多少个需要多边形的式子里出现。 逆时针顺序在i和j之间的点都不能选,而且为了保证p≥3,所以按逆时针顺序在j到i这一段的点至少要有一个在多边形上。之后答案就是
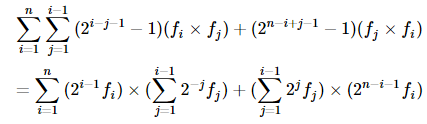
之后预处理一下2^n和前缀和就行了。