整个过程分七步,为了方便喜欢直接copy代码看结果的同学,每步都放上了完整的代码。
实验数据:
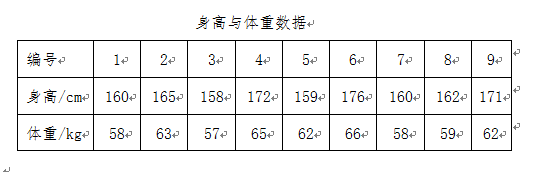
第一步:准备样本数据并绘制散点图
1)代码及其说明
import numpy as np import scipy as sp import matplotlib.pyplot as plt from scipy.optimize import leastsq ##样本数据(Xi,Yi),需要转换成数组(列表)形式 Xi=np.array([160,165,158,172,159,176,160,162,171]) #身高 Yi=np.array([58,63,57,65,62,66,58,59,62])#体重 #画样本点 plt.figure(figsize=(8,6)) ##指定图像比例: 8:6 plt.scatter(Xi,Yi,color="green",label="样本数据",linewidth=1) plt.show()
2)结果图

3)分析
从散点图可以看出,样本点基本是围绕箭头所示的直线分布的。所以先以直线模型对数据进行拟合
第二步: 使用最小二乘法算法求拟合直线
1)代码及其说明
import numpy as np import scipy as sp import matplotlib.pyplot as plt from scipy.optimize import leastsq ##样本数据(Xi,Yi),需要转换成数组(列表)形式 Xi=np.array([160,165,158,172,159,176,160,162,171]) Yi=np.array([58,63,57,65,62,66,58,59,62]) ##需要拟合的函数func :指定函数的形状 k= 0.42116973935 b= -8.28830260655 def func(p,x): k,b=p return k*x+b ##偏差函数:x,y都是列表:这里的x,y更上面的Xi,Yi中是一一对应的 def error(p,x,y): return func(p,x)-y #k,b的初始值,可以任意设定,经过几次试验,发现p0的值会影响cost的值:Para[1] p0=[1,20] #把error函数中除了p0以外的参数打包到args中(使用要求) Para=leastsq(error,p0,args=(Xi,Yi)) #读取结果 k,b=Para[0] print("k=",k,"b=",b) #画样本点 plt.figure(figsize=(8,6)) ##指定图像比例: 8:6 plt.scatter(Xi,Yi,color="green",label="样本数据",linewidth=2) #画拟合直线 x=np.linspace(150,190,100) ##在150-190直接画100个连续点 y=k*x+b ##函数式 plt.plot(x,y,color="red",label="拟合直线",linewidth=2) plt.legend() #绘制图例 plt.show()
2)结果图

3)分析
从图上看,拟合效果还是不错的。样本点基本均匀的分布在回归线两边,没有出现数据点严重偏离回归线的情况。
第三步: 验证回归线的拟合程度—残差分布图
1)代码及其说明
import numpy as np import matplotlib.pyplot as plt import statsmodels.api as sm from statsmodels.graphics.api import qqplot ##样本数据(Xi,Yi),需要转换成数组(列表)形式 Xi=np.array([160,165,158,172,159,176,160,162,171]) Yi=np.array([58,63,57,65,62,66,58,59,62]) xy_res=[] ##计算残差 def residual(x,y): res=y-(0.42116973935*x-8.28830260655) return res ##读取残差 for d in range(0,len(Xi)): res=residual(Xi[d],Yi[d]) xy_res.append(res) ##print(xy_res) ##计算残差平方和:22.8833439288 -->越小拟合情况越好 xy_res_sum=np.dot(xy_res,xy_res) #print(xy_res_sum) ##如果数据拟合模型效果好,残差应该遵从正态分布(0,d*d:这里d表示残差) #画样本点 fig=plt.figure(figsize=(8,6)) ##指定图像比例: 8:6 ax=fig.add_subplot(111) fig=qqplot(np.array(xy_res),line='q',ax=ax) plt.show()
2)结果图
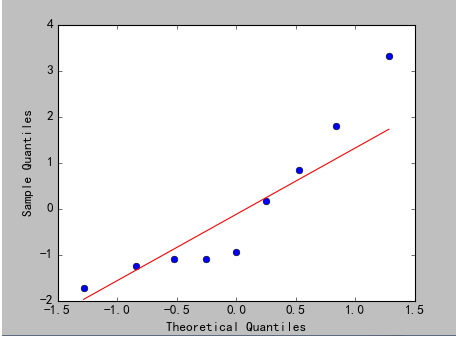
3)分析
上图为Q-Q图,原理:如果两个分布相似,则该Q-Q图趋近于落在y=x线上。如果两分布线性相关,则点在Q-Q图上趋近于落在一条直线上,但不一定在y=x线上。Q-Q图可以用来可在分布的位置-尺度范畴上可视化的评估参数。
从图上可以看出,回归效果比较理想,但不是最理想的
4)以下代码可以同样实现上述图示:
import numpy as np import scipy.stats as stats import pylab ##样本数据(Xi,Yi),需要转换成数组(列表)形式 Xi=np.array([160,165,158,172,159,176,160,162,171]) Yi=np.array([58,63,57,65,62,66,58,59,62]) xy_res=[] ##计算残差 def residual(x,y): res=y-(0.42116973935*x-8.28830260655) return res ##读取残差 for d in range(0,len(Xi)): res=residual(Xi[d],Yi[d]) xy_res.append(res) ##print(xy_res) ##计算残差平方和:22.8833439288 -->越小拟合情况越好 xy_res_sum=np.dot(xy_res,xy_res) #print(xy_res_sum) ##如果数据拟合模型效果好,残差应该遵从正态分布(0,d*d:这里d表示残差) #画样本点 stats.probplot(np.array(xy_res),dist="norm",plot=pylab) pylab.show()
第四步: 验证回归线的拟合程度—标准化残差
1)代码及其说明
import numpy as np import matplotlib.pyplot as plt ##样本数据(Xi,Yi),需要转换成数组(列表)形式 Xi=np.array([160,165,158,172,159,176,160,162,171]) Yi=np.array([58,63,57,65,62,66,58,59,62]) xy_res=[] ##计算残差 def residual(x,y): res=y-(0.42116973935*x-8.28830260655) return res ##读取残差 for d in range(0,len(Xi)): res=residual(Xi[d],Yi[d]) xy_res.append(res) ##print(xy_res) ##计算残差平方和:22.8833439288 -->越小拟合情况越好 xy_res_sum=np.dot(xy_res,xy_res) ''' 标准残差: (残差-残差平均值)/残差的标准差 ''' ''' 标准残差图: 1.标准残差是以拟合模型的自变量为横坐标,以标准残差为纵坐标形成的平面坐标图像 2.试验点的标准残差落在残差图的(-2,2)区间以外的概率<=0.05.若某一点落在区间外,可判为异常点 3.有效标准残差点围绕y=0的直线上下完全随机分布,说明拟合情况良好 4.如果拟合方程原本是非线性模型,但拟合时却采用了线性模型,标准化残差图就会表现出曲线形状,产生 系统性偏差 ''' ##计算残差平均值 xy_res_avg=0 for d in range(0,len(xy_res)): xy_res_avg+=xy_res[d] xy_res_avg/=len(xy_res) #残差的标准差 xy_res_sd=np.sqrt(xy_res_sum/len(Xi)) ##标准化残差 xy_res_sds=[] for d in range(0,len(Xi)): res=(xy_res[d]-xy_res_avg)/xy_res_sd xy_res_sds.append(res) #print(xy_res_sds) #标准化残差分布 plt.figure(figsize=(8,6)) ##指定图像比例: 8:6 plt.scatter(Xi,xy_res_sds) plt.show() ''' 1.绝大部分数据分布在(-2,+2)的水平带状区间内,因此模型拟合较充分 2.数据点分布稍均匀,但没有达到随机均匀分布的状态。此外,部分数据点还呈现某种曲线波动形状, 有少许系统性偏差。因此可能采用非线性拟合效果会更好 '''
2)结果图
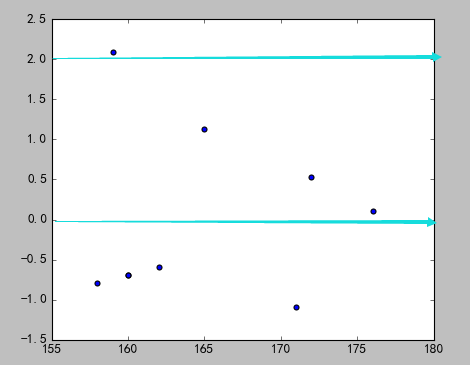
3)分析
数据点分布还是存在一定的变化趋势的。
第五步:使用曲线模型拟合数据
1)代码及其说明
import numpy as np import scipy as sp import matplotlib.pyplot as plt from scipy.optimize import leastsq ##样本数据(Xi,Yi),需要转换成数组(列表)形式 Xi=np.array([160,165,158,172,159,176,160,162,171]) Yi=np.array([58,63,57,65,62,66,58,59,62]) ##需要拟合的函数func :指定函数的形状 k= 0.860357336936 b= -19.6659389666 def func(p,x): k,b=p return x**k+b ##偏差函数:x,y都是列表:这里的x,y更上面的Xi,Yi中是一一对应的 def error(p,x,y): return func(p,x)-y #k,b的初始值,可以任意设定,经过几次试验,发现p0的值会影响cost的值:Para[1] p0=[1,20] #把error函数中除了p0以外的参数打包到args中(使用要求) Para=leastsq(error,p0,args=(Xi,Yi)) #读取结果 k,b=Para[0] print("k=",k,"b=",b) #画样本点 plt.figure(figsize=(8,6)) ##指定图像比例: 8:6 plt.scatter(Xi,Yi,color="green",label="样本数据",linewidth=2) #画拟合直线 x=np.linspace(150,190,100) ##在150-190直接画100个连续点 y=x**k+b ##函数式 plt.plot(x,y,color="red",label="拟合直线",linewidth=2) plt.legend() #绘制图例 plt.show()
2)结果图
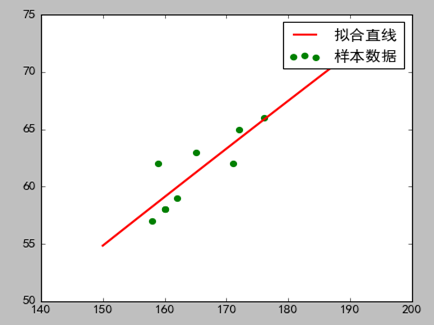
3)分析
由于标准化残差的分布图,部分数据的趋势与幂函数在第一象限的图像类似, 所以采用了y=xa +b的函数形式,截距b是为了图像可以在Y轴上下移动
第六步:验证回归线的拟合程度—残差分布图
1)代码及其说明
import numpy as np import matplotlib.pyplot as plt import statsmodels.api as sm from statsmodels.graphics.api import qqplot ##样本数据(Xi,Yi),需要转换成数组(列表)形式 Xi=np.array([160,165,158,172,159,176,160,162,171]) Yi=np.array([58,63,57,65,62,66,58,59,62]) xy_res=[] ##计算残差 def residual(x,y): res=y-(x**0.860357336936-19.6659389666) return res ##读取残差 for d in range(0,len(Xi)): res=residual(Xi[d],Yi[d]) xy_res.append(res) ##print(xy_res) ##计算残差平方和:22.8833439288 -->越小拟合情况越好 xy_res_sum=np.dot(xy_res,xy_res) #print(xy_res_sum) ##如果数据拟合模型效果好,残差应该遵从正态分布(0,d*d:这里d表示残差) #画样本点 fig=plt.figure(figsize=(8,6)) ##指定图像比例: 8:6 ax=fig.add_subplot(111) fig=qqplot(np.array(xy_res),line='q',ax=ax) plt.show()
2)结果图
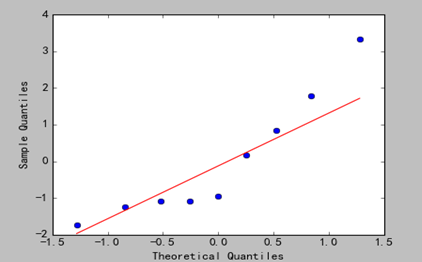
3)分析
从图上可以看出,回归效果也比较理想
第七步:验证回归线的拟合程度—标准化残差
1)代码及其说明
import numpy as np import matplotlib.pyplot as plt ##样本数据(Xi,Yi),需要转换成数组(列表)形式 Xi=np.array([160,165,158,172,159,176,160,162,171]) Yi=np.array([58,63,57,65,62,66,58,59,62]) xy_res=[] ##计算残差 def residual(x,y): res=y-(x**0.860357336936-19.6659389666) return res ##读取残差 for d in range(0,len(Xi)): res=residual(Xi[d],Yi[d]) xy_res.append(res) ##print(xy_res) ##计算残差平方和:22.881076636 -->越小拟合情况越好 xy_res_sum=np.dot(xy_res,xy_res) #print(xy_res_sum) ''' 标准残差: (残差-残差平均值)/残差的标准差 ''' ##计算残差平均值 xy_res_avg=0 for d in range(0,len(xy_res)): xy_res_avg+=xy_res[d] xy_res_avg/=len(xy_res) #残差的标准差 xy_res_sd=np.sqrt(xy_res_sum/len(Xi)) ##标准化残差 xy_res_sds=[] for d in range(0,len(Xi)): res=(xy_res[d]-xy_res_avg)/xy_res_sd xy_res_sds.append(res) print(xy_res_sds) #标准化残差分布 plt.figure(figsize=(8,6)) ##指定图像比例: 8:6 plt.scatter(Xi,xy_res_sds) plt.show() ''' 1.绝大部分数据分布在(-2,+2)的水平带状区间内,因此模型拟合较充分 2.数据点分布稍均匀,但没有达到随机均匀分布的状态。此外,部分数据点还呈现某种曲线波动形状, 有少许系统性偏差。因此可能采用非线性拟合效果会更好 '''
2)结果图
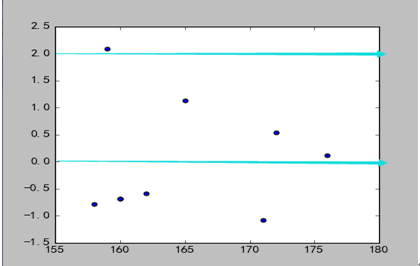
3)分析
数据点分布趋和直线回归方程基本一样
补充说明:
其实整个实验过程并没有达到预期效果。
1)如果对实验过程的5-7步使用R语言重新实验(R语言提供了所有相关函数),第7步的效果如下:

也就说所有的标准化残差都是落在(-2,+2)区间内的,即曲线方程才是最佳拟合方程。
2)标准化残差没有找到具体的定义,网上对这个定义有多种解释
3)标准化残差的计算方式没有找到相应的python包,只能按照其中某一个定义自己写代码计算(估计是浮点数计算产生的误差)