在线性回归问题中比较常用的一种算法就是最小二乘法(OLS),其核心思想是:通过最小化误差的平方和寻找数据的最佳函数匹配。
但是普通的OLS最常见的一个问题是容易过度拟合：即在样本数据集上属性值(x)和目标值(y)是一一对应的。这样的结果看似拟合效果
很好，但是在新数据集上的误差却会很大。
解决这个问题，目前主要有两种思路：前向逐步回归和惩罚线性回归。之所以说是两种思路，而不是两种算法，是因为以这两种思想
为基础，形成了两种算法族，尤其是后者有多种较出名的算法(例如岭回归、套索回归、最小角度回归、Glmnet等)。
前向逐步回归基本算法思路：遍历属性中的每一列，找到均方误差(MSE)之和最小的一列(即效果最佳的列)，然后寻找和这列组合效果
最好的第二列属性，依次类推直到所有的列。在这个过程中MSE--属性个数在坐标系中行成的曲线会有明显的变化，可以通过观察曲线得到
想要的结果，或者通过打印出来的MES值获得最终结果。
惩罚线性回归基本算法思路：在普通最小二乘法的公式中添加一个惩罚项。如果最小二乘法以下面的数学公式表达：
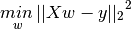，那么套索(Lasso)回归的公式为：
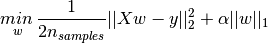.其中，α||W||=α(|w1|+|w2|+...+|Wn|)。
Lasso通过构造一个惩罚函数得到一个较为精炼的模型，使得它压缩一些系数，同时设定一些系数为零，也就是说Lasso的系数向量是稀疏的。
Lasso是采用的L1范数正则化(OLS在变量选择方面的三种扩展方法中的一种,也叫收缩方法）： L1范数是指向量中各个元素绝对值之和。
上面说了关于模型的问题，下面说说模型评估。
目前主要的模型性能评估方法也有两种：预留测试集和n折交叉验证。
预留测试集就是把样本数据分成两类：一类用于训练模型，另一类用于测试模型。一般情况下测试集可以占所有数据的25%～35%。
n折交叉验证就是把数据分成n份不相交的子集，以其中的一份作为测试集，另外n-1份作为训练集。假如把数据分成5份，依次编号1～5，第一次把1号作为测试集，2、3、4、5号作为训练集，第二次把2号作为测试集，1、3、4、5作为训练集，依次类推，直到结束。
这里的功能核心是：sklearn.linear_model.LassoCV
LassoCV参数有很多，我们只用用到参数cv：表示使用几折交叉验证。
重点是介绍下相关属性：
alpha_: 通过交叉验证后得到的处罚系数，即公式中的α值
coef_: 参数向量（公式中的w）
mse_path_: 每次交叉验证的均方误差
alphas_: 验证过程中使用过的alpha值
本次测试相关的理论基础大概就这么多，下面开始实验：数据来源
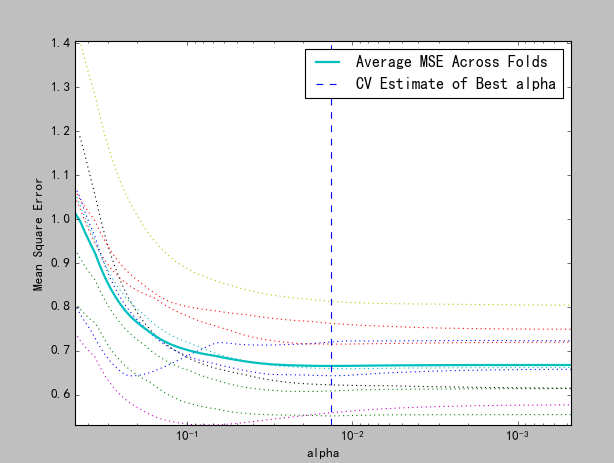
import numpy as np import matplotlib.pyplot as plt from sklearn import linear_model from sklearn.linear_model import LassoCV import os ##运行脚本所在目录 base_dir=os.getcwd() data=np.loadtxt(base_dir+r"wine.txt",delimiter=";") ##矩阵的长度：行数 dataLen = len(data) ##矩阵的宽度：列数 dataWid = len(data[0]) ##每列的均值 xMeans = [] ##每列的方差 xSD = [] ##归一化样本集 xNorm = [] ##归一化标签 lableNorm = [] ##第一次处理数据：计算每列的均值和方差 for j in range(dataWid): ##读取每列的值 x = [data[i][j] for i in range(dataLen)] ##每列的均值 mean = np.mean(x) xMeans.append(mean) ##每列的方差 sd = np.std(x) xSD.append(sd) ##第二次处理数据：归一化样本集和标签 for j in range(dataLen): ##样本集归一化 xn = [(data[j][i]-xMeans[i])/xSD[i] for i in range(dataWid-1)] xNorm.append(xn) ##标签归一化 ln = (data[j][dataWid-1]-xMeans[dataWid-1])/xSD[dataWid-1] lableNorm.append(ln) ##参数格式是数组形式，所以需要转换一下 X=np.array(xNorm) Y=np.array(lableNorm) ##开始做交叉验证：cv=10表示采用10折交叉验证 wineModel = LassoCV(cv=10).fit(X,Y) ##打印出最佳解的每项的系数：[ 0,-0.22773828,0,0,-0.09423888, ##0.02215153,-0.09903605,0,-0.06787363,0.16804092,0.3750958 ] print(wineModel.coef_) ##打印出最佳解的惩罚系数：0.013561387701 print(wineModel.alpha_) ##绘图 plt.figure() ##随着alpha值的变化，均方误差的变化曲线 plt.plot(wineModel.alphas_, wineModel.mse_path_, ':') ##验证过程中，随着alpha值的变化，均方误差的平均曲线 plt.plot(wineModel.alphas_, wineModel.mse_path_.mean(axis=-1), label='Average MSE Across Folds', linewidth=2) ##每次验证系统认为的最合适的alpha值 plt.axvline(wineModel.alpha_, linestyle='--', label='CV Estimate of Best alpha') plt.semilogx() plt.legend() ax = plt.gca() ax.invert_xaxis() plt.xlabel('alpha') plt.ylabel('Mean Square Error') plt.axis('tight') plt.show()
最佳解的惩罚系数和向量系数已经在代码中以注释的方式写了，生成的结果图如下：
