修剪草坪

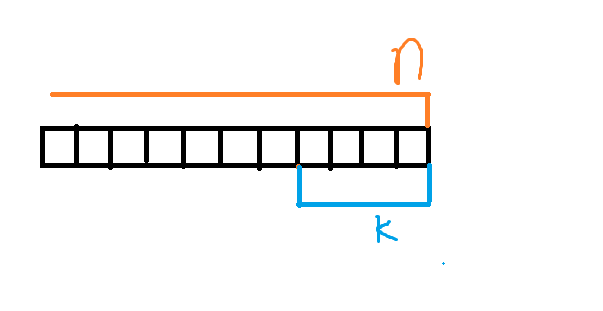
f[i][0],f[i][1]表示第i格奶牛选还是不选,

f[i][0]=max(f[i-1][1],f[i-1][0]);

f[i][1]=max(f[j][0]+sum[i]-sum[j])   i-k<=j<i   --->    f[i][1]=max(f[j][0]-sum[j])+sum[i]    i-k<=j<i   这样就可以用单调队列优化了

这里j<i用先算再加来实现

#include<iostream>
#include<cstdio>
using namespace std;
typedef long long ll;
const int maxn=1e5+7;
ll e[maxn],f[maxn][2],sum[maxn];
ll n,k;
int head=1,tail=1,q[maxn];
int main(){
    cin>>n>>k;
    for(int i=1;i<=n;i++) {cin>>e[i];sum[i]=sum[i-1]+e[i];}
    for(int i=1;i<=n;i++){
        f[i][0]=max(f[i-1][0],f[i-1][1]);
        while(head<=tail&&q[head]<i-k) head++;  
        f[i][1]=f[q[head]][0]-sum[q[head]]+sum[i];
        while(head<=tail&&f[i][0]-sum[i]>=f[q[tail]][0]-sum[q[tail]]) tail--;
        q[++tail]=i; 
    }
    cout<<max(f[n][0],f[n][1])<<endl;
    return 0;
} 

第14行q[head]<i-k是没有等号的