codeforce 437B The Child and Set

time limit per test

1 second

memory limit per test

256 megabytes

input

standard input

output

standard output

At the children's day, the child came to Picks's house, and messed his house up. Picks was angry at him. A lot of important things were lost, in particular the favorite set of Picks.

Fortunately, Picks remembers something about his set S:

• its elements were distinct integers from 1 to limit;
• the value of 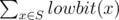 was equal to sum; here lowbit(x) equals 2^k where k is the position of the first one in the binary representation of x. For example, lowbit(10010₂) = 10₂, lowbit(10001₂) = 1₂, lowbit(10000₂) = 10000₂ (binary representation).

Can you help Picks and find any set S, that satisfies all the above conditions?

在儿童节这一天，我们的小朋友来到了Picks的家，把他家里弄得一团糟。Picks非常生气。非常多重要的东西都不见了，这当中包含了Picks最喜欢的集合。

幸运的是，Picks记得一些关于他的集合S的事情：
1. 其元素是1至limit间的互异整数；
2. 全部lowbit(x)之和（x取遍S中的全部元素）等于sum，这里lowbit(x)等于2^k，k是x的二进制表示中第一个1的位置。比如（下面数字均为二进制表示），lowbit(10010)=10，lowbit(10001)=1，lowbit(10000)=10000。
你能帮助Picks找到一个符合上述条件的集合S吗？

Input

The first line contains two integers: sum, limit (1 ≤ sum, limit ≤ 10⁵). 一行，两个整数，依次是sum和limit(1<=sum,limit<=10^5)。

Output

In the first line print an integer n (1 ≤ n ≤ 10⁵), denoting the size of S. Then print the elements of set S in any order. If there are multiple answers, print any of them.

If it's impossible to find a suitable set, print -1.

第一行输出n(1<=n<=10^5)，为集合S的大小。然后在下一行以随意顺序输出S的全部元素。假设有多个符合要求的集合，输出随意一个就可以。
假设找不到这种集合，输出-1。

Sample test(s)

input

5 5

output

2
4 5

input

4 3

output

3
2 3 1

input

5 1

output

-1

Note

In sample test 1: lowbit(4) = 4, lowbit(5) = 1, 4 + 1 = 5.

In sample test 2: lowbit(1) = 1, lowbit(2) = 2, lowbit(3) = 1, 1 + 2 + 1 = 4.

题解

lowbit就是x&（-x）。其余为模拟。

#include<cstdio>
#include<cstring>
#include<cstdlib>
#include<iostream>
#include<cmath>
#include<algorithm>
using namespace std;
int m,l,ans[100002];
struct shu {int w,b;} a[100002];
int lowbit(int x) {return x&(-x);}
bool kp(const shu &x,const shu &y)
{return x.b>y.b;}
void doit()
{
	sort(a+1,a+l+1,kp);
	for(int i=1;i<=l;i++)
	   {if(m>=a[i].b)
	       {m-=a[i].b;
		    ans[++ans[0]]=a[i].w;
		   }
	   }
	if(m)printf("-1");
	else 
	{
		printf("%d
",ans[0]);
		for(int i=1;i<=ans[0];i++)
		    printf("%d ",ans[i]);
	} 
}
int main()
{
	scanf("%d%d",&m,&l);
	for(int i=1;i<=l;i++)
	   {a[i].w=i; a[i].b=lowbit(i);}
	doit();
	return 0;
}