codeforces Round #259(div2) C解题报告

C. Little Pony and Expected Maximum

time limit per test

 1 second

memory limit per test

 256 megabytes

input

 standard input

output

 standard output

Twilight Sparkle was playing Ludo with her friends Rainbow Dash, Apple Jack and Flutter Shy. But she kept losing. Having returned to the castle, Twilight Sparkle became interested in the dice that were used in the game.

The dice has m faces: the first face of the dice contains a dot, the second one contains two dots, and so on, the m-th face contains mdots. Twilight Sparkle is sure that when the dice is tossed, each face appears with probability 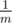. Also she knows that each toss is independent from others. Help her to calculate the expected maximum number of dots she could get after tossing the dice n times.

Input

A single line contains two integers m and n (1 ≤ m, n ≤ 105).

Output

Output a single real number corresponding to the expected maximum. The answer will be considered correct if its relative or absolute error doesn't exceed 10  - 4.

Sample test(s)

input

6 1

output

3.500000000000

input

6 3

output

4.958333333333

input

2 2

output

1.750000000000

Note

Consider the third test example. If you've made two tosses:

1. You can get 1 in the first toss, and 2 in the second. Maximum equals to 2.
2. You can get 1 in the first toss, and 1 in the second. Maximum equals to 1.
3. You can get 2 in the first toss, and 1 in the second. Maximum equals to 2.
4. You can get 2 in the first toss, and 2 in the second. Maximum equals to 2.

The probability of each outcome is 0.25, that is expectation equals to:

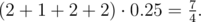
You can read about expectation using the following link: http://en.wikipedia.org/wiki/Expected_value

题目大意：

一个m个面的骰子。抛掷n次，求这n次里最大值的期望是多少。

解法：

数学题，有m个面的骰子。抛n次，那么总共的情况就有m^n。

我们从m=1開始推起。

m = 1， 仅仅有一种情况。

m = 2。新增了2^n-1^n种情况。这些新增的情况里面。最大值均是 2，

m = 3，新增了3^n-2^n种情况。这些新增的情况里面，最大值均是 3。

我们就能够推出数学期望公式：  ans = 1/(m^n) * [1 + (2^n-1^n)*2 + (3^n-2^n)*3 .... + (m^n - (m-1)^n)*m]

但m^n太大，我们得改变一下式子。 ans = (1/m)^n - (0/m)^n + [(2/m)^n - (1/m)^n] * 2 ...... + [(m/m)^n - ((m-1)/m)^n] * m。

代码：

#include <cstdio>
#include <cmath>

using namespace std;

double n, m, ans;

int main() {
	scanf("%lf%lf", &m, &n);

	ans = pow(1.0/m, n);
	for (int i = 2; i <= m; i++)
		ans += (pow(i/m, n) - pow((i-1)/m, n)) * i;
	printf("%lf", ans);
}