这是一道dfs,但是...但是....但是它竟然被放在bfs练习题辣!!!!
打了半天bfs,发现路径不会标记了,于是发现好像有什么不对的,似乎dfs要简单一点,于是半路跑去打dfs,结果打了半天没有输出。。。。又跑回来打bfs。。。。如此循环n遍,甚至找了bfs的题解,但是...蒟蒻到看不懂。回去深思dfs,突然发现没有把走过的路径标记下来......崩溃.....悲伤......&%&^$&^&*^*%&^%(&*^*&%&&^^&((^*&(&*^&^&%&^#$%$$^&%^#$^&(*&^(*^&^&&*(&*()
(某人崩溃到乱码ing)
好了刚才我什么都没有说。
为什么说这道题不是bfs而是dfs呢?
首先,题目要求的是走到终点的方案数,而不是最小步数
如果是求最小步数,那当然是用bfs了。但这里求的是方案数,也就是走到一次终点,ans++,然后把这条路径重新标记为没走过。(回溯)用bfs,也就是把每一步的坐标加入队列。为什么说他不方便回溯呢?这和bfs的搜索顺序有关
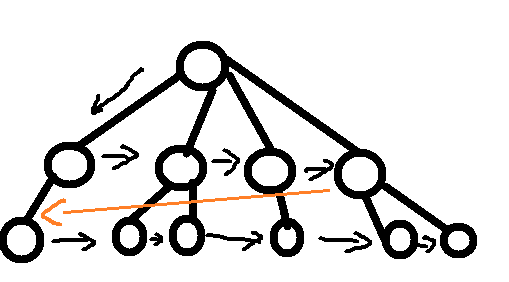
箭头为bfs每个节点出现的顺序,所以当我们用bfs走到出口时,会发现该节点的父亲节点的位置已经跑到十万八千里之外了,并且还不能由出队得到父亲节点。
当然,这里有位大神用bfs做的。bfs题解(这是所有的题解...)
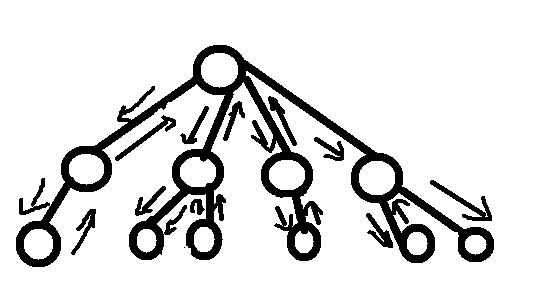
这是dfs每个节点出现的顺序,这样回溯到父亲节点就简单多了,直接回溯一步就行,所以这个题选用dfs解法(也就是套个模板)
在此复习一下dfs的模板(from c++一本通)
模板一:
int dfs(k) { for(int i=1;i<=maxn;i++)//maxn是变化方式的总数 {if(操作合法) {保存结果; if(到达目的地) {输出解;return 0; } dfs(k+1); 回溯; } } }
模板二:
void dfs(k) { if(到达目标){输出解; return;} for(int i=1;i<=maxn;i++) { if(操作合法) {标记; dfs(k+1); 回溯; } } }
好了我们开始套模板
#include<iostream> #include<cstdio> using namespace std; int k,n,m,t,sx,sy,fx,fy,dx[4]={1,-1,0,0},dy[4]={0,0,1,-1},ans,ljx[100001],ljy[100001]; int zx[26],zy[26]; bool vis[26][26],bl[26][26]; bool hf(int x,int y) { if(x<1||x>n||y<1||y>m)return 0; for(int i=1;i<=t;i++) if(x==zx[i]&&y==zy[i])return 0; if(vis[x][y])return 0; return 1; } void search(int x,int y) { if(x==fx&&y==fy)//一个模板 {ans+=1;vis[x][y]=1;return ; } for(int i=0;i<=3;i++)//四个方向 { int xx=x+dx[i],yy=y+dy[i];//从当前的x,y向四个方向走(走到下一步时的x与y就是这一步的xx和yy,所以不必有x+=dx[i],y+=dy[i] if(hf(xx,yy)) { vis[xx][yy]=1;//在判断中以是否走过为主要依据 (原因:每个格只走一次) search(xx,yy); vis[xx][yy]=0;//回溯 } } } int main() { scanf("%d%d%d",&n,&m,&t); scanf("%d%d%d%d",&sx,&sy,&fx,&fy); for(int i=1;i<=t;i++) {scanf("%d%d",&zx[i],&zy[i]); vis[zx[i]][zy[i]]=1;//标记走过 } vis[sx][sy]=1; search(sx,sy); printf("%d",ans); }
qwq