讲了半天好像也许maybe听懂了一点,先写下来233
先整理整理怎么存(开始绕)
最简单的是邻接矩阵存,但是开到10000*10000就MLE了,所以我们用链式前向星存(据说是叫这个名字吧)
这是个什么鬼玩意呢?
我们在记录时,以输入的顺序记录。
我们记录一条边,就记下它的终点(to),权值(就是边长)(dis),以及和这条边的起点相同,编号稍微小一点的边的编号(next)(开始绕)
这里我们记录当前每个点的所有出边(就是起点是这个点的边)中编号最大的那一条边(因为上面的next是编号稍微小的边)
当然也可以依据自己的习惯存储边
先上段代码
int head[nmax],n,m,s;//head[i] 是 以 点 i 为 起 点 , 所 有 出 边 中 编 号 最 大 的 一 个 priority_queue<pair<int,int> > q; void add(int fr,int _to,int _dis) { cnt++; eage[cnt].to=_to; eage[cnt].dis=_dis; eage[cnt].next=head[fr];//fr 为 from 的 简 写 , 这 里 的 以 点 i 为 起 点 的 边 多 了 一 条, //所 以 上 一 个 以 点 i 为 起 点 的 编 号 最 大 的 边 就 是 这 里 的 以 i 为 起 点 编 号 最 大 的 边 的 上 一 条 边 head[fr]=cnt; //更 新 head[i] }Edge [50001]; const int inf=2147483647; int main() { scanf("%d%d%d",&n,&m,&o_node); dis[o_node]=0; for(int i=1;i<=m;i++) {int from,to,dis; cin>>from>>to>>dis; add(from,to,dis); }
这一坨是存图
拿张图举个例子
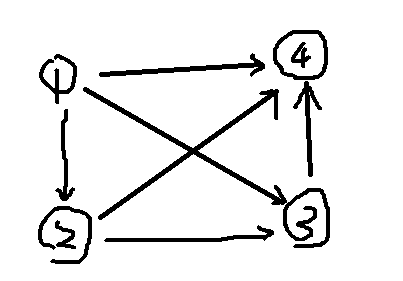
假设我们输入边的数据如下(三个数n,m,s,n为起点,m为终点,s为边长)
1 2 2
2 3 2
1 3 5
2 4 1
3 4 2
1 4 4
那代码中的存储如下
Edge[1].to=2,Edge[1].dis=2,Edge[1].next=0,head[1]=1(这里指没有上一条边),head[1]=1(这里head[i]记录的是以i为起点,当前最大编号出边的编号)
Edge[2].to=3,Edge[2].dis=2,Edge[2].next=0,head[2]=2
Edge[3].to=3,Edge[3].dis=5,Edge[3].next=1,head[1]=3
.....................................
讲完存图,再来说这个算法是怎么实现的
要求最短路径,这里有点类似贪心。
首先选择一个距离起点最近的直达点b,记录当前点与b的距离,再由b进行相同的扩展,来更新起点与其它点的距离
这样更新了一圈后就是最短距离,
再举个栗子
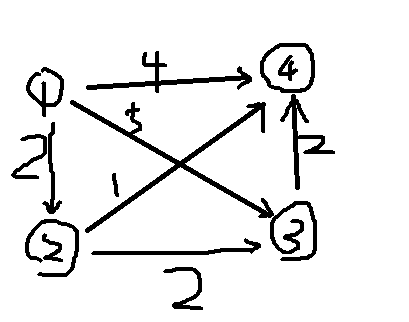
没错还是刚才那张图,这里标出了每条边的权值
按照dijkstra算法,我们首先找到距离①最近的直达点②,由②更新出①到④的最短路为3,①到③的最短路为4,
那么程序怎么实现呢?
看注释吧
(代码from gh,注释自己加的)
#include <iostream> #include <cstdio> #include <queue> using namespace std; const int INF = 2147483647; struct edge { int to, dis_, next; } Edge[500001]; struct node { int to, dis; inline friend bool operator<(const node &a, const node &b) { return a.dis < b.dis;//构造函数,将优先队列按照权值从小到大排序 } }; int head[500001], dis[10001]; bool vst[10001]; int nodenum, edgenum, origin_node, cnt = 1; priority_queue<node> q;//优先队列 inline void add_edge(int from, int to, int value) { Edge[cnt].to = to; Edge[cnt].dis_ = value; Edge[cnt].next = head[from]; head[from] = cnt++; } inline void dijkstra() { for (register int i = 1; i < origin_node; i++) { dis[i] = INF;//全部初始化为一个很大的数 } dis[origin_node]=0; for (register int i = origin_node + 1; i <= nodenum; i++) { dis[i] = INF; } q.push((node){origin_node, 0}); while (!q.empty())//队不空(这里是当广搜来做的) { int x = q.top().to; q.pop(); if (vst[x])//如果访问过,就跳过 continue; vst[x] = 1; for (register int i = head[x]; i; i = Edge[i].next)//从以x为起点的最后一条边开始,一直遍历完这个点的所有边 { dis[Edge[i].to] = min(dis[Edge[i].to], dis[x] + Edge[i].dis_);//比较原来的大小和以x点为中转后的大小(取小的) q.push((node){Edge[i].to, -dis[Edge[i].to]});//入队 } } } template <typename T_> inline T_ getnum() { T_ res = 0; bool flag = false; char ch = getchar(); while (!isdigit(ch)) { flag = flag ? flag : ch == '-'; ch = getchar(); } while (isdigit(ch)) { res = (res << 3) + (res << 1) + ch - '0'; ch = getchar(); } return flag?-res:res; } template<typename T_> inline void putnum(T_ num) { if (num<0) { putchar('-'); num=-num; } if (num>9)putnum(num/10); putchar('0'+num%10); } int main() { nodenum = getnum<int>(), dgenum = getnum<int>(),origin_node = getnum<int>(); for (register int i = 1; i <= edgenum; i++) { register int f, t, v; f = getnum<int>(), t = getnum<int>(), v = getnum<int>(); add_edge(f, t, v); } dijkstra(); for (register int i=1;i<=nodenum;putchar(' '),i++) { putnum<int>(dis[i]); } return 0; }
顺便附上一道dijkstra的题
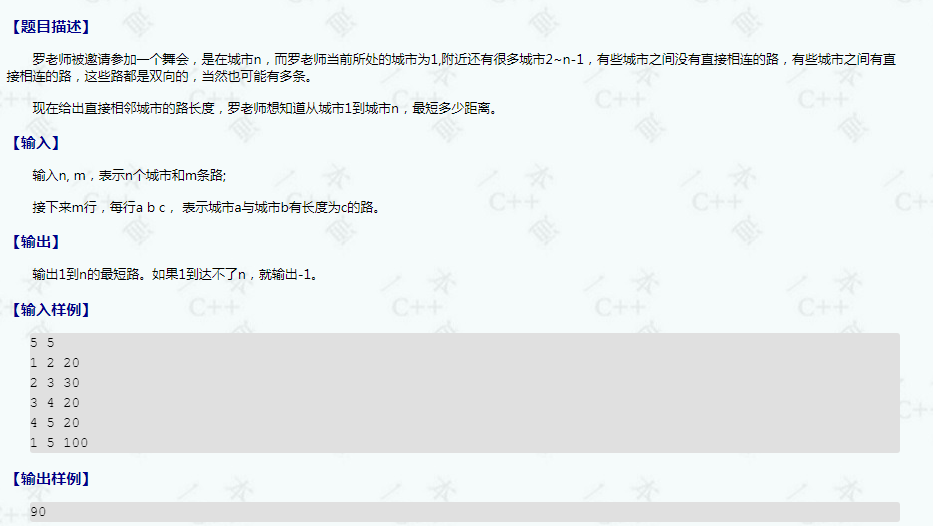
这个好像就是个模板哈
(代码from题解)
#include<iostream> #include<cstdio> #include<cstring> #include<cmath> #include<algorithm> #include<string> #include<cstdlib> #include<queue> #include<set> #include<vector> #define INF 0x3f3f3f3f #define PI acos(-1.0) #define N 3001 #define MOD 123 #define E 1e-6 using namespace std; struct node{ int pre; int next; int w; }a[N*10]; int n,m; int cnt; int head[N],vis[N],f[N]; void add(int x,int y,int w) { cnt++; a[cnt].pre=y; a[cnt].next=head[x]; a[cnt].w=w; head[x]=cnt; cnt++; a[cnt].pre=x; a[cnt].next=head[y]; a[cnt].w=w; head[y]=cnt; }//存图 int main() { cin>>n>>m; for(int i=1;i<=m;i++) { int x,y,w; cin>>x>>y>>w; add(x,y,w); } memset(f,INF,sizeof(f)); f[1]=0; vis[1]=1; int x=head[1];//手动模拟第一次出队 while(x!=0) { int y=a[x].pre; if(f[y]>a[x].w) f[y]=a[x].w; x=a[x].next; } int cnt=0; while(cnt<n)//遍历所有的点 { cnt++; int k; int minn=INF; for(int i=1;i<=n;i++) if(vis[i]==0&&f[i]<minn) { minn=f[i]; k=i; }//先把能赋值的距离赋值上 vis[k]=1; int x=head[k];//手动模拟for循环 while(x!=0)//这里木有队列,所以要while循环一次处理完 { int y=a[x].pre; int w=a[x].w; if(vis[y]==0&&f[y]>f[k]+w) f[y]=f[k]+w; x=a[x].next; } } if(f[n]==INF) cout<<"-1"<<endl; else cout<<f[n]<<endl; return 0; }
堆优化
我们上面说到dij是先挑距离起点最近的一个点b搞,然后再找距离b最近的点搞,那么每次判断距离就有点麻烦。我们换成每次挑距离起点最近的点搞,这样我们可以用堆(priority_queue)来维护距离起点最近的那个点,时间复杂度O(nmlogn)
代码:
#include<bits/stdc++.h> #define pa pair<int,int> using namespace std; inline int read() { char ch=getchar(); int x=0;bool f=0; while(ch<'0'||ch>'9') { if(ch=='-')f=1; ch=getchar(); } while(ch>='0'&&ch<='9') { x=(x<<3)+(x<<1)+(ch^48); ch=getchar(); } return f?-x:x; } int n,m,dis[100009],cnt,head[100009],s; struct Ed{ int to,dis,nxt; }edge[200009]; inline void add(int fr,int to,int dis) { cnt++; edge[cnt].to=to; edge[cnt].dis=dis; edge[cnt].nxt=head[fr]; head[fr]=cnt; } priority_queue<pa,vector<pa>,greater<pa> > q;//大根堆转小根堆 bool vis[100009]; inline void dij(int s) { for(int i=1;i<=n;i++) dis[i]=2147483645; dis[s]=0; q.push(make_pair(0,s)); while(!q.empty()) { int now=q.top().second; q.pop(); if(vis[now])continue; vis[now]=1; for(int e=head[now];e;e=edge[e].nxt) { int v=edge[e].to; if(dis[now]+edge[e].dis<dis[v]) { dis[v]=dis[now]+edge[e].dis; q.push(make_pair(dis[v],v)); } } } } int main() { n=read();m=read();s=read(); for(int i=1;i<=m;i++) { int u=read(),v=read(),w=read(); add(u,v,w); } dij(s); for(int i=1;i<=n;i++) printf("%d ",dis[i]); }