dalao曰:图论千万步,放弃第一步
存储:
1.邻接矩阵

缺点:1.有重边时很麻烦
2.空间复杂度太高
优点:写起来简单(当然还有其他优点辣)
#include <bits/stdc++.h> using namespace std; const int N = 5005; int ideg[N], odeg[N], n, m, edg[N][N]; bool visited[N]; void travel(int u, int distance) { cout << u << " " << distance << endl; visited[u] = true; for (int v = 1; v <= n; v++) if (edg[u][v] != -1 && !visited[v]) travel(v, distance + edg[u][v]); //if there is an edge (u, v) and v has not been visited, then travel(v) } int main() { cin >> n >> m; memset(edg, -1, sizeof edg); memset(visited, false, sizeof visited); for (int u, v, w, i = 1; i <= m; i++) cin >> u >> v >> w, edg[u][v] = w, odeg[u]++, ideg[v]++;//加出度和入度 for (int i = 1; i <= n; i++) cout << ideg[i] << " " << odeg[i] << endl; for (int i = 1; i <= n; i++) if (!visited[i]) travel(i, 0); }
2.邻接表
我们发现邻接矩阵中有好多位置是空的,所以我们可以只记录一个点的出边,就形成了邻接表
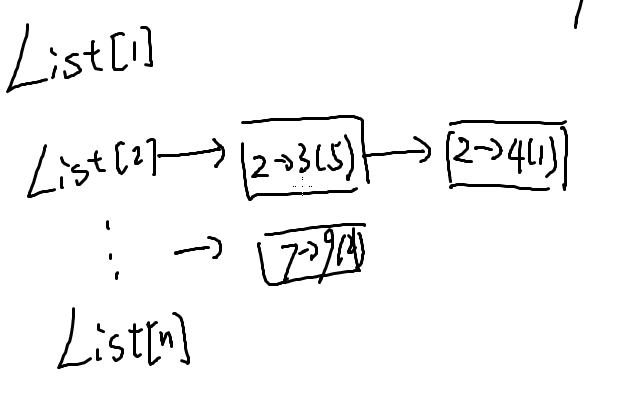 类似一个链表的形式,遍历时,只要把list[i]后面的链遍历就行了。
类似一个链表的形式,遍历时,只要把list[i]后面的链遍历就行了。
指针版本
#include <bits/stdc++.h> using namespace std; const int N = 5005; struct edge { int u, v, w; edge *next; edge(int _u, int _v, int _w, edge *_next): u(_u), v(_v), w(_w), next(_next) {} }; edge *head[N]; //List[u] stores all edges start from u int ideg[N], odeg[N], n, m; bool visited[N]; void add(int u, int v, int w) { edge *e = new edge(u, v, w, head[u]); head[u] = e; } void travel(int u, int distance) { cout << u << " " << distance << endl; visited[u] = true; for (edge *e = head[u]; e ; e = e -> next) if (!visited[e -> v]) travel(e -> v, distance + e -> w); //if there is an edge (u, v) and v has not been visited, then travel(v) } int main() { cin >> n >> m; memset(visited, false, sizeof visited); memset(head, 0, sizeof head); for (int u, v, w, i = 1; i <= m; i++) cin >> u >> v >> w, add(u, v, w), odeg[u]++, ideg[v]++; for (int i = 1; i <= n; i++) cout << ideg[i] << " " << odeg[i] << endl; for (int i = 1; i <= n; i++) if (!visited[i]) travel(i, 0); }
来我们看看好理解的数组版本
#include <bits/stdc++.h> using namespace std; const int N = 5005; struct edge { int u, v, w, next; }edg[N]; int head[N]; //记录每个点的最后一条出边的编号,方便记录next int ideg[N], odeg[N], n, m, cnt; //cnt: 边的编号 bool visited[N]; void add(int u, int v, int w) { int e = ++cnt;//编号加以 edg[e] = (edge){u, v, w, head[u]};//e的next是当前的head[u](u是起点) head[u] = e; } void travel(int u, int distance)//遍历 { cout << u << " " << distance << endl; visited[u] = true; for (int e = head[u]; e ; e = edg[e].next)//终止条件:next不存在 if (!visited[edg[e].v]) travel(edg[e].v, distance + edg[e].w); //如果没有遍历过,就遍历它 } int main() { cin >> n >> m; cnt = 0; memset(visited, false, sizeof visited); memset(head, 0, sizeof head); for (int u, v, w, i = 1; i <= m; i++) cin >> u >> v >> w, add(u, v, w), odeg[u]++, ideg[v]++; for (int i = 1; i <= n; i++) cout << ideg[i] << " " << odeg[i] << endl; for (int i = 1; i <= n; i++) if (!visited[i]) travel(i, 0); }
举个例子
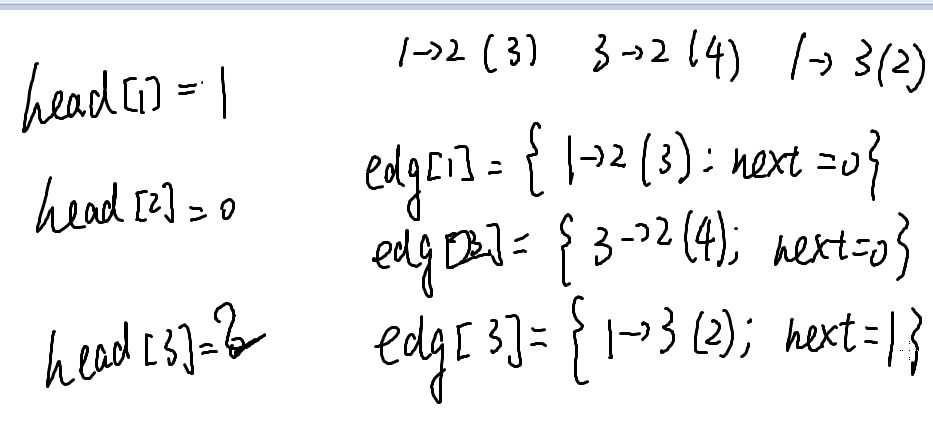
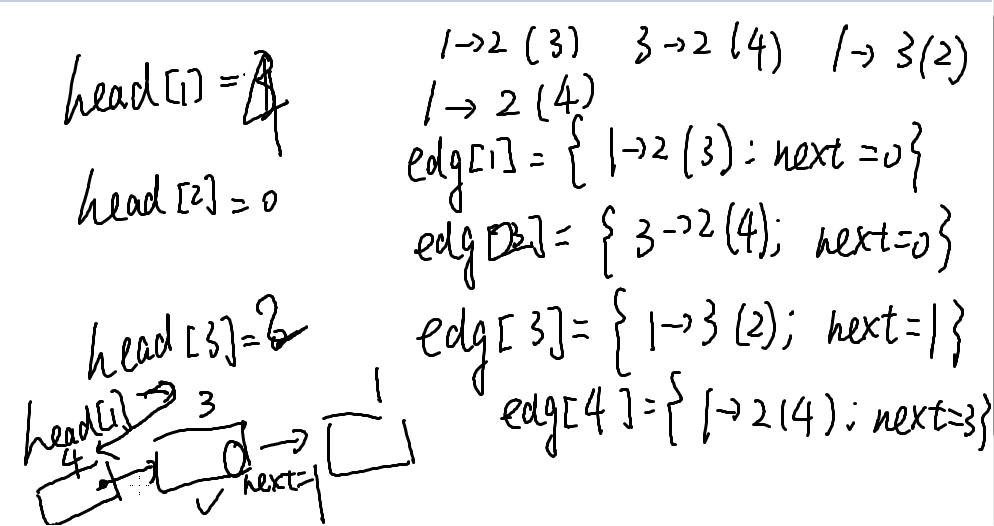
二维数组模拟邻接表
edg[u][k]记录从u出发的第k条边,不过还是n^2的。因为在一开始,我们就确定了数组的长度,所以还是有浪费。
怎么办?vector。

vector是用多少,有多少(变长数组)
#include <bits/stdc++.h> using namespace std; const int N = 5005; struct edge { int u, v, w; }; vector<edge> edg[N]; //长度为n,每个元素是vector的东西(变长数组)这里edg[0]是边长数组,edg[1]也是变长数组.....以此类推 int ideg[N], odeg[N], n, m, cnt; //cnt: numbers of edges bool visited[N]; void add(int u, int v, int w) { edg[u].push_back((edge){u, v, w}); } void travel(int u, int distance)//distance:当前的路径总长度 { cout << u << " " << distance << endl; visited[u] = true; for (int e = 0; e < edg[u].size(); e++)//访问u的所有出边:上限:u的出边数量 if (!visited[edg[u][e].v])//edg[u][e]:以u出发的第e条出边 travel(edg[u][e].v, distance + edg[u][e].w); //如果没有遍历过,就遍历 } int main() { cin >> n >> m; cnt = 0; memset(visited, false, sizeof visited); for (int u, v, w, i = 1; i <= m; i++) cin >> u >> v >> w, add(u, v, w), odeg[u]++, ideg[v]++;//记录入度,出度 for (int i = 1; i <= n; i++) cout << ideg[i] << " " << odeg[i] << endl; for (int i = 1; i <= n; i++) if (!visited[i]) travel(i, 0); }
dalao 曰:代码比开机要简单
生成树:

就是从一个无向连通图中,选一个子图,使这个子图构成一棵树。这个子图就是生成树
树:无环
举个简单的例子
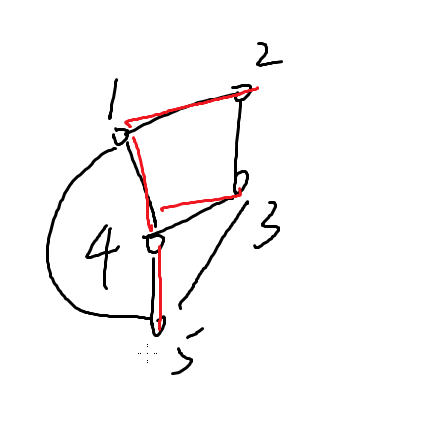
红色部分就是生成树
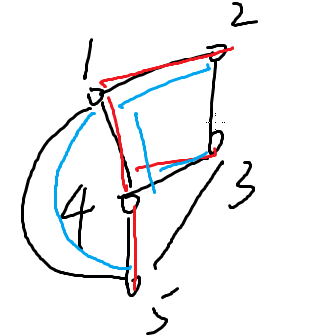
蓝色也是生成树
一个图的生成树的数量是指数级别的
瓶颈生成树

就是求所有边中,最大的边权最小的那棵生成树
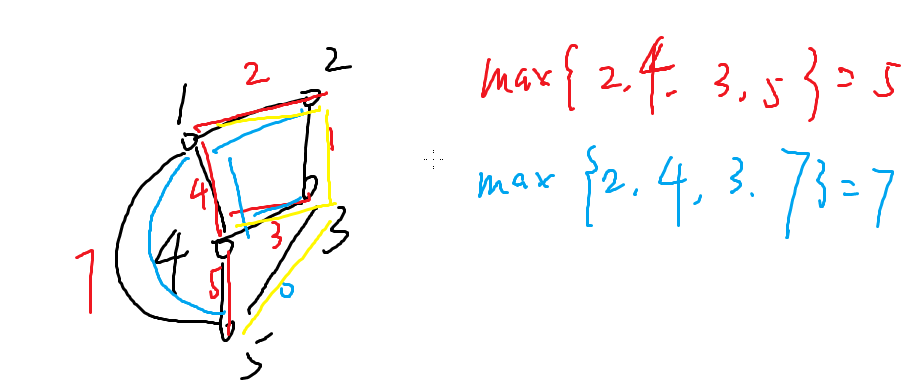
这里红色比蓝色更优
和最小生成树的区别:


求瓶颈生成树,不需要全部学这些算法
直接讲kruskal

判断联通:并查集。
重复过程直到加入了n-1条边
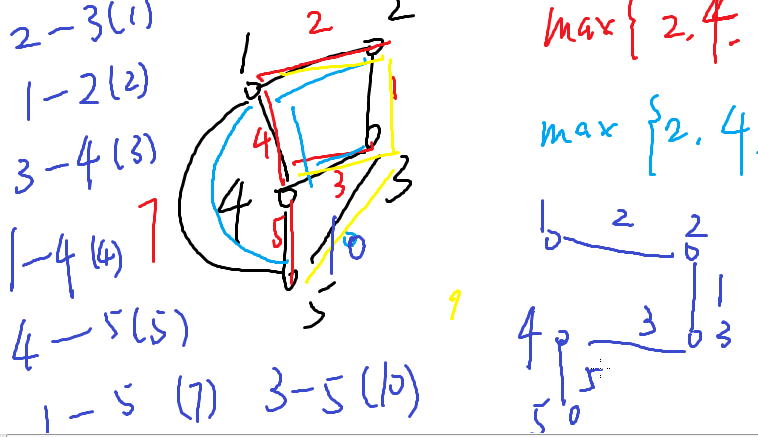
为什么是对的?
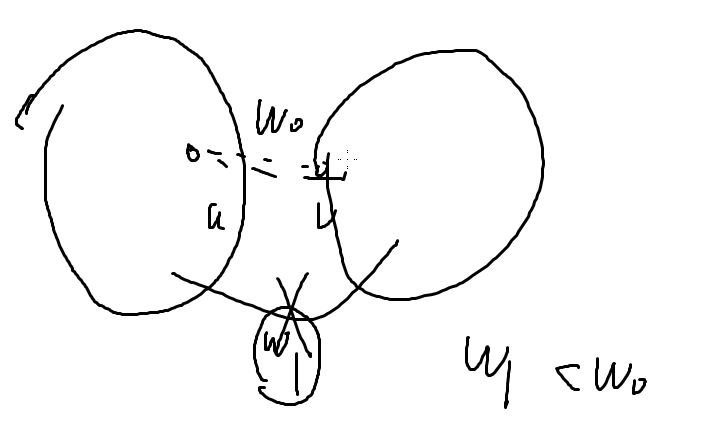
最开始u,v在不同的两个联通块里,现在有一条边w0,但到最后肯定会处于同一个联通块里,所以最后两个连通块中肯定有一条边,假设最后那条边是w1,但是现在w1没有加入,按这个算法,w1一定是比w0小,所以是对的。
上面的证明并不严谨
下面是严谨的证明。
我们先讲一下闲圈算法消圈算法
把一个环的边从大到小排序。然后把大的边去掉,最后就是最小生成树。kruskal可以用消圈算法证明,不过是把消圈算法反过来。不是去掉边,而是从小到大,加入边。
为什么消圈算法不行?找环太麻烦了。
dalao曰:手速不行就去多玩点游戏,比如扫雷什么的
代码:
#include <bits/stdc++.h> using namespace std; const int maxn = 1000005; struct edge { int u, v, w; }edg[maxn]; int n, m, p[maxn], ans = 0; bool cmp(edge a, edge b) {return a.w < b.w;} int findp(int t) {return p[t] ? p[t] = findp(p[t]) : t;} bool merge(int u, int v) { u = findp(u); v = findp(v); if (u == v) return false; p[u] = v; return true; } int main() { cin >> n >> m; for (int i = 1, u, v, w; i <= m; i++) cin >> u >> v >> w, edg[i] = (edge){u, v, w}; sort(edg + 1, edg + m + 1, cmp);//排序 for (int i = 1; i <= m; i++) if (merge(edg[i].u, edg[i].v))//将两个点放进同一个连通块里 ans = max(ans, edg[i]. w); cout << ans << endl; }
路径:
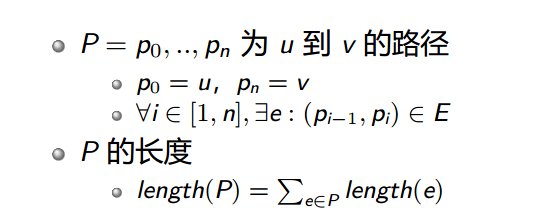
举个例子:
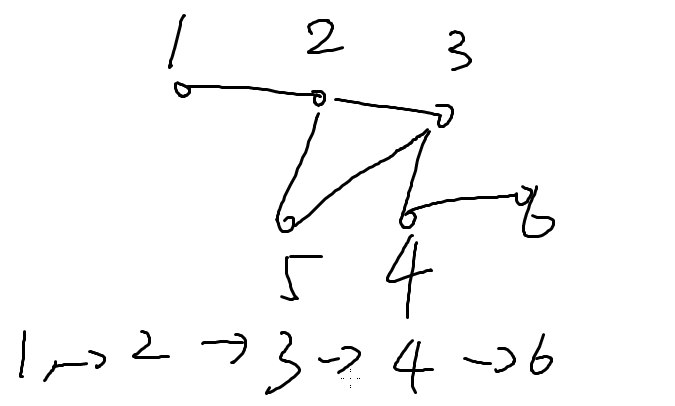
上面就是从1到6的路径
但是路径可以有多条。
简单路径:不经过重复的点
路径长度:路径上所有边的边权之和
最短路径问题:

每个都要掌握 qwq,当然spfa是bellman_ford的一个优化
![]()
即 (松弛过后)
(松弛过后)
其实就是一个取min的操作,所有求最短路径的算法都是这个思想。
floyd:

似乎就是个DP qwq
这里我们举个例子
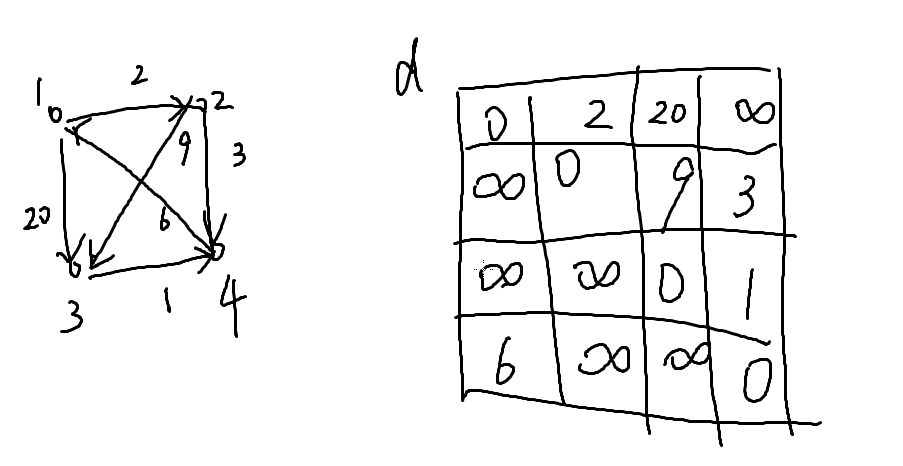
k=1:d[4][2]=d[4][1]+d[1][2]=8,d[4][3]=d[4][1]+d[1][3]=26
k=2:可以更新:d[1][4]=2+3=5,d[1][3]=d[1][2]+d[2][3]=11,
k=3:什么都做不了
k=4:d[3][1]=d[3][4]+d[4][1]=7,d[2][1]=d[2][4]+d[4][1]=9
证明:
举个例子
设![]() 是3到5的最短路径,那么4到7的最短路径一定是4->1->7.在k=1时,d[4][7]成为真实值。
是3到5的最短路径,那么4到7的最短路径一定是4->1->7.在k=1时,d[4][7]成为真实值。
k=2:d[3][4]完成
k=3:无影响
k=4:d[3][7]完成(d[3][4]正确,且d[4][7]z正确)
k=5,6:无影响
k=7:d[3][5]完成
在任意一个图里,不断枚举k,就不断完成一些点的真实值。最后全部完成
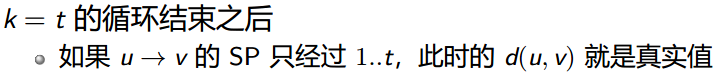
思想:不断枚举中间点
代码:
#include<iostream> #include<cstdio> #include<cmath> #include<cstring> #include<algorithm> using namespace std; int n,d[101][101],m; const int inf=0x3ffff; int main() { scanf("%d%d",&n,&m); for(int i=1;i<=n;i++)//初始化 {for(int j=1;j<=n;j++) d[i][j]=inf; d[i][i]=0; } for(int i=1;i<=m;i++) {int x,y,z; scanf("%d%d%d",&x,&y,&z); d[x][y]=min(d[x][y],z);//无向图的话就是d[y][x]=d[x]y] } for(int k=1;k<=n;k++)//注意枚举顺序 {for(int i=1;i<=n;i++) {for(int j=1;j<=n;j++) {d[i][j]=min(d[i][j],d[i][k]+d[k][j]); if(d[i][j]<0)//注意负权环 {printf("有负权环!");return 0; } } } } for(int i=1;i<=n;i++) for(int j=1;j<=n;j++) printf("d[%d][%d]=%d ",i,j,d[i][j]); }
复杂度:O(n^3) (最多跑n=500)
优势:全部跑完一遍之后,任意两点最短路O(1)询问
有什么问题?
有负权环:

这样会用floyd一直怼,最后炸了。所以也可以用floyd检查是否有负权环。(d[u][u]<0)
当然大部分数据不会有负权环的。
Bellman-ford
单源最短路:



其实n-1次就够了
复杂度:O(nm)
依旧是可以判负权环

因为在n-1次时,所有值是真实值,但如果有负权环,就会被更新(有负权边不会改变)
代码:
#include<iostream> #include<cstdio> #include<algorithm> using namespce std; int head[10001],cnt,dis[10001]; struct Edge{ int to,dis,next; }edge[500001]; void add(int fr,int to,int dis) { edge[++cnt].to=to; edge[cnt].dis=dis; edge[cnt].next=head[fr]; head[fr]=cnt; }//上面都是存图 int main() { int s; scanf("%d%d%d",&n,&m,&s); for(int i=1;i<=m;i++) {int fr,to,dis; scanf("%d%d%d",&fr,&to,&dis); add(fr,to,dis); } for(int i=1;i<=n;i++)dis[i]=inf; dis[s]=0; for(int i=1;i<=n;i++)//循环n边(每个点来一遍) { for(int j=head[i];j;j=edge[j].next)//链式前向星遍历 { int v=edge[j].to,d=edge[j].dis;//这里就是上面的式子 dis[v]=min(dis[v],dis[i]+d); } } for(int i=1;i<=n;i++) printf("%d ",dis[i]); }
spfa:
对bellman_ford的优化
在bellman-ford中,我们是对全部边进行松弛操作。
但是对于一个u,在上一轮去全局松弛中,没有被更新,那么这一轮就没有必要考虑u的出边。因为只有d[u]才会影响到所有的v,v为u的出边的终点的d[v]。如果d[u]没变,后面就没有必要了。
所以我们维护一个队列,记录d[u]被改变的u,然后枚举u所有出边e,进行松弛,将u出队。对于每一个u的终点v,如果d[v]>d[u]+w,就更新d[v],再将v入队。注意这里一个v可以多次入队。
终止:队空 / d[u]进队列n-1次以上。如果u入队n-1次以上,那就有负权环。
复杂度:O(km)(最坏情况:O(nm))(k的期望为2,但是看数据喽,毒瘤数据也是nm,k为每个点被更新的次数)(记住spfa是会退化的)
网格图可以卡掉spfa
就像这种,每个点是一个交点,就是网格图。
在判断网格图时,可以跑一边spfa,如果炒鸡慢,一般就是网格图
代码:
#include <bits/stdc++.h> using namespace std; const int N = 1e5 + 5; const int inf = 1 << 29; struct edge{ int u, v, w; }; vector<edge> edg[N]; int d[N], n, m, S; queue<int> Queue; bool inQueue[N]; int cntQueue[N]; void add(int u, int v, int w) { edg[u].push_back((edge){u, v, w}); } int main() { cin >> n >> m >> S; for (int i = 1; i <= n; i++) d[i] = inf; for (int u, v, w, i = 1; i <= m; i++) cin >> u >> v >> w, add(u, v, w); d[S] = 0; inQueue[S] = true; Queue.push(S);//将原点入队 while (!Queue.empty()) { int u = Queue.front(); Queue.pop(); inQueue[u] = false;//出队后,u就不在队列里了 for (int e = 0; e < edg[u].size(); e++) { int v = edg[u][e].v, w = edg[u][e].w; if (d[v] > d[u] + w)//可以更新 { d[v] = d[u] + w;//更新 if (!inQueue[v])//再判是否入队 { Queue.push(v); ++cntQueue[v]; inQueue[v] = true;//注意先入队,再记录入队次数 if (cntQueue[v] >= n) {cout << "Negative Ring" << endl; return 0;}//如果有负权环,就结束 } } } } for (int i = 1; i <= n; i++) cout << d[i] << endl; }
dijkstra
适用:无负权边(比如走高速公路什么的)

从起点出发,松弛所有直达点,找到距离起点最近的一个直达点,由它再松弛它的直达点,再找到一个距离它最近的直达点,继续松弛............
所以我们维护一个队列,队列里的点已经被松弛过,找到一个不在队列中,d最小的点u,松弛所有出边,并将u入队
例子:
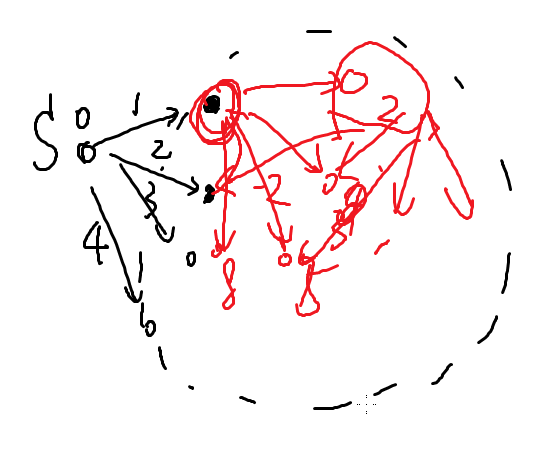
在上图中,先松弛起点的直达点,然后找到了圈红圈的点,再由这个点进行松弛操作。
证明:显然易证
因为在队列中的点的d已经是真实值了
如何判断点是否在队列里?一次O(N)暴力扫描
int head[10001],dis[100001],cnt; bool dl[10001]; struct Edge{ int to,dis,next; }edge[500001]; void add(int fr,int to,int dis) { edge[++cnt].dis=dis; edge[cnt].to=to; edge[cnt].next=head[fr]; head[fr]=cnt; } int main() { scanf("%d%d",&n,&m); for(int i=1;i<=m;i++) {int x,y,z; scanf("%d%d%d",&x,&y,&z); add(x,y,z); } //dijkstra(辣鸡版本): for(int i=1;i<=n;i++) {int u; for(int j=1;j<=n;j++) if(!dl[j]&&d[j]<d[u])u=j; for(int i=head[u];i;i=edge[i].next) { dis[edge[i].to]=min(dis[edge[i].to],dis[u]+edge[i].dis); } } }
复杂度:O(n^2+m)
优化:小根堆
显然它太慢了
我们可以维护一个小根堆,里面记录没有被用来更新的点u的d,每次取最上面的。如果d[v]被更新了,就把新的d[v]放进堆里,原来的d[v]一定比现在的d[v]大,那么原来的d[v]会在现在的d[v]之后出堆,如果我们发现一个点的所有出边的终点已经被松弛过了,就不需要管他了。所以原来的d[v]就不用管了。
堆这种东西,就是优先队列辣qwq

代码
#include <bits/stdc++.h> using namespace std; const int N = 1e5 + 5; const int inf = 1 << 29; struct edge{ int u, v, w; }; vector<edge> edg[N]; int d[N], n, m, S; bool relaxed[N]; struct Qnode { int u, du; bool operator<(const Qnode &v) const {return v.du < du;} }; priority_queue<Qnode> PQueue; void add(int u, int v, int w) { edg[u].push_back((edge){u, v, w}); } int main() { cin >> n >> m >> S; for (int i = 1; i <= n; i++) d[i] = inf; for (int u, v, w, i = 1; i <= m; i++) cin >> u >> v >> w, add(u, v, w); d[S] = 0; PQueue.push((Qnode){S, 0}); while (!PQueue.empty()) { int u = PQueue.top().u; PQueue.pop(); if (relaxed[u]) continue; //if edges staring from u are already relaxed, no need to relax again. relaxed[u] = true; for (int e = 0; e < edg[u].size(); e++) { int v = edg[u][e].v, w = edg[u][e].w; if (d[v] > d[u] + w) { d[v] = d[u] + w; PQueue.push((Qnode){v, d[v]}); //if d(v) is updated, push v into PQueue } } } for (int i = 1; i <= n; i++) cout << d[i] << endl; }
先将个东西
DAG

弱连通:把有向图改为无向图后连通。
拓扑排序:

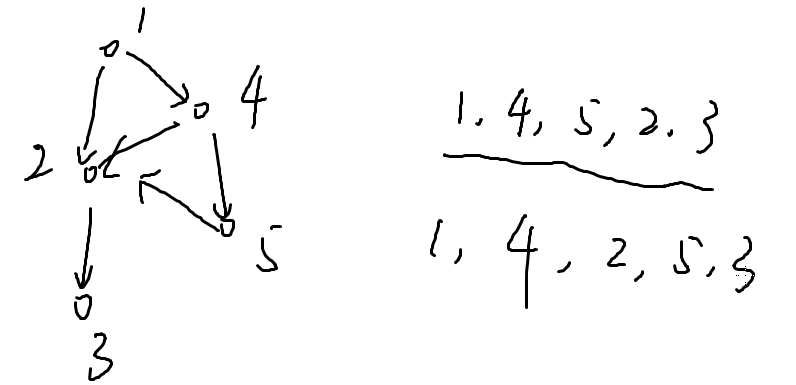
第一个:true
第二个:false
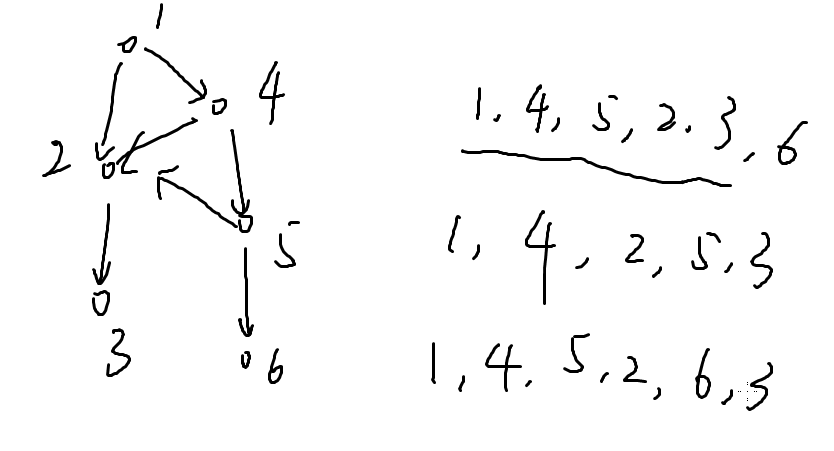
再加一个点:拓扑序有很多(阶乘级别)
直观上好像并不那么显然,我们依旧用上个图举例
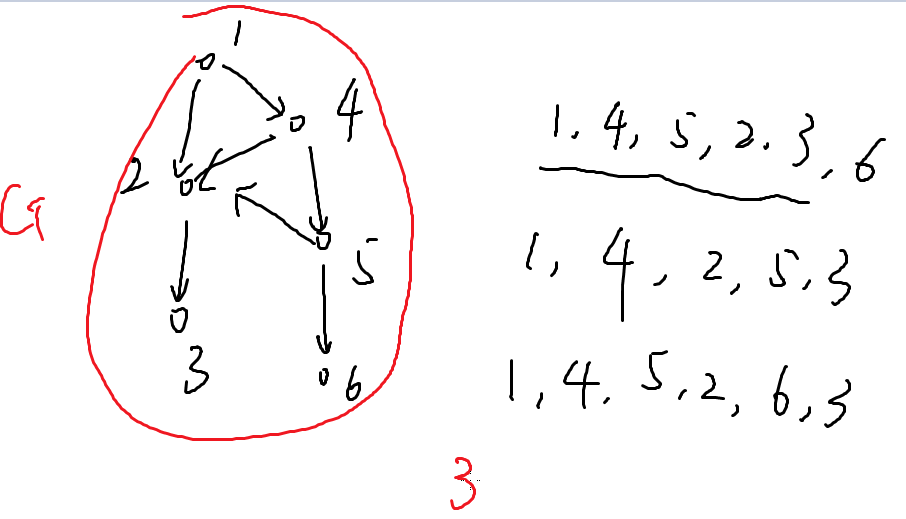
出度为0:3,6
把指向3的边扔掉,在拓扑序的最后写下3
之后再找,再写(从后往前找)。
1 4 5 6 2 3
任何一个DAG都有拓扑序:
任意一个DAG一定有出度为0的点,如果没有,就踏遍了天南地北。(因为DAG一共有n个点,但是没有的话,还可以继续走下去,然后就有环了)
删掉一个点,肯定还是个DAG,肯定还有出度为0的点,继续找继续找继续找......拓扑序出来了

#include <bits/stdc++.h> using namespace std; const int N = 1e5 + 5; const int inf = 1 << 29; struct edge{ int u, v; }; vector<edge> edg[N]; int n, m, outdeg[N], ans[N]; queue<int> Queue; void add(int u, int v) { edg[u].push_back((edge){u, v}); } int main() { cin >> n >> m; for (int u, v, i = 1; i <= m; i++) cin >> u >> v, add(v, u), outdeg[u]++;//因为邻接表记录的是出边,所以这里反过来记 for (int i = 1; i <= n; i++) if (outdeg[i] == 0) Queue.push(i); for (int i = 1; i <= n; i++) { if (Queue.empty()) {printf("Not DAG"); return 0;} int u = Queue.front(); Queue.pop(); ans[n - i + 1] = u; for (int e = 0; e < edg[u].size(); e++) { int v = edg[u][e].v;//取一个点,把它的出边终点的出度都减少1 if (--outdeg[v] == 0) Queue.push(v);//出度为0:加入拓扑序 } } }
拓扑排序的用处:
1.求单源最短路:
拓扑序中,出现在原点前面的是无穷
LCA:

有q组询问,在o(logn)的时间内完成一组询问
O(n):先条到同一深度,在同时往上跳。
O(log n):树上倍增

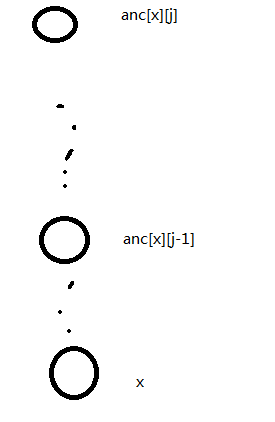
一个比较直观的图

如此魔幻的括号,懂了就不要看了,伤眼。

举个例子
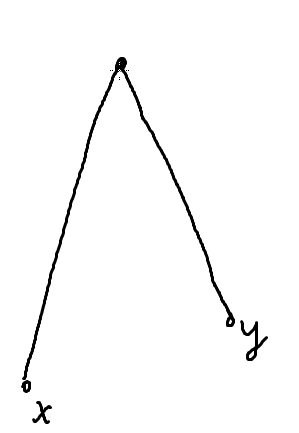
这是个很长的路径,不是一条边
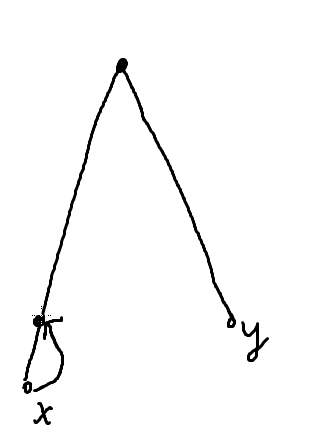
跳到同一深度
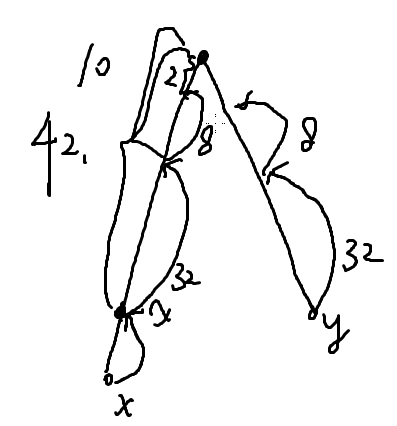
跳的深度从log 2 n开始,到1
如果跳了之后相遇,就不跳,不然就跳,跳完后再往上一个就是答案



因为x-->t=len(x)-len(t)


MST:最小生成树(不是瓶颈生成树)
但这里指的是瓶颈生成树
为什么?
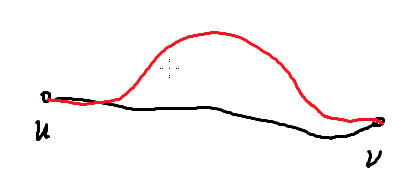
红色是瓶颈生成树的路径。
看起来好像有环的样子。
如果黑色的是答案路径的话,说明黑色上的最大边权,比红色的最大边权要小,而且在有环的情况下.....wait!好像哪里不对的样子,所以这是矛盾的,所以答案就不可能在黑色上面。

最后一句是个什么鬼呢?
简单举个例子:
x到它的64层祖先的最大值=max(x到32层祖先的最大值,x的32层祖先到x的64层祖先的最大值)
就是这样(这里叫倍增)
简单说一下倍增和分治的区别:
分治:把一个大问题分解为几个不重叠的小问题,解决完小问题之后合并。
倍增:先预处理出最底层问题的解,再按某种倍数关系合并。
代码:显然这个题很难,不用证明,所以——————咕咕咕