线段树2（P3373）

传送

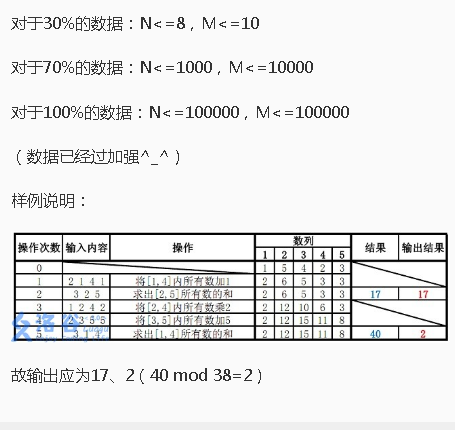
感谢洛谷题解让我理清了这一撮标记

这里多了一个乘法操作，乘法的优先级高于加法。我们来思考一下有关标记的问题。

首先由两种操作，可以想到要有两个标记，一个标记乘法(mul[k])，一个标记加法(add[k])。

如果这一步是加法，就直接在原来的add上面增加即可(加法不会对mul产生影响)(这里的“原来的add”是指已经处理好加法，乘法关系的add)，sum也按照线段树1的方式维护。

如果这一步是乘法，因为乘法的优先级高于加法，所以乘法会对当前的add产生影响，即add[k]要乘当前的数。mul[k],sum[k]直接乘当前的数即可。

再考虑一下标记下传。

子节点收到父亲节点的add和mul之后，我们就要考虑是先用父亲的add还是mul去更新子节点（即先乘再加还是先加再乘）。我们上面处理add的时候，就已经考虑到了mul对add的影响，如果这时候先加再乘，就会造成翻倍的错误，所以我们先乘再加（也就是先让子节点的add乘父节点的mul,再加上父节点的add）。sum[子节点]要先乘mul[父节点],再加上add[父节点]*(r-l+1)。

理清了两种标记之间的关系，剩下的就是线段树板子了。这里要注意建树的时候，mul[k]初始值为1，add[k]初始值为0。

代码：

#include<bits/stdc++.h>
#define ll long long
using namespace std;
const ll N=100009;
ll n,m,p;
ll val[N*4],sum[N*4],add[N*4],mul[N*4];
ll read()
{
    char ch=getchar();
    ll x=0;bool f=0;
    while(ch<'0'||ch>'9')
    {
        if(ch=='-')f=1;
        ch=getchar();
    }
    while(ch>='0'&&ch<='9')
    {
        x=(x<<3)+(x<<1)+(ch^48);
        ch=getchar();
    }
    if(f)x=-x;
    return x;
}
void build(ll k,ll l,ll r)
{
    mul[k]=1;
    if(l==r)
    {
        sum[k]=val[r];    
        return ;
    }
    ll mid=(l+r)>>1;
    build(k<<1,l,mid);
    build(k<<1|1,mid+1,r);
    sum[k]=(sum[k<<1]+sum[k<<1|1]+p)%p;
    return;
}
void change(ll k,ll l,ll r,ll u)
{
        add[k]=(mul[u]*add[k]%p+add[u])%p;//记得随时%p
    mul[k]=(mul[k]*mul[u])%p;
    sum[k]=(sum[k]*mul[u]%p+add[u]*(r-l+1)%p)%p;
}
void pushdown(ll k,ll l,ll r)//标记下传
{
    ll mid=(l+r)>>1;
    change(k<<1,l,mid,k);
    change(k<<1|1,mid+1,r,k);
    add[k]=0;
    mul[k]=1;
    return;
}
void Mul(ll k,ll l,ll r,ll x,ll y,ll v)
{
    if(l>=x&&r<=y)
    {
        mul[k]=(mul[k]*v)%p;
        add[k]=(add[k]*v)%p;
        sum[k]=(sum[k]*v)%p;
        return ;
    }
    pushdown(k,l,r);
    ll mid=(l+r)>>1;
    if(x<=mid)
      Mul(k<<1,l,mid,x,y,v);
    if(mid<y)  
      Mul(k<<1|1,mid+1,r,x,y,v);
    sum[k]=(sum[k<<1]+sum[k<<1|1]+p)%p;
    return;  
}
void Add(ll k,ll l,ll r,ll x,ll y,ll v)
{
    if(l>=x&&r<=y)
    {
        add[k]=add[k]+v;
        sum[k]=(sum[k]+v*(r-l+1)%p)%p;    
        return ;
    }

    pushdown(k,l,r);
    ll mid=(l+r)>>1;
    if(x<=mid)
      Add(k<<1,l,mid,x,y,v);
    if(mid<y)
      Add(k<<1|1,mid+1,r,x,y,v);
    sum[k]=(sum[k<<1]+sum[k<<1|1]+p)%p;
    return ;        
}
ll query(ll k,ll l,ll r,ll x,ll y)
{
    if(l>=x&&r<=y)
        return sum[k]%p;
    pushdown(k,l,r);
    ll mid=(l+r)>>1;
    ll ans=0;
    if(x<=mid)
      ans+=query(k<<1,l,mid,x,y);
    if(mid<y)
      ans+=query(k<<1|1,mid+1,r,x,y);
    return (ans+p)%p;    //防止出现负数
}
int main()
{
    n=read();m=read();p=read();
    for(int i=1;i<=n;i++)
      val[i]=read()%p;
    build(1,1,n);
    for(int i=1;i<=N*4;i++)
     mul[i]=1;
    for(int i=1;i<=m;i++)
    {
        ll cz,x,y;
        cz=read();x=read();y=read();
        if(cz==1)
        {
            ll k=read();
            Mul(1,1,n,x,y,k);
        }
        if(cz==2)
        {
            ll k=read();
            Add(1,1,n,x,y,k);
        }
        if(cz==3)
        {
            printf("%lld
",query(1,1,n,x,y));
        }
    }  
}