

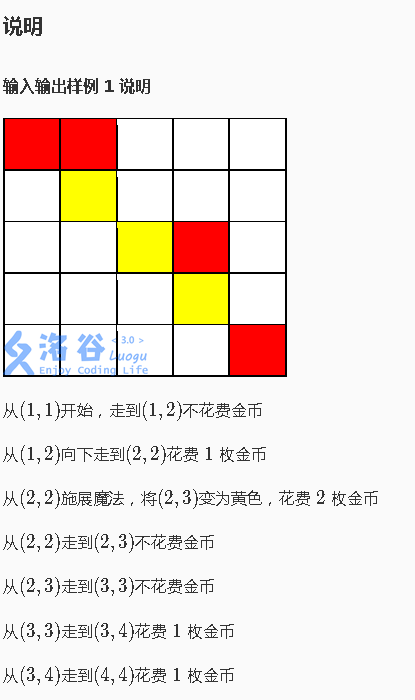



这看起来有点像个搜索,那我们就用搜索试试。
dfs?bfs?
其实都可以,但是窝只会dfs.。
既然这里要用dfs,那么就要把每次搜到(m,m)时,使用的金币数量进行比较,取最小值。
在搜索过程中肯定会遇到很多不是最优解的情况。既然不是最优解,那么我们可以用某些方式在搜索过程中就把这些情况给剪掉。(也就是剪枝)我们不妨再开一个二维数组best,best[i][j]表示走到点(i,j)所用的最少金币数量。这样搜索到点(i,j)时,如果当前花费的金币总数不小于best[i][j],那么就算这种情况能够到达终点,它也一定不是最优解,所以我们直接返回,不再搜索。这样就可以节省很多的时间(至少不会TLE)
再考虑一些细节
这里我们就不判断每个点是否到过了,因为在上面的剪枝中,第二次到达一个搜索过的点,花费的金币肯定不比第一次到达时花费的少。
在搜索时,我们只搜索有颜色的点。对于那些可以使用魔法的无色格子,我们就直接把它设成有颜色的,并且标记已经使用过魔法。在回溯的时候再使它的颜色变为无色就好。
这里红色是0,黄色是1,而那些没有颜色的点的初始值也是0。所以我们在输入颜色的时候,将有颜色的点的颜色+1,就可以区分了。
代码:
#include<bits/stdc++.h> using namespace std; int m,n,ma[109][109],be[109][109];//be就是best,ma就是map(地图) int dx[4]={1,-1,0,0},dy[4]={0,0,1,-1}; int read()//快读 { char ch=getchar(); int x=0;bool f=0; while(ch<'0'||ch>'9') { if(ch=='-')f=1; ch=getchar(); } while(ch>='0'&&ch<='9') { x=(x<<3)+(x<<1)+(ch^48); ch=getchar(); } f?x=-x:x=x; return x; } void dfs(int nowx,int nowy,int cost,bool magic) { if(nowx==m&&nowy==m) { be[m][m]=min(be[m][m],cost); return ; } if(cost>=be[nowx][nowy])return ; be[nowx][nowy]=cost; for(int i=0;i<=3;i++) { int ex=nowx+dx[i],ey=nowy+dy[i]; if(ex>=1&&ex<=m&&ey>=1&&ey<=m) { if(ma[ex][ey]!=0)//只搜索有颜色的点(无色可以覆盖成有色) { if(ma[ex][ey]==ma[nowx][nowy]) dfs(ex,ey,cost,0); else dfs(ex,ey,cost+1,0); } else if(magic==0)//对于无色的点,看是否能使用魔法 { ma[ex][ey]=ma[nowx][nowy]; dfs(ex,ey,cost+2,1); ma[ex][ey]=0;//一定要记得回溯啊 } } } } int main() { m=read();n=read(); for(int i=1;i<=n;i++) { int x=read(),y=read(),c=read(); c++; ma[x][y]=c; } memset(be,63,sizeof(be)); dfs(1,1,0,0); if(be[m][m]<1061109567)//memset之后be的值是1061109567 printf("%d ",be[m][m]);//be[m][m]就是最后的解 else printf("-1"); return 0; }