在放板子的代码之前,先讲一下树状数组。
树状数组的作用:
在有修改时可以做到log级别求前缀和
还可以结合差分等神奇的东西食用
空间比线段树要省的多,代码量也少的多
在单点查询的时候比线段树快了不是一点(我真的没有拿线段树的板子去拍这两个题)
我们先来看一下树状数组是个什么东西
首先,我们有一个序列A,其次lowbit(x)表示x的二进制表示中,最低位的1和后面的0构成的数。
树状数组c[i]记录序列A的区间[i-lowbit(i)+1,x]中所有数的和。
why?我们画一画树状数组
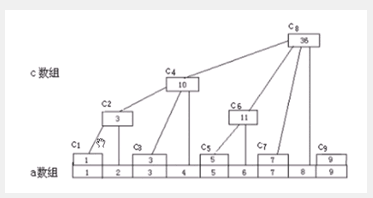
它是不是很像一棵树
同时我们可以发现一些性质:
每个c[x]保存了以它为根的子树中叶节点的和
c[x]的子节点数=lowbit(x)
c[x]的父亲是c[x+lowbit(x)]
树深度为logn
占用空间:O(n)
lowbit好像很重要的样子,so,lowbit怎么求呢
lowbit(x)=x&(~x+1)=x&-x,因为~x+1=-x。
why?
举个例子(设x>0,这里牵扯到树状数组不能处理下标为0的情况)

树状数组支持两种神奇的修改与查询。
一.单点修改,区间查询(板子1)
二.区间修改,单点查询(板子2)
先说一说第一种
前面提到过c[x]的父亲是c[x+lowbit(x)],所以更改的代码就是这样:
void update(int x,int v) { for(;x<=n;x+=x&(-x))c[x]+=v; }
因为c数组是维护的前缀和,所以当查询区间[l,r]的时候,我们可以算出sum(r)-sum(l-1),这里sum(i)是[1,i]的和。
怎么算sum(i)?
因为c[x]记录的是[lowbit(x)+1,x]这个区间的和,为了统计[1,x],所以我们每次x要减去lowbit(x)。
代码
int sum(int x) { int ans=0; for(;x>=1;x-=x&(-x))ans+=c[x]; return ans; }
再来说一说第二种神奇的操作(区间修改,单点查询)我真的没有拿线段树的板子做这道题
我们先看一个东西:差分
现在有一个a数组:a[1],a[2]……a[n]
还有一个b数组:b[1]=a[1]-a[0],b[2]=a[2]-a[1]……b[i]=a[i]-a[i-1]
b数组就叫做差分数组。
通过差分数组的定义,我们知道:a[2]=a[1]+b[2]=b[1]+b[2],a[3]=a[2]+b[3]=b[1]+b[2]+b[3]……
我们发现了差分的一个性质:a[i]=b[1]+b[2]+……+b[i]
那差分有什么用呢?
我们想到这里是区间修改,如果把区间中的每一个点当做单点修改,复杂度O(nlogn),好像还不如暴力,而且树状数组也木有懒标记之类的操作,这时就要用到差分数组了。
若我们让[l,r]这个区间每个数都加上k,则对于差分数组来说,会变的只有b[l],b[r+1]。因为a[l]加了k,而a[l-1]不变,所以b[l]增加了k,a[r]增加了k,a[r+1]不变,所以b[r+1]减少k。
当单点查询时,就是询问前缀和(也就是上面差分的性质)
so,我们只是把树状数组维护的对象从a数组变成了它的差分数组b数组而已,其他的不变。
这里放上板子
#include<bits/stdc++.h>//这个是板子2,板子1也差不多 using namespace std; int n,m,c[5000009],a[500009]; int read() { char ch=getchar(); int x=0;bool f=0; while(ch<'0'||ch>'9') { if(ch=='-')f=1; ch=getchar(); } while(ch>='0'&&ch<='9') { x=(x<<3)+(x<<1)+(ch^48); ch=getchar(); } return f?-x:x; } void update(int x,int v) { for(;x<=n;x+=x&(-x))c[x]+=v; } int sum(int x) { int ans=0; for(;x>=1;x-=x&(-x))ans+=c[x]; return ans; } int main() { n=read(); m=read(); for(int i=1;i<=n;i++) a[i]=read(); for(int i=1;i<=n;i++) update(i,a[i]-a[i-1]); //在初始化时,直接在i的位置加上a[i]-a[i-1] for(int i=1;i<=m;i++) { int cz=read(),x=read(); if(cz==1) { int y=read(),k=read(); update(x,k); update(y+1,-k); } else printf("%d ",sum(x)); } }