灵魂画师题解

可以忽略的吐槽

当窝切掉了T1签到题之后，hin开心的打开T2，然鹅醒目的期望让窝怀疑人生。

开始正文

来我们康康题目



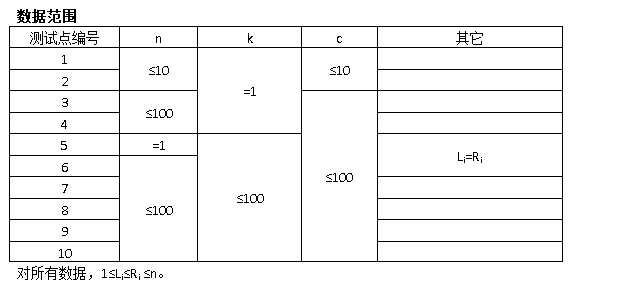
显然这题爆搜只有20。
那我们想想到底是什么让我们的爆搜炸掉了。
1.枚举子集这玩意不是一般的恶心
2.显然操作越多，n张纸颜色的状态就越多，并且(nleq100),并不能状压
第二点显然也是第一点导致的。
所以主要就是怎么搞掉这个“枚举子集”。
如果从全局来看，显然并不好弄，所以我们不妨换个视角。从某张纸的角度出发，我们可以知道包含这张纸的操作区间一共有多少个，即这张纸最多可能被选中几次。对于每一次操作，这张纸被选中的几率是(frac{1}{2})，被涂上j的几率是(frac{1}{c})。最终对决定对答案贡献是当前这张纸上的颜色，所以我们不妨设(dp[i][j])表示进行了(i)次操作，纸上的颜色是(j)的概率，最后算贡献的时候只需乘(j)即可。转移方程：如果这张纸被选中了：(dp[i][j*k)%(c]+=dp[i-1][j]/(c*2))。如果没被选中：(dp[i][j]+=dp[i-1][j]/2)(因为被选中和不被选中的几率都是 (frac{1}{2}) ,所以都要乘 (frac{1}{2}) )。那么需不需要对每张纸都来一遍dp? 不用。因为我们发现转移式子是相同的，当(i,j)相同时，不同的纸的(dp[i][j])一定是相同的，所以我们只需要对那个被操作次数最多的纸进行dp就可以了。
(Code):

#include<iostream>
#include<cstdio>
#include<cstring>
#include<cmath>
#include<algorithm>
#include<queue>
using namespace std;
inline int read()
{
	char ch=getchar();
	int x=0;bool f=0;
	while(ch<'0'||ch>'9')
	{
		if(ch=='-')f=1;
		ch=getchar();
	}
	while(ch>='0'&&ch<='9')
	{
		x=(x<<1)+(x<<3)+(ch^48);
		ch=getchar();
	}
	return f?-x:x;
}
int n,c,k,mx,sum[109];
double ans,dp[109][109];
int main()
{
	freopen("paint.in","r",stdin);
	freopen("paint.out","w",stdout);
	n=read();c=read();k=read();
    while(k--)
    {
    	int l=read(),r=read();
    	for(int i=l;i<=r;i++)
    	 sum[i]++,mx=max(mx,sum[i]);
	}
	dp[0][1]=1;
	for(int i=1;i<=mx;i++)
		for(int j=0;j<c;j++)
		{
			for(int k=0;k<c;k++)
			 dp[i][j*k%c]+=1.0*dp[i-1][j]/(c*2);//1.0是为了保证答案是浮点数 
			dp[i][j]+=1.0*dp[i-1][j]/2; 
		}
	for(int i=1;i<=n;i++)
		for(int j=0;j<c;j++)
			ans+=dp[sum[i]][j]*j;	
    printf("%.3lf",ans);
}

因为嫌大括号占行但又不想大括号不换行所以诞生了似乎更毒瘤的码风