洛谷P3366 最小生成树板子题
这篇博客介绍两个算法:Prim算法和Kruskal算法,两个算法各有优劣
一般来说当图比较稀疏的时候,Kruskal算法比较快
而当图很密集,Prim算法就大显身手了
下面是这两种算法的介绍
Prim算法
百度百科定义:传送门
好吧,其实当我第一眼看到这个东西的时候感觉和Dijkstra好像,但是学了之后发现其实区别还是很明显(并且好记)的
Dijkstra是维护从到源点的最短长度,而Prim则是维护到最小生成树的最短长度(其实就是到最小生成树上所有点的最短长度)
那么Prim到底是什么呢?
Prim的思想是将任意节点作为根,再找出与之相邻的所有边(用一遍循环即可),再将新节点更新并以此节点作为根继续搜,维护一个数组:dis,作用为已用点到未用点的最短距离。
Prim算法之所以是正确的,主要基于一个判断:对于任意一个顶点v,连接到该顶点的所有边中的一条最短边(v, vj)必然属于最小生成树(即任意一个属于最小生成树的连通子图,从外部连接到该连通子图的所有边中的一条最短边必然属于最小生成树)
举个栗子:
STEP 1
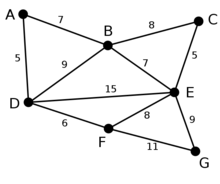
此为原始的加权连通图。每条边一侧的数字代表其权值。
STEP 2

顶点D被任意选为起始点。顶点A、B、E和F通过单条边与D相连。A是距离D最近的顶点,因此将A及对应边AD以高亮表示。
STEP 3
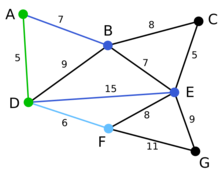
下一个顶点为距离D或A最近的顶点。B距D为9,距A为7,E为15,F为6。因此,F距D或A最近,因此将顶点F与相应边DF以高亮表示。
STEP 4

算法继续重复上面的步骤。距离A为7的顶点B被高亮表示。
STEP 5
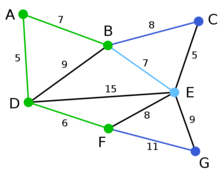
在当前情况下,可以在C、E与G间进行选择。C距B为8,E距B为7,G距F为11。点E最近,因此将顶点E与相应边BE高亮表示。
STEP 6
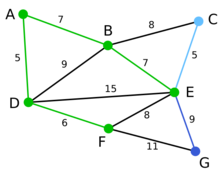
这里,可供选择的顶点只有C和G。C距E为5,G距E为9,故选取C,并与边EC一同高亮表示。
STEP 7

顶点G是唯一剩下的顶点,它距F为11,距E为9,E最近,故高亮表示G及相应边EG。
STEP 8
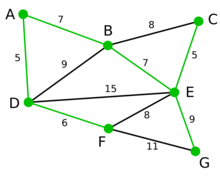
现在,所有顶点均已被选取,图中绿色部分即为连通图的最小生成树。在此例中,最小生成树的权值之和为39。
复杂度:
这里记顶点数v,边数e
邻接矩阵:O(v) 邻接表:O(elog2v)
下面是代码及注释:
#include<cstdio> #include<iostream> #include<cstdlib> #include<iomanip> #include<cmath> #include<cstring> #include<string> #include<algorithm> #include<time.h> #include<queue> using namespace std; typedef long long ll; typedef long double ld; typedef pair<int,int> pr; const double pi=acos(-1); #define rep(i,a,n) for(int i=a;i<=n;i++) #define per(i,n,a) for(int i=n;i>=a;i--) #define Rep(i,u) for(int i=head[u];i;i=Next[i]) #define clr(a) memset(a,0,sizeof a) #define pb push_back #define mp make_pair #define fi first #define sc second ld eps=1e-9; ll pp=1000000007; ll inf=2147483647; #define maxn 5005 #define maxm 200005 ll mo(ll a,ll pp){if(a>=0 && a<pp)return a;a%=pp;if(a<0)a+=pp;return a;} ll powmod(ll a,ll b,ll pp){ll ans=1;for(;b;b>>=1,a=mo(a*a,pp))if(b&1)ans=mo(ans*a,pp);return ans;} ll read(){ ll ans=0; char last=' ',ch=getchar(); while(ch<'0' || ch>'9')last=ch,ch=getchar(); while(ch>='0' && ch<='9')ans=ans*10+ch-'0',ch=getchar(); if(last=='-')ans=-ans; return ans; } //head struct edge { int to,_dis,next;////出边的终点、出边的长度、下一条出边 }edge[maxm<<1];//因为是无向图,所以开双倍数组,双倍快乐 int head[maxn],dis[maxn],cnt,n,m,tot,now=1,ans; //dis数组表示当前点到最小生成树的最短路径 bool vis[maxn]; inline void add_edge(int from,int to,int value) { edge[++cnt].to=to; edge[cnt]._dis=value; edge[cnt].next=head[from]; head[from]=cnt; }//添加边 inline int prim() { rep(i,2,n) dis[i]=inf;//初始化 for(int i=head[1];i;i=edge[i].next)//遍历当前节点的每一条出边 dis[edge[i].to]=min(dis[edge[i].to],edge[i]._dis);//重边の处理 while(++tot<n)//就是tot<=n-1,因为最小生成树的边数一定等于节点数-1 { int minn=inf;//初始化min vis[now]=1;//已经到达 rep(i,1,n) if(!vis[i]&&minn>dis[i])//寻找到最小生成树距离最短的节点 minn=dis[i],now=i;//更新 ans+=minn;//更新最小生成树 for(int i=head[now];i;i=edge[i].next)//遍历每一条出边 { int to=edge[i].to; if(dis[to]>edge[i]._dis&&!vis[to]) dis[to]=edge[i]._dis;//更新dis数组 } } return ans; } int main() { n=read(),m=read(); rep(i,1,m) { int from=read(),to=read(),value=read(); add_edge(from,to,value);//因为是无向图 add_edge(to,from,value);//双倍存储,双倍快乐 } cout<<prim(); }
Kruskal算法
Kruskal算法的思想比Prim好理解一些。先把边按照权值进行排序,用贪心的思想优先选取权值较小的边,并依次连接,若出现环则跳过此边(用并查集来判断是否存在环)继续搜,直到已经使用的边的数量比总点数少一即可。
证明:刚刚有提到:如果某个连通图属于最小生成树,那么所有从外部连接到该连通图的边中的一条最短的边必然属于最小生成树。所以不难发现,当最小生成树被拆分成彼此独立的若干个连通分量的时候,所有能够连接任意两个连通分量的边中的一条最短边必然属于最小生成树
上面提到:这个东西要用到“并查集”
不了解的:传送门
代码及注释:
#include<cstdio> #include<iostream> #include<cstdlib> #include<iomanip> #include<cmath> #include<cstring> #include<string> #include<algorithm> #include<time.h> #include<queue> using namespace std; typedef long long ll; typedef long double ld; typedef pair<int,int> pr; const double pi=acos(-1); #define rep(i,a,n) for(int i=a;i<=n;i++) #define per(i,n,a) for(int i=n;i>=a;i--) #define Rep(i,u) for(int i=head[u];i;i=Next[i]) #define clr(a) memset(a,0,sizeof a) #define pb push_back #define mp make_pair #define fi first #define sc second ld eps=1e-9; ll pp=1000000007; ll inf=2147483647; #define maxn 5005 #define maxm 200005 ll mo(ll a,ll pp){if(a>=0 && a<pp)return a;a%=pp;if(a<0)a+=pp;return a;} ll powmod(ll a,ll b,ll pp){ll ans=1;for(;b;b>>=1,a=mo(a*a,pp))if(b&1)ans=mo(ans*a,pp);return ans;} ll read(){ ll ans=0; char last=' ',ch=getchar(); while(ch<'0' || ch>'9')last=ch,ch=getchar(); while(ch>='0' && ch<='9')ans=ans*10+ch-'0',ch=getchar(); if(last=='-')ans=-ans; return ans; } //head struct Edge { int from,to,_dis; }edge[maxm]; int fa[maxn],n,m,ans,eu,ev,cnt; //father数组用来存储父亲节点 bool cmp(Edge a,Edge b) { return a._dis<b._dis;//比较函数 } inline int find_die(int x) { while(x!=fa[x]) x=fa[x]=fa[fa[x]]; return x;//找爹 } inline int kruskal() { sort(edge+1,edge+1+m,cmp);//先将所有的边按权值排序 rep(i,1,m) { eu=find_die(edge[i].from); ev=find_die(edge[i].to);//分别找始点和终点的祖宗节点 if(eu==ev)//如果是一个祖宗,就说明他们在一个联通图中 continue; ans+=edge[i]._dis;//更新最小生成树长度 fa[ev]=eu;//顺便标记父亲 if(++cnt==n-1)//知道生成最小生成树 break; } return ans; } int main() { n=read(),m=read(); rep(i,1,n) fa[i]=i;//初始化自己是自己的父亲 rep(i,1,m) edge[i].from=read(),edge[i].to=read(),edge[i]._dis=read(); cout<<kruskal(); }
加上判断无解的情况:
#include<cstdio> #include<iostream> #include<cstdlib> #include<iomanip> #include<cmath> #include<cstring> #include<string> #include<algorithm> #include<time.h> #include<queue> using namespace std; typedef long long ll; typedef long double ld; typedef pair<int,int> pr; const double pi=acos(-1); #define rep(i,a,n) for(int i=a;i<=n;i++) #define per(i,n,a) for(int i=n;i>=a;i--) #define Rep(i,u) for(int i=head[u];i;i=Next[i]) #define clr(a) memset(a,0,sizeof a) #define pb push_back #define mp make_pair #define fi first #define sc second ld eps=1e-9; ll pp=1000000007; ll inf=2147483647; #define maxn 500001 #define maxm 1000001 ll mo(ll a,ll pp){if(a>=0 && a<pp)return a;a%=pp;if(a<0)a+=pp;return a;} ll powmod(ll a,ll b,ll pp){ll ans=1;for(;b;b>>=1,a=mo(a*a,pp))if(b&1)ans=mo(ans*a,pp);return ans;} ll read(){ ll ans=0; char last=' ',ch=getchar(); while(ch<'0' || ch>'9')last=ch,ch=getchar(); while(ch>='0' && ch<='9')ans=ans*10+ch-'0',ch=getchar(); if(last=='-')ans=-ans; return ans; } //head struct Edge { int from,to,_dis; }edge[maxm]; int fa[maxn],n,m,ans,eu,ev,cnt; //father数组用来存储父亲节点 bool cmp(Edge a,Edge b) { return a._dis<b._dis;//比较函数 } inline int find_die(int x) { while(x!=fa[x]) x=fa[x]=fa[fa[x]]; return x;//找爹 } int main() { n=read(),m=read(); rep(i,1,n) fa[i]=i;//初始化自己是自己的父亲 rep(i,1,m) edge[i].from=read(),edge[i].to=read(),edge[i]._dis=read(); sort(edge+1,edge+1+m,cmp);//先将所有的边按权值排序 rep(i,1,m&&cnt<=n-1) { eu=find_die(edge[i].from); ev=find_die(edge[i].to);//分别找始点和终点的祖宗节点 if(eu==ev)//如果是一个祖宗,就说明他们在一个联通图中 continue; ans+=edge[i]._dis;//更新最小生成树长度 fa[ev]=eu;//顺便标记父亲 cnt++; } if(cnt!=n-1) cout<<"orz"; else cout<<ans; }
码字不易,如果看的满意请点个推荐哦~