我太菜了
T2
只需要找出从最大点走到最小点或者从最小点走到最大点就行了
考虑从每个点出发能走到的所有点当中最小的点是多少以及从这个点向回走的的最小值
枚举每一个点作为起点或者终点
答案只有两种情况:min->max max->min
直接枚举max是哪个点
对于每个点正着bfs并且反着bfs就好了
优化:对于每个点算他正着走和反着走的答案,每次都bfs是算法慢的原因。我们发现先算1号点再算2号点和倒过来是一样的
所以我们直接把点权从小到大排序,然后一个点一个点去处理所有的答案
如果最小的点能到这个点那这个点一定是从自己开始向前走最小的点。
直接标记一下这个点向前走最小的点是多少
也就是bfs的过程只需要bfs到没有算过答案的点就好了,同理这个点能到达的所有点都不用被算了。在这种方法下每个点只会被bfs一次
代码:
#include<cstdio> #include<cstdlib> #include<cstring> #include<algorithm> #include<queue> using namespace std; const int maxn=100010; const int maxm=500010; int n,m,en,result[maxn],z[maxn],y[maxn]; struct edge { int s,e; bool rev; edge *next; }*v[maxn],ed[maxm<<1]; void add_edge(int s,int e) { en++; ed[en].next=v[s];v[s]=ed+en;v[s]->e=e;v[s]->rev=false; en++; ed[en].next=v[e];v[e]=ed+en;v[e]->e=s;v[s]->rev=true; } //直接双向建边,因为bfs要两边跑。不过要注意标记哪一条真实存在 bool cmp(int a,int b) { return z[a]<z[b]; } void bfs(int p) { queue<int> q; if (!result[p]) result[p]=z[p];//表示已经有答案了 q.push(p); while (q.size()) { int now=q.front(); q.pop(); for (edge *e=v[now];e;e=e->next) if (!e->rev && !result[e->e])//遍历真实存在的边 { result[e->e]=z[p]; q.push(e->e); } } q.push(p); while (q.size()) { int now=q.front(); q.pop(); for (edge *e=v[now];e;e=e->next) if (e->rev && !result[e->e])//遍历反着的边 { result[e->e]=z[p]; q.push(e->e); } } } int main() { scanf("%d%d",&n,&m); for (int a=1;a<=n;a++) scanf("%d",&z[a]); for (int a=1;a<=m;a++) { int s,e; scanf("%d%d",&s,&e); add_edge(s,e); } for (int a=1;a<=n;a++) y[a]=a; sort(y+1,y+n+1,cmp); for (int a=1;a<=n;a++) bfs(y[a]); int ans=0; for (int a=1;a<=n;a++) ans=max(ans,z[a]-result[a]); printf("%d ",ans); return 0; }
T3
这是个很有思维难度的题。看数据范围很容易想到状压
f[s]表示s所对应的这些人之间能不能通过交换变的合法
把这些人排一个序,只需要检查能否两两组成一对就可以了
设排序之后数组为c[1],c[2],....c[2n-1],c[2n]
答案最大不超过人的个数-1,也就是n-1
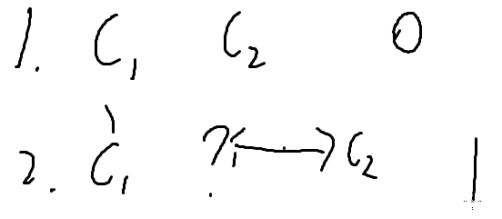
每次交换至少搞定一个人
设g[s]为我要让s这些人都合法所需要的最少交换次数
如果s的二进制位上有k个1,那么答案<=k-1
初始化g[s]=k-1,代表总有一种方法是k-1,现在需要找比k-1更小的数
怎么找?N<=16告诉我们,现在应该枚举子集了。
枚举s’,剩下的部分是s^s’
如果这两个部分都能自己解决的话,答案就缩小到了n-2
那么问题就变成了:最多能把n个人分成多少个部分,使得每一个部分都能自己解决
所以g[s]也就表示最多能把s分成多少个部分使得每个部分都能自己解决
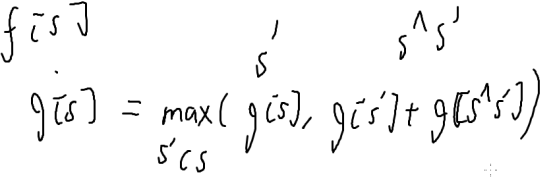
g[s]=max(g[s],g[s’]+g[s^s’]) (s’∈s)
Ans=n-g[2^n-1]