众所周知,tarjan是个非常nb的人,他发明了很多nb的算法,tarjan算法就是其中一个,它常用于求解强连通分量,割点和桥等。虽然具体实现的细节不太一样,但是大体思路是差不多的。先来说一下大体思路。
强连通分量,缩点
我们先来定义几个东西
时间戳:在搜索树中被遍历到的次序
比如在下图中
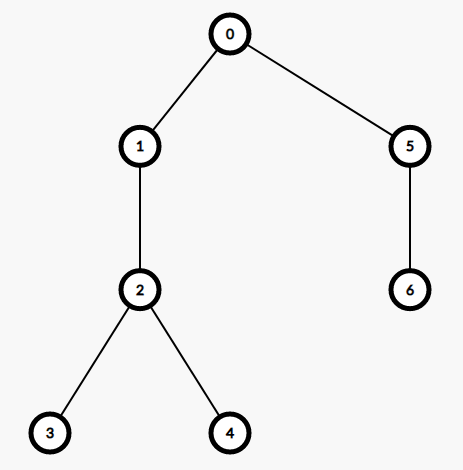
每个节点按照遍历顺序编的号就是它的时间戳
dfn[i]:表示第i个点的时间戳
low[i]:表示点i及i的子树所能追溯到的最早的节点的时间戳
low数组看起来很难理解是不是?
先来看一张非常经典的图

我们发现对于结点1,3,2,4,它们的low值都是1。为什么呢?因为这些点都直接或者间接的能够追溯到的最早的点1,而点1的dfn值为1,所以这些点的low值自然也就是1了
我们可以通过手算发现图中有三个强连通分量:{1,2,3,4},{5},{6}
我们发现,每一个连通分量都有一个点(以下称为代表点)的low值=dfn值,也就是说这个点及它的子树所能到达的最早的点就是他自己。
于是可以知道,对于dfn=low的点就是这一个强连通分量的代表点
那么要求强连通分量,实际上就是求有多少个点的low=dfn
用一个栈来实现,寻找low时只在栈里面找,弹出时不断从栈顶弹出直到弹出这个点
代码:
int dfn[50005],low[50005]; //dfn表示时间戳 //low表示点i及i的子树所能追溯到的最早的节点的时间戳 int ind; //ind表示遍历顺序 int in[50005],s[50005],top; //in表示当前这个点是否在队列中 //s是模拟的栈 //top是栈顶 int cnt_scc; //强连通分量的个数 int scc[50005],cntscc[50005]; //scc表示每一个点属于哪一个强连通分量 //cntscc表示强连通分量的大小 void tarjan(int x) { dfn[x]=++ind; low[x]=dfn[x];//初始化 s[top++]=x;//入栈 in[x]=1; for(int i=head[x];i;i=edg[i].nxt) { int v=edg[i].to; if(!dfn[v]) //如果是没有遍历到的树边就先对它进行操作 { tarjan(v); low[x]=min(low[x],low[v]);//更新low值 } else { if(in[v])//如果遍历过并且在栈中 //为什么一定要在栈中? //因为如果不在栈中说明它已经属于其他强连通分量了 //而每一次出栈都会弹出完整的强连通分量,所以这个点肯定不会产生影响 { low[x]=min(low[x],dfn[v]); } } } if(dfn[x]==low[x])//如果找到强连通分量的代表点 { cnt_scc++; while(s[top]!=x)//出栈 { top--; in[s[top]]=0; scc[s[top]]=cnt_scc; cntscc[cnt_scc]++; } } }
来看几道例题:
P2341 [HAOI2006]受欢迎的牛
如果有环,意味着这个环里的牛都互相喜欢
我们可以先求出环,然后把每一个环都看作一个点,这样整个图就变成了一个DAG(有向无环图)
看有几个点出度为0,如果大于一个点没有出边,就说明没有最受欢迎的牛,因为必定有一对牛相互不服
如果只有一个,那么强联通分量的大小就是答案
代码:
#include<bits/stdc++.h> using namespace std; int n,m; int cnt,head[50000]; struct edge { int to,nxt; }edg[50005]; inline void add(int from,int to) { edg[++cnt].to=to; edg[cnt].nxt=head[from]; head[from]=cnt; } int dfn[50005],low[50005],ind,in[50005]; int s[50005],top; int cnt_scc; int scc[50005],cntscc[50005]; void tarjan(int x) { dfn[x]=++ind; low[x]=dfn[x]; s[top++]=x; in[x]=1; for(int i=head[x];i;i=edg[i].nxt) { int v=edg[i].to; if(!dfn[v]) { tarjan(v); low[x]=min(low[x],low[v]); } else { if(in[v]) { low[x]=min(low[x],dfn[v]); } } } if(dfn[x]==low[x]) { cnt_scc++; while(s[top]!=x) { top--; in[s[top]]=0; scc[s[top]]=cnt_scc; cntscc[cnt_scc]++; } } } int out[50005]; int ans; int main() { scanf("%d%d",&n,&m); for(int i=1,x,y;i<=m;i++) { scanf("%d%d",&x,&y); add(x,y); } for(int i=1;i<=n;i++) { if(!dfn[i]) tarjan(i); } for(int i=1;i<=n;i++) { for(int j=head[i];j;j=edg[j].nxt) { int k=edg[j].to; if(scc[i]!=scc[k]) out[scc[i]]++; } } for(int i=1;i<=cnt_scc;i++) { if(!out[i]) { if(!ans) ans=i; else { cout<<0; return 0; } } } cout<<cntscc[ans]; }
我们发现如果这个题有环,那么不论在这个环上哪一个点开始传递信息,这个环中其他的点都可以到达,那么可以用tarjan把环缩成点。为了使每一个点都能被传递到,只需要找到所有入度为0的点,在这些点上开始传递信息就好了
代码:
#include<bits/stdc++.h> using namespace std; int n,m; int head[100005],cnt; struct edge { int to,nxt; }edg[500005]; inline void add(int from,int to) { edg[++cnt].to=to; edg[cnt].nxt=head[from]; head[from]=cnt; } int low[100005],dfn[100005],ind; int s[100005],top; bool in[100005]; int scc[100005],cnt_scc; inline void tarjan(int x) { dfn[x]=++ind; low[x]=dfn[x]; in[x]=1; s[top++]=x; for(int i=head[x];i;i=edg[i].nxt) { int v=edg[i].to; if(!dfn[v]) { tarjan(v); low[x]=min(low[x],low[v]); } else { if(in[v]) low[x]=min(low[x],dfn[v]); } } if(low[x]==dfn[x]) { cnt_scc++; while(s[top]!=x) { in[s[--top]]=0; scc[s[top]]=cnt_scc; } } } int ans; int gin[100005]; int main() { cin>>n>>m; for(int i=1;i<=m;i++) { int x,y; scanf("%d%d",&x,&y); if(x!=y) add(x,y); } for(int i=1;i<=n;i++) { if(!dfn[i]) tarjan(i); } for(int i=1;i<=n;i++) { for(int j=head[i];j;j=edg[j].nxt) { int v=edg[j].to; if(scc[v]!=scc[i]) { gin[scc[v]]++; } } } for(int i=1;i<=cnt_scc;i++) { if(!gin[i]) ans++; } cout<<ans; }
类似的题还有洛谷1262,这里就先不说了
tarjan求割点
什么是割点?
给你一张连通图,在上面找一个点,如果去掉这个点和所有连着它的边,整个图就不能保持连通,那么这个点就是割点
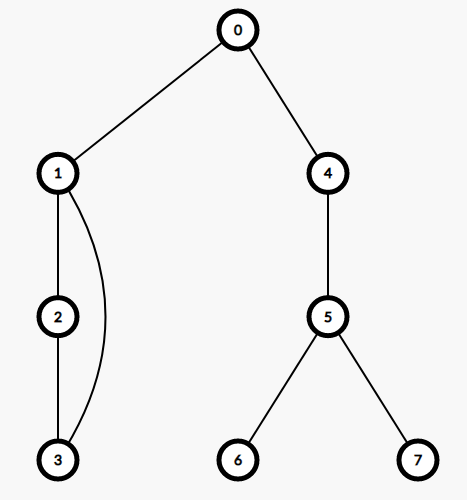
比如这张图,里面的割点有1,4,5
怎么求割点?
首先选定一个dfs树的树根,从这个点开始遍历整张图。
对于根节点,判断是不是割点显然只需要看他的子树的个数是不是大于等于2
对于非根节点x,如果存在儿子节点y,使得dfn[x]<=low[y],则x一定是割点。
显然如果x的所有儿子能够不经过x直接到达他的祖先,这个点就一定不是割点;反之,则说明去掉它一定会改变图的连通性
代码:
int low[20005],dfn[20005],ind,ans; bool cut[20005]; inline void tarjan(int x,int fa) { dfn[x]=++ind; low[x]=dfn[x]; int ch=0; for(int i=head[x];i;i=edg[i].nxt) { int v=edg[i].to; if(!dfn[v]) { tarjan(v,fa); low[x]=min(low[x],low[v]); if(low[v]>=dfn[x]&&x!=fa) cut[x]=1; if(x==fa) ch++; } else { low[x]=min(low[x],dfn[v]); } } if(x==fa&&ch>=2) cut[fa]=1; }
例:
P3388 【模板】割点(割顶)
#include<bits/stdc++.h> using namespace std; int n,m; int head[20005],cnt; struct edge { int to,nxt; }edg[200005]; inline void add(int from,int to) { edg[++cnt].to=to; edg[cnt].nxt=head[from]; head[from]=cnt; } int low[20005],dfn[20005],ind,ans; bool cut[20005]; inline void tarjan(int x,int fa) { dfn[x]=++ind; low[x]=dfn[x]; int ch=0; for(int i=head[x];i;i=edg[i].nxt) { int v=edg[i].to; if(!dfn[v]) { tarjan(v,fa); low[x]=min(low[x],low[v]); if(low[v]>=dfn[x]&&x!=fa) cut[x]=1; if(x==fa) ch++; } else { low[x]=min(low[x],dfn[v]); } } if(x==fa&&ch>=2) cut[fa]=1; } int main() { cin>>n>>m; for(int i=1;i<=m;i++) { int x,y; scanf("%d%d",&x,&y); add(x,y); add(y,x); } for(int i=1;i<=n;i++) { if(!dfn[i]) tarjan(i,i); } for(int i=1;i<=n;i++) { if(cut[i]==1) ans++; } cout<<ans<<endl; for(int i=1;i<=n;i++) { if(cut[i]) printf("%d ",i); } }