序列上的dp状态设计最基本的形式
F[i]表示以i结尾的最优值或方案数。
F[i][k]表示以i结尾附加信息为k的最优值或方案数。
当然可以有多维附加信息。
转移的话往往是枚举上一个断点。
F[i]=max { F[j]+ w(j+1,i) | j是一个满足转移条件的断点}。
另一个很常见的是:f[i][j]前i个位置分成j段/选出j个的最优值。
这是最简单的一类序列上的dp。
bzoj1003
有m个码头和e条航线,每天航线有成本。有连续n天需要从1号码头到m 号码头运输货物。每个码头会在某些天数区间内不许经过。每更换一次运输路线,要付出k的成本。
求这n天的最小总成本。
m<=20,n<=100
其实就是分成很多段,每一段选同一个运输路线,然后得到一个最优的划分方案使得成本最小。
f[i]表示前i天的运输最小成本。
f[i]=min{ f[j]+k+w(j+1,i)*(i-j) | j<i}
其中w(x,y)表示最短的在第x天到第y天都能用的路线长度,把能在这几天一直走的点加进图中,跑最短路径即可。
复杂度O(N^2 * m * log(m))
bzoj1296 粉刷匠
有n条木板要被粉刷,每条木板分为m个格子,每个格子需要被刷成蓝色或红色。
每次粉刷可以在一条木板上给连续的一段格子刷上相同的颜色。每个格子最多被刷一次。
问若只能刷k次,最多正确粉刷多少格子。
n,m<=50,k<=2500
如果只有一条木板,那么设g[i][j]表示前i个格子刷j次的最多正确格子
g[i][j]=max{ g[k][j-1]+w(k+1,i) | k<i}
w(x,y)为第x到第y个格子的最多同色格子数,哪个颜色出现的多刷哪个,直接记一个前缀和即可。
有多条木板,设f[i][j]表示前i个木板刷j次的最大答案。
f[i][j]=Max{ f[i-1][k]+gi [m][j-k] | k<=j }
复杂度:O(n* m^3) O(n*k*n)
其实像这种一般的dp,就是把影响答案的信息用多维状态来表示,什么必要什么就放在状态里。
括号序列模型及解法
Codeforces314E
给定一个长度为n的仅包含左右括号和问号的字符串,将问号变成左括号 或右括号使得该括号序列合法,求方案总数。
例如(())与()()都是合法的括号序列。
n<=3000。
括号序列问题,往往就是把左括号看成+1,右括号看成-1,我们只需要保证任意一个前缀大于等于0,且总和为0,就代表是个合法括号序列了。
令dp[i][j]表示当前到第i个字符,前缀和为j的方案数。(j>=0)
那么分三种情况考虑。
若第i+1个字符是+1,则能转移到dp[i+1][j+1]。
若第i+1个字符是-1,则能转移到dp[i+1][j-1]。
若第i+1个字符是问号,则能转移到dp[i+1][j-1]与dp[i+1][j+1]。
最终dp[n][0]就是方案总数啦。
bzoj4922
给出一些括号序列,要求选择一些括号序列拼接成一个合法的括号序列,使得总长最大。
1<=n<=300,表示括号序列的个数
括号序列的长度len不超过300.
对于任意一个括号序列都可以化简成数对(x,y)表示去掉完整的括号后有x个)y个(
然后考虑假如我们的子集选好了,我们要按照什么顺序拼接才能拼成一个合法的括号序列呢?
这就转化成了另一个问题:BZOJ3709。
BZOJ3709
在一款电脑游戏中,你需要打败n只怪物(从1到n编号)。为了打败第i只怪物,你需要消耗d[i]点生命值,但怪物死后会掉落血药,使你恢复a[i]点生命值。任何时候你的生命值都不能降到0(或0以下)。
请问是否存在一种打怪顺序,使得你可以打完这n只怪物而不死掉。
N<=10^5
贪心:noip的贪心很多都是按照某种方式排序,然后依次选或处理。
我们来看看应该怎么排序。
关于本题:
1:如果a[i]-d[i]>0,说明打掉这个怪兽有血可恢复,那么血量会变多,明显我们按照伤害d[i]从小到大排序即可,然后一个个杀下来。因为这样才能保证尽可能不死。
2:如果a[i]-d[i]<0,说明会亏血。一个精妙的想法就是,最后剩余的血量值,假设是x,那么x是固定的。然后可以看作初始血量为x,怪兽的属性a,d交换,这样就和上一种情况一样了。因为是反着看的,所以最后在倒过来,按照血药的回血量从大到小排序就好了(如图)

回到这个题
我们还是把左括号看成+1,右括号看成-1,同样是保证任意一个前缀大于等于0,且总和为0。
那就是每一个给定的序列都是 先-Li再+Ri,Ri是对消后左端右括号的数量,Li是对消后右端左括号的数量。然后依次拼起来之后任何一个前缀都大于等于0
我们按照上一题的做法排序即可,排序后我们从左往右做dp。
dp[i][j]表示考虑了前i个括号序列,当前的前缀和为j
设f[i][j]为前i个的前缀和为j时选出括号序列最长的长度和。
也就是前i个括号序列左括号比右括号多j个时的最长的长度和。
转移时考虑下一个括号序列选不选即可。
Len[i]为排完序后第i个括号序列的长度。
f[i+1][j-L[i+1]+R[i+1]]<--f[i][j] + len[i+1] (j>=L[i+1])
f[i+1][j]<--f[i][j]
最后答案就是f[n][0]. 复杂度O(n*len*len)
一套有趣的题目
1:1,2,3…n 依次进栈,求有多少种可能的出栈序列。
2:由n对括号形成的合法的括号序列有多少个。
3:n个节点共能构成多少种二叉树,左右子树是认为不同。
4:凸多边形的三角划分的方案数:把一个凸多边形用n-3条直线连接n-3对 顶点,共形成n-2个三角形,求方案数。
5:一个n*n的格子,从(0,0)走到(n,n),求不跨过(0,0)->(n,n)这条直线的路径方案数。
N<=10^5
f[n]表示n对括号的方案数
f[n]=Σf[i]*f[n-1-i](i=0~n-1)
卡特兰数
我们设f[n]表示n个数依次进栈所能形成的出栈序列数。
似乎和之前不一样,好像不是划分成一段一段那样的简单形式。
我们可以考虑另一种形式的状态转移方式,以转移到子问题。
注意一段一段划分我们可以枚举最后一段的起点,但是这里不是一段一段的,我们要考虑另外的转移方式。
实际上我们发现我们可以枚举1这个数是什么时候出栈的。
那么我们可以得到
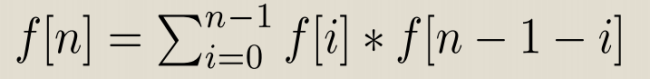
注意n的卡特兰数是n+2边形的方案数
有n个数,选择其中若干数,使得每连续k个数中都至少有一个数被选中,且选出的数的和最小。
k<=n<=1000。
k<=n<=100000。
dp[i]=min{dp[j]|j>=i-k}+a[i]
滑动窗口问题,单调队列优化

Vocabulary简化版
给定3个等长的只包含“?”或小写字母的字符串s,其中“?”表示可能是任意一个小写字母。
已知3个字符串的字典序是升序的且互不相同。
问方案总数。
|s|<=1000。
|s|<=100000。
|s|<=1000。
设dp[i][0/1][0/1]表示前i个前缀,第一串和第二串是否相等,第二串和第三串是否相等的方案数
枚举每一个?填什么即可
|s|<=100000。
辅助数组优化
f[i][j][k][0/1][0/1][0/1][0/1]
表示下一个位置,第一个串字符是i,第二个串字符是j,第三个串字符是k,由于可能出现”?”的情况,我们用0 表示”?”。前两个[0/1]表示之前的位置1和2串是否相等,2和3串是否相等,后两个[0/1]表示将下一个位置所有”?”用字母代替后,第1个串的与第二个串的是否相等,2和3串是否相等,在转移时直接拿f数组转移。
利用这个转移系数的数组做dp的时间复杂度就是O(n)的了。
预处理:枚举前五维,枚举问号是什么
区间dp状态设计的一般形式
区间dp一般就是设dp[i][j]表示区间[i,j]所能形成的最优答案或者方案数。
或者像序列一样,多加几维表示附加的信息。
poj3280
给你长度为m的字符串,其中有n种字符,每种字符都有两个值,分别是插入这个字符的代价,删除这个字符的代价,让你求将原先给出的那串字符变成一个回文串的最小代价。
M<=2000
dp[i][j]代表区间i到区间j成为回文串的最小代价,那么对于dp[i][j]有三种情况:
1、dp[i+1][j]表示区间i到区间j已经是回文串了的最小代价,那么对于s[i] 这个字母,我们有两种操作,删除与添加,对应有两种代价, dp[i+1][j]+add[s[i]]或dp[i+1][j]+del[s[i]],取这两种代价的最小值。
2、dp[i][j-1]表示区间i到区间j-1已经是回文串了的最小代价,那么对于s[j] 这个字母,同样有两种操作,dp[i][j-1]+add[s[j]]或dp[i][j-1]+del[s[j]],取最小值。
3、若是s[i]==s[j],dp[i+1][j-1]表示区间i+1到区间j-1已经是回文串的最小代价,那么对于这种情况,我们考虑dp[i][j]与dp[i+1][j-1]的大小
然后dp[i][j]取上面这些情况的最小值即可。
括号最大匹配
给你一串()[]括号,要你求出这串括号的最大匹配个数,如'('与')'匹配,为 2个,'['与']'匹配,为2个,其他不能匹配.......
允许有杂质即( [ ( [ ] ] ) ] 应该是 [ ( [ ] ) ]//去掉杂质
就是选出一个最长合法子括号序列。
序列的长度小于等于100。
dp[i][j]代表从区间i到区间j所匹配的括号的最大个数,首先,假设不匹配, 那么dp[i][j]=dp[i+1][j];
然后查找i+1~~j有木有与第i个括号匹配的,
有的话,dp[i][j]=max(dp[i][j],dp[i+1][k-1]+dp[k+1][j]+2)//其中c[i]与c[k]匹配。
为什么和上一题不一样?
因为()()()()….而非仅仅是(((())))
bzoj1900
折叠的定义如下:
1. 一个字符串可以看成它自身的折叠。
2. X(S)是X(X>1)个S连接在一起的串的折叠。记作X(S) = SSSS…S(X个S)。
3. 如果A = A’, B=B’,则AB =A’B’ 例如,因为3(A) = AAA, 2(B) = BB,所以
3(A)C2(B) = AAACBB,而2(3(A)C)2(B)=AAACAAACBB
给一个字符串,求它的最短折叠。例如AAAAAAAAAABABABCCD的最短折叠为:9(A)3(AB)CCD。
输入字符串长度小于等于100。
f[l][r]表示,把l~r这个区间折叠的最短长度,然后我们想,对于一个区间来说,我们有两种选择,一种是把这个区间它自己来折叠,另一种是两块已经折叠的区间接起来。
对于第二种情况,直接枚举断点(区间dp中很常见),找最小的一种方案,第一种则是,找出它所有的折叠方案,在折叠方案中取一个最优的。
思路的整理类比和分析:整体的思路都是对于一段区间,两类决策
1:枚举断点,由子问题更新的最优决策。
2:该区间本身进行压缩(进行处理)的最优决策。
一般1000考虑边界,100枚举断点
环形问题
环形问题有一个很常见的处理办法是,断环为链,然后把这个链复制一遍接在原链的后面。
然后做区间dp,最后取答案就是找dp[i][i+n-1]里面取最优的即可。
能量项链
在项链上有N颗能量珠。能量珠是一颗有头标记与尾标记的珠子,这些标记对应着某个正整数。并且,对于相邻的两颗珠子,前一颗珠子的尾标记一定等于后一颗珠子的头标记。如果前一颗能量珠的头标记为m,尾标记为r,后一颗能量珠的头标记为r,尾标记为n,则聚合后释放的能量为 m×r×n(Mars单位),新产生的珠子的头标记为m,尾标记为n。
需要时,Mars人就用吸盘夹住相邻的两颗珠子,通过聚合得到能量,直到项链上只剩下一颗珠子为止。显然,不同的聚合顺序得到的总能量是不同的,请你设计一个聚合顺序,使一串项链释放出的总能量最大。
◦N<=100
在读入的时候现将珠子们复制一遍放到后面,断环成链
◦设f[j][i]表示左端点为j号珠子,右端点为i号珠子的区间所能得到的最大能量,转移就枚举最后一步聚合的位置即可。
给定n堆石子a[i],排列成一个环,每次可以消去一堆石子,代价是这堆石子两边石子数的最大公约数,直到最后只剩两堆时,代价为这两堆石子数的最大公约数,这两堆石子直接消除。请问消去所有石子的最小代价是多少。
◦ n<=100
首先也是断环成链,同时倍长一下。
◦然后设dp[i][j]表示区间[i+1,j-1]全部消掉的最小代价是多少,剩下a[i]和a[j], 枚举最后一次消掉的数转移即可。
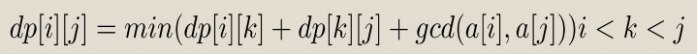
◦ dp[i][i+1]=0.
◦最后只需要枚举剩下的两个珠子x、y即可,取dp[x][y]+dp[y][x+n]的最大值 即可。