DAY 5
廖俊豪神仙出题
T1
最小差异矩阵(a.cpp, a.in, a.out)
【题目描述】
有一个 n*m 的矩阵,矩阵的每个位置上可以放置一个数。对于第 i 行,第 i 行的差异定义为该行的最大数和最小数的差。一个矩阵的差异,定义为矩阵中每一行差异的最大值。现在给定 k 个数 v[1..k],问:从这 k 个数中选 n*m 个数放入矩阵,能够得到的矩阵的差异最小值是多少。
【输入格式】
第一行三个整数,k, n, m,表示有 k 个数可选,矩阵的行数和列数分别为 n 和 m。
第二行 k 个整数,表示备选的数 v[1..k]。
【输出格式】
输出一个数,表示能够得到的最小差异值
【样例输入】
5 2 2
7 5 8 2 3
【样例输出】
1
【数据范围与提示】
对于 30%的数据,k <= 10, n <= 3, m <= 3
对于 100%的数据,n * m <= k <= 100000, n, m <= 1000,0 <= v[i] <= 10^9
256MB,1s
题解
先排序
二分差异的最大值k,然后贪心
放数一定是连续的,将某一段放到一行
从前往后找,如果说从某个数开始往后数m个数,最大值减去最小值小于等于枚举的k就合法,那么就把这m个数放到同一行,最后判断是否能够凑出n行
O(klogC)
#include<bits/stdc++.h> using namespace std; const int maxn = 1e5 + 7; int n, m, k, v[maxn]; int judge(int d) { int tmp = 0; for (int i=1; i+m-1<=k; ++i) { if (v[i+m-1] - v[i] <=d) ++tmp, i += m - 1; } if (tmp >= n) return 1; return 0; } int main() { freopen("a.in", "r", stdin); freopen("a.out", "w", stdout); scanf("%d%d%d", &k, &n, &m); for (int i=1; i<=k; ++i) scanf("%d", &v[i]); sort(v + 1, v + k + 1); int left = 0, right = 1e9; while (left < right) { int mid = (left + right) / 2; if (judge(mid)) right = mid; else left = mid + 1; } printf("%d ", left); return 0; }
T2
分割序列(b.cpp, b.in, b.out)
【题目描述】
给定一个长度为 n 的序列 v[1..n],现在要将这个序列分成 k 段(每段都不能为空),定义每一段的权值为该段上的所有数的或和。定义整个序列的权值为每段权值的和。问:这个序列的最大权值为多少。
【输入格式】
第一行两个数 n 和 k,意义如题意所示。
第二行 n 个数,表示这个序列 v[1..n]。
【输出格式】
输出一个数,代表这个序列的最大权值。
【输入样例】
5 2
7 5 8 2 3
【输出样例】
22
【数据范围与时空限制】
对于 30%的数据,n <= 10, k <= 10
对于 60%的数据,n <= 100, k <= 100
对于 100%的数据,k <= n <= 2000,1 <= v[i] <= 5 * 10^5
256MB,1s
题解
f[i][j]表示前i个数分j段的最大权值和 ans=f[n][k]
可以先预处理出每一段的或和sum[i][j]
转移:f[i][j]=max(f[l][j-1]+sum[l+1][i])(l<i) l表示将第i+1到第i个数当成一段

60pts
怎么优化?
还是先n^2预处理
找单调性 f[l][j-1]随着l的增加递增 sum[l+1][i]随着l的增加而递减
Sum是按位或:比如变化到1e6,最多变化20次

如果按sum值分段,那么最优的一定是某一段sum的最后加上f的值
那么对于每一个j,我们可以枚举它前面的点i,把sum分段
If(sum[i][j]!=sum[i+1][j]) vector[j].push_back(i);
在刚才枚举l的时候就可以变成枚举决策点了,这一维变成了log的复杂度

O(n*k*logC)
#include <bits/stdc++.h> using namespace std; const long long inf = 1ull << 30 << 20; const int maxn = 2005; vector<int> point[maxn]; int n, K, v[maxn], sum[maxn][maxn]; long long f[maxn][maxn]; int main() { freopen("b.in", "r", stdin); freopen("b.out", "w", stdout); cin >> n >> K; for (int i=1; i<=n; ++i) cin >> v[i]; for (int i=1; i<=n; ++i) sum[i][i] = v[i]; for (int i=1; i<n; ++i) for (int j=i+1; j<=n; ++j) sum[i][j] = sum[i][j-1] | v[j]; for (int i=1; i<=n; ++i) { point[i].push_back(i); for (int j=i-1; j>=1; --j) if (sum[j][i] != sum[j+1][i]) point[i].push_back(j); } for (int k=1; k<=K; ++k) for (int i=1; i<=n; ++i) { if (i < k) continue; for (int j=0; j<point[i].size(); ++j) { int x = point[i][j]; if (x >= k) f[i][k] = max(f[i][k], f[x-1][k-1] + sum[x][i]); } } cout << f[n][K] << endl; return 0; }
T3
树的魔法值(C.cpp, C.in, C.out)
【题目描述】
有一棵 k+1 层的满二叉树,那么该树有 2^k 个叶子节点。给定 n 个机器人(n=2^k),编号从 1—n,编号为 i 的机器人的权值为 v[i]。我们现在要将这 n 个机器人分别放置在这 n 个叶子节点上,每个叶子节点放且只能放一个机器人。叶子节点的权值为该叶子节点上的机器人的权值。非叶子节点的权值定义为该树中编号最大的机器人的权值。每个非叶子节点除了权值以外,还有一个魔法值,该点的魔法值为其左右儿子节点的权值的乘积。整棵树的魔法值定义为非叶子节点的魔法值的和。
问:将这 n 个机器人随机地放在这 n 个叶子节点上,树的魔法值的期望为多少。
【输入格式】
第一行为一个整数 k,含义如题所示。
第二行为 2^k 个整数,依次表示这 n 个机器人的权值。
【输出格式】
假设答案为一个不可约分数 P/Q,则输出在模 1e9+7 意义下的 P * (Q^-1)模 1e9+7 的值。
【样例输入 1】
2
1 3 5 7
【样例输出 1】
59
【样例解释】
对于 n=4 的情况,机器人共有 24 种不同的安放方案。其中,本质不同的有 3 种,分别是((1,3),(5,7)), ((1,5),(3,7)), ((1,7),(5,3)),魔法值分别为 1*3+5*7+3*7=59, 1*5+3*7+5*7=61,1*7+5*3+5*7=57, 答案为(57+59+61)/3 = 59。
【样例输入 2】
2
1 5 3 7
【样例输出 2】
333333390
【数据范围与时空限制】
30%的数据,k <= 3
60%的数据,k <= 10
100%的数据,k <= 18
256MB,1s
题解:
30pts k<=3 --> n<=8 n!暴力 期望:所有情况的值加起来取平均 就是除以n!
60pts k<=10,n<=1024 求出所有情况的魔法值的和?
考虑两个点x和y在第d层对答案的贡献
分步考虑 考虑两个点在第d层相遇,那么应该算清楚第d层相遇了多少次,统计出来就可以算出贡献
Σ(v[x]*v[y]*times[x][y])
怎么算?
设x>y
在y的子树里面,一定有2^d-1个小于y的

1)在y-1个数里面,选择2^d -1个小于y的方案数C(y -1, 2^y -1)
2)在x- 2^d -1个数里面,选择2^d -1个小于x的方案数 C(x- 2^d -1 , 2^d-1)
3) 其他n- 2^(d+1) 任意排列n- 2^(d+1)!
4) 考虑x和y相遇的位置 2^(k-d)
5) 上面的都不对,因为要求排列,所以是A
6) x和y的位置可以互换 *2
x>2^(d+1) y>=2^d x>y
bits[i]表示2^i
c[i][j]表示C(i,j)
fac[i]表示i!
枚举x,y,d
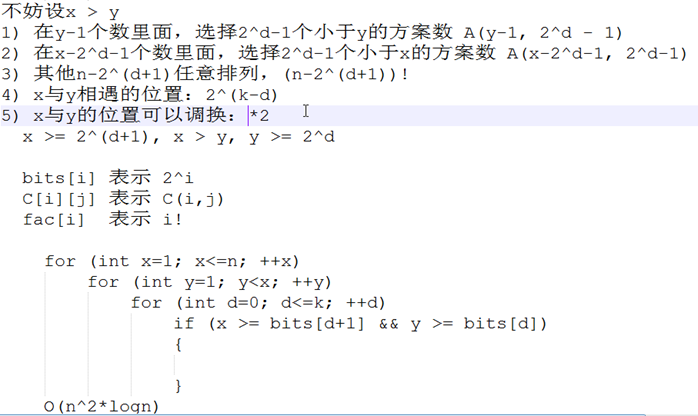
O(n^2logn)
100pts
优化式子本身
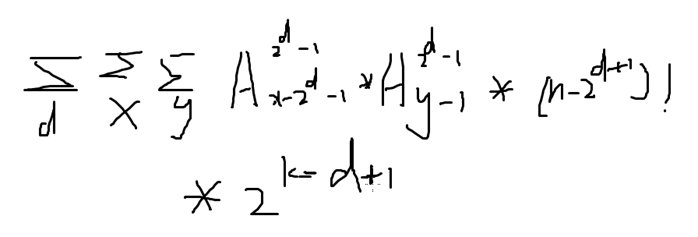
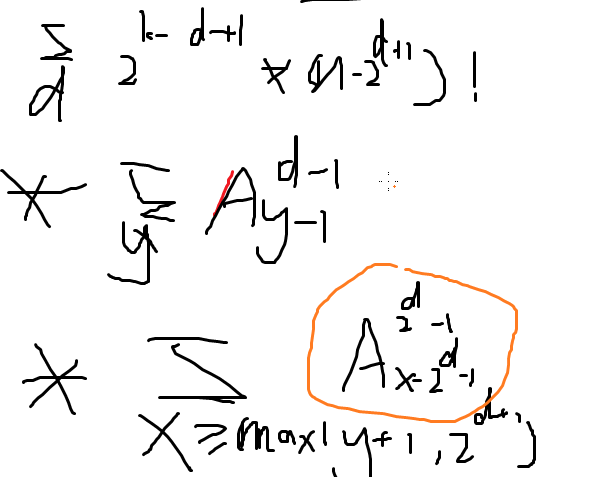
发现最后一部分只在枚举x的时候和y有关,所以可以把它放到外面去
预处理出后缀和,枚举d和y就行了
#include <bits/stdc++.h> using namespace std; const int mod = 1e9 + 7; const int maxn = (1 << 18) + 7; typedef long long LL; LL fac[maxn], inv_fac[maxn], bit[maxn], sum[maxn]; int n, v[maxn], k; int powmod(int x, int times) { LL tmp = 1; while (times > 0) { if (times & 1) tmp = tmp * x % mod; x = (LL)x * x % mod; times >>= 1; } return tmp; } LL C(int x, int y) { if (x < y) return 0; return fac[x] * inv_fac[y] % mod * inv_fac[x-y] % mod; } int main() { freopen("c.in", "r", stdin); freopen("c.out", "w", stdout); fac[0] = 1; for (int i=1; i<maxn; ++i) fac[i] = fac[i-1] * i % mod; inv_fac[maxn-1] = powmod(fac[maxn-1], mod - 2); for (int i=maxn-2; i>=0; --i) inv_fac[i] = inv_fac[i+1] * (i + 1) % mod; bit[0] = 1; for (int i=1; i<=20; ++i) bit[i] = bit[i-1] * 2; scanf("%d", &k); n = bit[k]; for (int i=1; i<=bit[k]; ++i) scanf("%d", &v[i]); //for (int i=bit[k]; i>=1; --i) scanf("%d", &v[i]); LL ans = 0; for (int d=1; d<=k; ++d) { LL tmp = 0; for (int i=n; i>=bit[d]; --i) sum[i] = (sum[i+1] + C(i-1-bit[d-1], bit[d-1]-1) * v[i]) % mod; for (int j=n-1; j>=bit[d-1]; --j) tmp = (tmp + C(j-1, bit[d-1]-1) * v[j] % mod * sum[max(bit[d], (LL)j + 1)]) % mod; ans = (ans + tmp * fac[bit[d-1]] % mod * fac[bit[d-1]] % mod * fac[n-bit[d]] % mod * 2 % mod * bit[k-d]) % mod; } ans = ans * inv_fac[n] % mod; cout << ans << endl; return 0; }