差分+线段树
首先看到题目中的区间修改,显然可以用线段树+差分做,于是就设每次区间修改的左端点为(1),右端点为(-1)。
考虑怎么利用已有的差分数组。
首先题目有一个值得说明的地方就是他一次操作埋下的地雷并不会覆盖之前埋下的地雷(我就因为这个浪费了一次提交)。
首先先看一组数据:
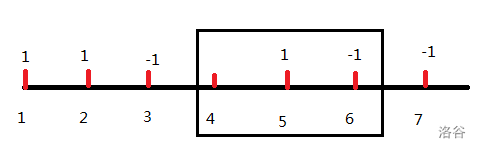
区间分别为([1,3],[2,7],[5,6]),查询区间([4,6]),经过手推得到答案应该是(2)。
让我们看看(2)怎么表示
区间([1,3])是在左端点之前结束的,所以它不会对答案造成影响。
区间([2,7])是覆盖了整个询问区间,显然会使答案+1。
区间([5,6])在询问区间内开始,在询问区间内结束,也对答案产生了影响。
稍微一思考,首先可以得到一个结论,区间并不重要,重要的是端点,因为我们只关心数量而不是具体的数。
那么显然在询问区间右端点以前的开始标记(包括右端点)会使答案(+1),在询问区间左端点以前的结束标记(不包括左端点)会使答案(-1)。
到了这里,我们就可以实现了。维护两棵线段树,一棵表示开始标记,记作(Tree1),另一棵表示结束标记,记作(Tree2)。那么每次查询的时候,记查询区间为([l,r])答案就是(Tree1[r]-Tree2[l-1])。
ac code:
#include<bits/stdc++.h>
using namespace std;
const int N = 100005;
int n, m;
struct Tree
{
int ad, ct;//add cut
}tree[N << 2];
void add1(int cnt, int l, int r, int x)
{
if(l == r)
{
tree[cnt].ad += 1;
return;
}
int mid = l + r >> 1;
if(mid >= x) add1(cnt << 1, l, mid, x);
if(mid < x) add1(cnt << 1 | 1, mid + 1, r, x);
tree[cnt].ad = tree[cnt << 1].ad + tree[cnt << 1 | 1].ad;
}
void add2(int cnt, int l, int r, int x)
{
if(l == r)
{
tree[cnt].ct += 1;
return;
}
int mid = l + r >> 1;
if(mid >= x) add2(cnt << 1, l, mid, x);
if(mid < x) add2(cnt << 1 | 1, mid + 1, r, x);
tree[cnt].ct = tree[cnt << 1].ct + tree[cnt << 1 | 1].ct;
}
int query1(int cnt, int l, int r, int nl, int nr)
{
if(l >= nl && r <= nr) return tree[cnt].ad;
int mid = l + r >> 1, ans = 0;
if(mid >= nl) ans += query1(cnt << 1, l, mid, nl, nr);
if(mid < nr) ans += query1(cnt << 1 | 1, mid + 1, r, nl, nr);
return ans;
}
int query2(int cnt, int l, int r, int nl, int nr)
{
if(l >= nl && r <= nr) return tree[cnt].ct;
int mid = l + r >> 1, ans = 0;
if(mid >= nl) ans += query2(cnt << 1, l, mid, nl, nr);
if(mid < nr) ans += query2(cnt << 1 | 1, mid + 1, r, nl, nr);
return ans;
}
int main()
{
scanf("%d%d", &n, &m);
for(int i = 1, q, l, r; i <= m; i ++)
{
scanf("%d%d%d", &q, &l, &r);
if(q == 1) add1(1, 1, n, l), add2(1, 1, n, r);
else if(q == 2)
{
printf("%d
", query1(1, 1, n, 1, r) - query2(1, 1, n, 1, l - 1));
}
}
}