机器学习——05线性回归算法

1.本节重点知识点用自己的话总结出来，可以配上图片，以及说明该知识点的重要性

线性回归就是对大量的观测数据进行处理，从而得到比较符合事物内部规律的数学表达式。也就是说寻找到数据与数据之间的规律所在，从而就可以模拟出结果，也就是对结果进行预测。解决的就是通过已知的数据得到未知的结果。简而言之就是通过大量数据的分析来寻找规律，如果是线性关系就利用线性回归算法模型来预测某一数据。真实值与预测值之间的误差为损失值，可以用梯度下降法减少损失。

 ①机器学习的分类

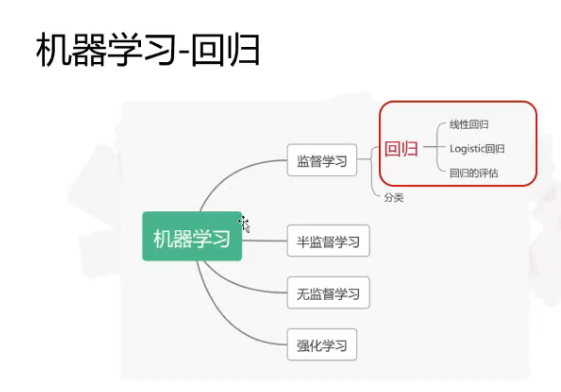
 ②回归算法的含义

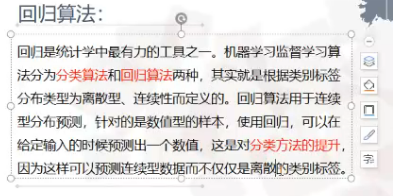
 ③回归和分类的区别

 ④线性回归的含义

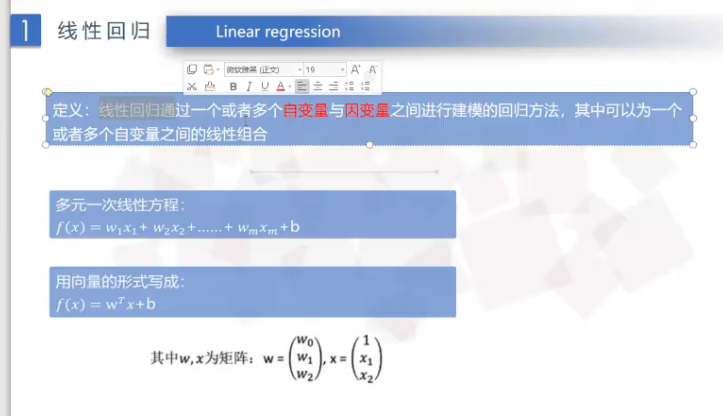
 ⑤矩阵：矩阵必须是二维的

 ⑥损失函数（重点）：损失函数值越小，说明误差也小，模型预测结果越准确。

 ⑦梯度下降法：这个方法可以减少损失值，让模型更加准确。

2.思考线性回归算法可以用来做什么？（大家尽量不要写重复）

可以收集之前几个季度电影关注度、票房以及价格的数据，将其分为不同类型的电影题材，利用线性回归算法在其类里面根据关注度来预测即将播出的电影的票房或者价格。还可以根据不同数据预测天气，空气质量，房价，销售额等。

3.自主编写线性回归算法 ，数据可以自己造，或者从网上获取。（加分题）

①数据：上学期爬取的东方财富网数据

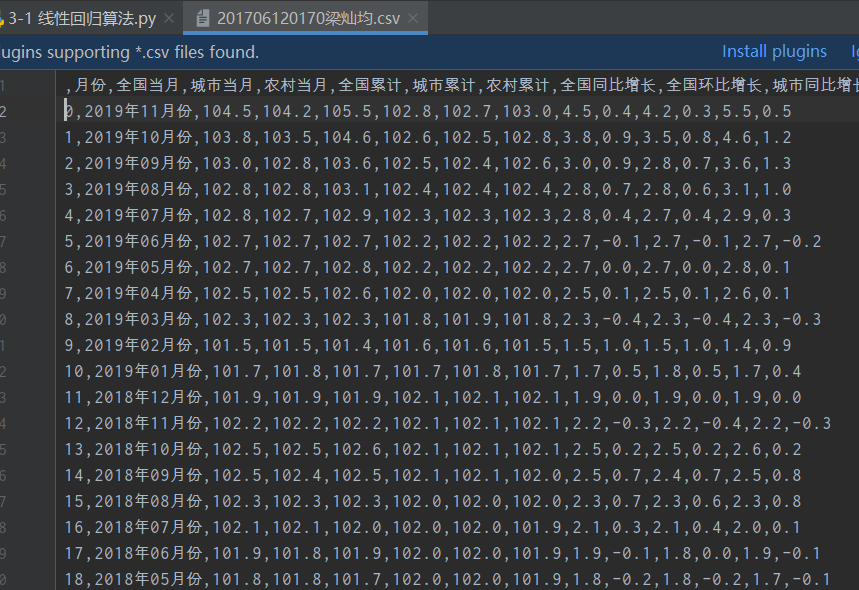
②代码：

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
data = pd.read_csv('./data/201706120170梁灿均.csv')
X=data.iloc[:,8]
Y=data.iloc[:,10]
np.array(X)
np.array(Y)
X=X.values.reshape(-1,1)#扁平化，就是features只能为1
Y=Y.values.reshape(-1,1)
from sklearn.linear_model import LinearRegression
from sklearn.preprocessing import PolynomialFeatures
from sklearn.pipeline import Pipeline

def polynomial_model(degree=1):
    polynomial_features=PolynomialFeatures(degree=degree,include_bias=False)#生成degree阶多项式
    linear_regression=LinearRegression(normalize=True)#线性回归实例化，并且正规化
    pipeline=Pipeline([("polynomial_features",polynomial_features),("linear_regression",linear_regression)])#流水线
    return pipeline
from sklearn.metrics import mean_squared_error

degrees=[2,3,5,10]#多项式的阶数
results=[]#结果数组
for d in degrees:#运行四次
    model=polynomial_model(degree=d)#生产degree多项式模型
    model.fit(X,Y)#将X,Y扔到模型里面去训练
    train_score=model.score(X,Y)#得到评分
    mse=mean_squared_error(Y,model.predict(X))#计算均方根误差
    results.append({"model":model,"degree":d,"score":train_score,"mse":mse})#追加对应数据到results里面
for r in results:
    print("degree:{};train score:{};mean squared error:{}".format(r["degree"],r["score"],r["mse"]))
from matplotlib.figure import SubplotParams
plt.figure(figsize=(12,6),dpi=200,subplotpars=SubplotParams(hspace=0.3))
                  #subplotpars只是控制各下属图形高度上的间距为0.3
for i,r in enumerate(results):#循环四次
    fig=plt.subplot(2,2,i+1)#四张图，绘画顺序对应i+1
    plt.xlim(-2,9)#每张图的x轴的限制为-2到9，对应上面的x与y
    plt.title("LinearRegression degree={}".format(r["degree"]))#标题
    plt.scatter(X,Y,s=5,c='b',alpha=0.5)#蓝色的散点
    plt.plot(X,r["model"].predict(X),'r-')#预测的曲线

 ③算法结果

            

                                                             图1 不同阶级训练的准确度及误差

 

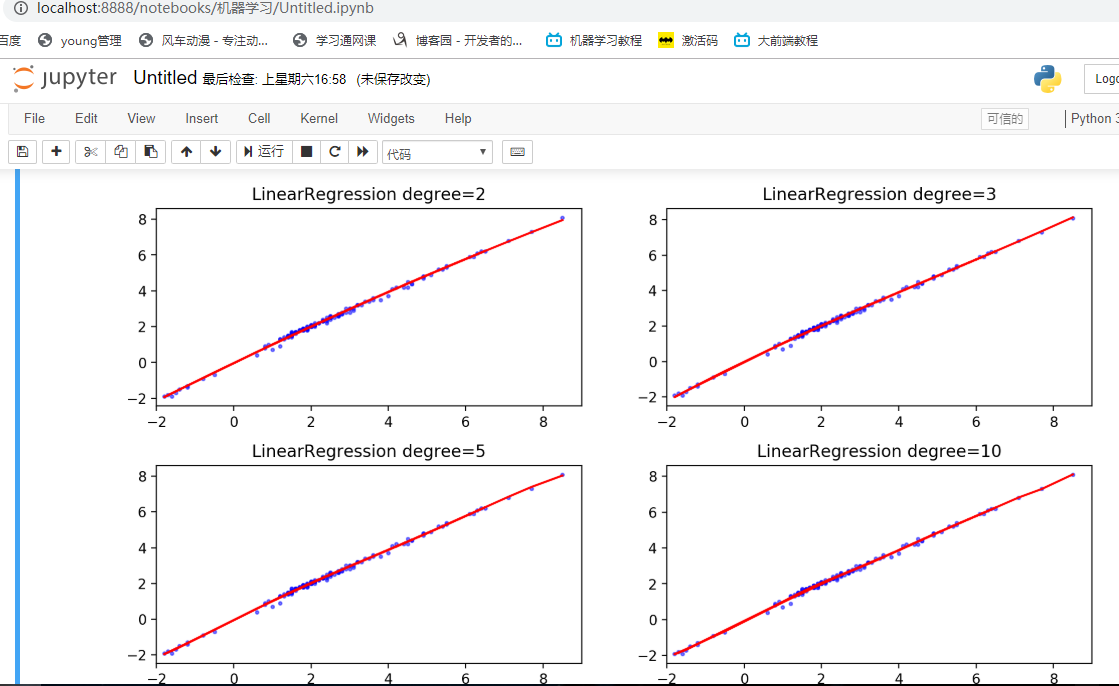
                                                                                     图2 训练结果可视化