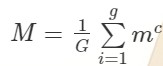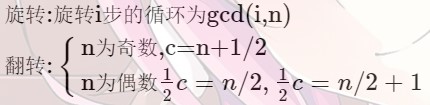置换群:G;置换群中置换个数:|G|;
我们喜欢用 m 阶循环这种记号来表示 置换。
m 阶循环:相邻元素可以直接到达,第 m 个位置可以到达第 1 个位置。
例如:5 阶循环:(1 5 2 4 3),1->5->2->4->3->1…..,3->4->2->5->1->3…..
前置技能还有:
共轭类格式:1^(c1) 2^(c2) … (n)^(cn),其中 cn 代表 n 阶置换的个数。
k 不动置换类(Zk):包含 k 的置换阶为 1
等价类(Ek):k 的轨迹
重要定理:|Ek||Zk| = |G|
Burnside 引理:群 G 是在这 n 个对象上用 m 种颜色进行染色后的方案集合上的置换群
不同等价类个数:L = sum{c1(ai)} / |G|, 1 <= i <= |G|; 其中 ai 是第 i 个置换
因为 sum{Zj} = sum{c1(ai)}, 1 <= j <= n, 1 <= i <= |G|; 其中 n 是置换对象个数
不同等价类个数还可以等于:L = sum{Zi} / |G|, 1 <= i <= n;
Polya 定理:群 G 是作用在 n 个对象上的置换群
不同等价类个数:L = sum{m^c(ai)} / |G|, 1 <= i <= |G|; 其中 c(ai) 为置换 ai 的循环节数(有多少个循环),一个置换对象有 m 种不同情况
区别和联系:
Polya 定理的群 G 是作用在 n 个对象上的置换群,相应地,Burnside 定理中的群 G 是在这 n 个对象上用 m 种颜色进行染色后的方案集合上的置换群。
Burnside 的 ai 和 Polya 的 ai 是不一样的,但是都是求在 ai 置换之后不变的染色方案数的和 / |G|,因为每种染色情况都重复出现了 |G| 次
Burnside 的 ai 作用下不变的图像 正好是对应着 Polya 的 ai 的循环节中的对象染以相同的颜色所得到的图像,所以 c1(ai) = m^c(ai)