[USACO4.2]草地排水Drainage Ditches

传送门

这个题几乎可以用来作为最大流入门的题了，没有任何掩饰，直接告诉你这是最大流。
这里解释一下网络流的建反向边操作，这其实是一个退流操作，拿下面一个图举个例子：

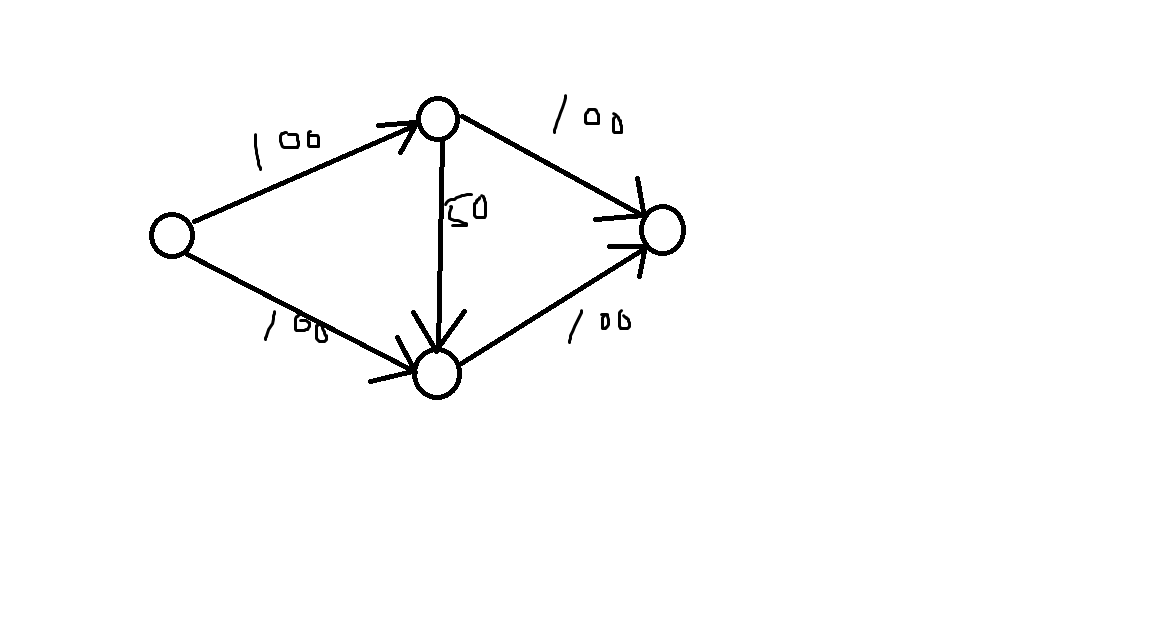
如果最先走了中间那条边，我们这个图就会变成这样：

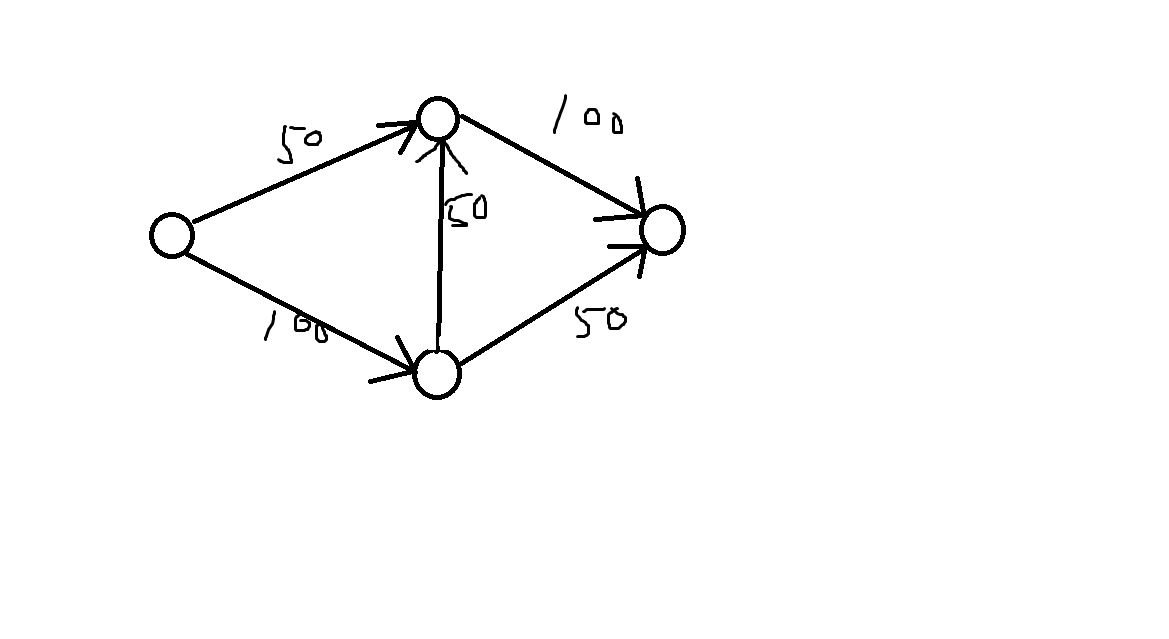
此时我们发现那条反向边能被另一条路径经过，但是这样不是错的吗，因为实际上这条路径是不存在的，让我们走走试试：

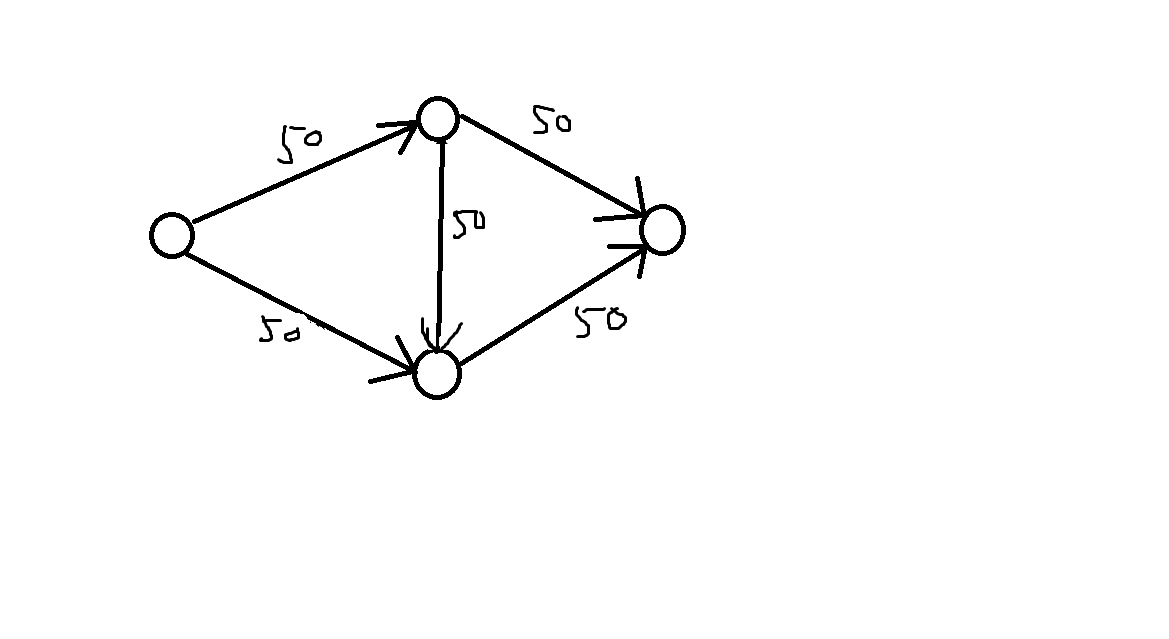
诶，这不就等价于上面那条路走掉了50流量，下面那条路也走掉了50流量，让我们再仔细思考一下：中间那条边的状态又和最初一样了，就好像没有走过。
所以反向边走掉多少流量就等于退回正向边多少流量，然后我们就能发现这个做法显然是正确的。
自我认为没有什么别的难理解的地方了。
代码（dinic）：

#include<cstdio>
#include<queue>
#include<cstring>
#define min(a,b) (a<b?a:b)
int dis[201],ans,n,m,cnt=1,s,t,inf=1e9+7,pre[401],nxt[401],h[201],v[401];std::queue<int>q;
void add(int x,int y,int z)
{
    pre[++cnt]=y,nxt[cnt]=h[x],h[x]=cnt,v[cnt]=z;
    pre[++cnt]=x,nxt[cnt]=h[y],h[y]=cnt;
}
bool bfs()
{
    memset(dis,0,sizeof dis);
    q.push(s),dis[s]=1;
    while(!q.empty())
    {
        int x=q.front();q.pop();
        for(int i=h[x];i;i=nxt[i])if(!dis[pre[i]]&&v[i])dis[pre[i]]=dis[x]+1,q.push(pre[i]);
    }
    return dis[t];
}
int dfs(int x,int flow)
{
    if(x==t||!flow)return flow;
    int f=flow;
    for(int i=h[x];i;i=nxt[i])
        if(v[i]&&dis[pre[i]]>dis[x])
        {
            int y=dfs(pre[i],min(v[i],f));
            f-=y,v[i]-=y,v[i^1]+=y;
            if(!f)return flow;
        }
    if(f==flow)dis[x]=-1;//这是一个优化，正确性显然 
    return flow-f;
}
int main()
{
    scanf("%d%d",&n,&m);s=1,t=m;
    for(int i=1,x,y,z;i<=n;i++)scanf("%d%d%d",&x,&y,&z),add(x,y,z);
    for(;bfs();ans+=dfs(s,inf));
    printf("%d
",ans);
}